Введение
Одной из ключевых задач современной биологии является изучение происхождения и функционирования сложных систем, в том числе и таких, развитие которых регулируется относительно простыми законами. Весьма высоким уровнем сложности обладает многоклеточный организм. Повышение сложности многоклеточного в ходе онтогенеза происходит постепенно в результате его развития из одной клетки.
Классическое представление о сложности в природе предусматривает рассмотрение нескольких общепринятых последовательных иерархических уровней организации. Первый уровень – это происхождение клетки, отграниченной от окружающей среды. Далее выделяется уровень эвкариотической клетки. Третий уровень сложности – это формирование многоклеточного организма. На следующем этапе многоклеточные организмы формируют популяции. Последний рассматриваемый биологами уровень сложности объединяет популяции в виды и сообщества, а сообщества в биосферу [2]. Данная работа является попыткой моделирования третьего уровня сложности биологических систем – уровня многоклеточных организмов. Сразу нужно заметить, что по причине сильного упрощения модели по сравнению с живой природой модель отвечает только задаче иллюстрации морфогенеза. Однако по причине модульного строения программы потенциальные возможности по её расширению ограничиваются только нашим знанием биологии.
Сразу нужно заметить, что по причине сильного упрощения модели по сравнению с живой природой модель отвечает только задаче иллюстрации морфогенеза. Однако благодаря модульному строению программы потенциальные возможности по её расширению ограничиваются только объемом имеющихся данных по механизмам индивидуального развития реальных организмов.
Клеточные автоматы – математические объекты с дискретными пространством и временем. Каждое положение в пространстве представлено отдельной клеткой, а каждый момент времени – дискретным временным шагом или поколением. Состояние каждого пространственного локуса или клетки определяется очень простыми правилами взаимодействия. Эти правила предписывают изменения состояния каждой клетки в следующем такте времени в ответ на текущее состояние соседних клеток. Впервые, идея таких автоматов отмечена в работах Неймана, когда он работал над идеей саморепродуцирующихся машин [31].
Модели клеточных автоматов используются в экологии и при моделировании эволюции. Примером экологической модели, работающей по принципу автоматов, является модель роста леса на месте пожарища [12]. В качестве элементарных ячеек рассмотрены экологические группы конкурирующих растений на вырубке – вейника и ростков березы. Для каждой ячейки задается степень конкуренции, а также закон перехода из одной экологической ячейки в другую. Функционирование каждой ячейки задается динамическим уравнением роста биомассы, для каждой группы свои параметры роста. Степень конкуренции и соответственно рост в каждой из ячеек зависит от состояния соседних ячеек. Модель параметризована на основе данных десятилетних оценок состояния конкретной вырубки. Эта модель хорошо описывает реальную картину зарастания вырубки и вытеснения травянистых растений молодыми проростками березы; также определены границы условий, при которых березняк вырастет, вне этих условий вырубка останется лугом.
Другой класс моделей с использованием принципа клеточных автоматов разрабатывался для описания заполнения экологических ниш. Одна из наиболее известных моделей с подобными задачами – это модель расселения гаммарид оз.Байкал [7]. В оз. Байкал эти ракообразные очень быстро эволюционировали и заняли несвойственные им экологические ниши, вплоть до глубоководных. В связи с этим была разработана модель, в которой элементарной ячейкой служила экологическая ниша с определенными вертикальными и горизонтальными границами и заданными ресурсами. Гаммариды определенной экологической ниши могли при заданных параметрах мутаций занять соседнюю нишу или могли вымереть. Мутации моделировались случайными числами в определенном диапазоне. Мутации меняли приспособленность, которая должна была соотноситься с ресурсами каждой ячейки. Если она была выше или равна ресурсам, то популяция выживала, если ниже, то вымирала. Если приспособленность удовлетворяла ресурсам соседней пустой ячейки, то «гаммариды» могли ее занять. Если она уже была занята, то сравнивались приспособленности конкурирующих популяций. При определенной разнице приспособленности, могло произойти вытеснение, и ячейка заполнялась популяцией с новыми параметрами. Эта модель хорошо описывала динамику расселения гаммарид по вертикали и современное распределение экологических групп.
В 2008 году была опубликована еще одна модель [8]. В этой работе описывалась имитационная модель эволюции одноклеточного животного в двухслойный организм, способный к независимому существованию. В модельном объекте формировались два слоя клеток; характерной чертой внутреннего из них была способность к секреции пищеварительных ферментов, расщеплению и всасыванию органических веществ. Эволюция таких модельных объектов сопровождалась мутациями, напоминающими реальные формы приспособлений у некоторых видов кишечнополостных и пластинчатых. Иногда наблюдалось появление во внешнем слое клеток, способных к секреции пищеварительных ферментов.
Модель «EvoDevo»
Из приведенного выше обзора становится ясно, что, несмотря на большое количество существующих моделей клеточных автоматов, всё еще остается слабо разработанной ниша клеточного автомата, ставящего перед собой задачу моделирования индивидуального развития многоклеточного существа.
В данной работе предложен метод моделирования онтогенеза и программа, его реализующая. Модель во многом основана на известных реалиях биологии развития и функционирования клетки.
В основу модели заложены следующие положения:
1. В моделируемом пространстве все клетки равноправны. Они занимают одинаковый объем, имеют одинаковую форму и одинаковый набор свойств («правил поведения»).
2. Взаимодействие между клетками осуществляется посредством сигнальных веществ, либо через непосредственный контакт. Но в случае непосредственного контакта учитывается только количество соседних клеток.
3. В модели должно существовать пространство для случайных событий.
Следует заметить, что эти постулаты хотя и вносят серьезные ограничения в возможности моделирования «биологически достоверных» объектов, имеют под собой серьезную базу. Первый пункт соответствует тому, что обычно наблюдается на ранних стадиях развития многоклеточных животных: все клетки зародыша (бластомеры) исходно «равноправны» и имеют одну и ту же изначально заложенную «программу поведения». Второй пункт также соответствует имеющимся данным о механизмах онтогенеза многоклеточных, в ходе которого клетки развивающегося зародыша обмениваются информацией (в том числе сигналами, модулирующими поведение других клеток). Средcтвами коммуникации являются химические сигналы и физический контакт [11]. Третий пункт не только соответствует биологической реальности, но и обязателен для каждой биологической системы. Но, несмотря на узаконенную случайность, в рамках модели, как будет показано ниже, возможно создание устойчивых структур.
Модель состоит из трех основных независимых компонентов: игровое поле, набор клеток и набор правил. Игровое поле представляет из себя набор ячеек шестиугольной формы, обладающих определенными свойствами, и набор констант, характеризующих окружающую среду
Коммуникация между клетками осуществляется с помощью «химических» сигналов. Каждая из ячеек игрового поля является потенциальным носителем сигнального вещества, необходимого для поддержания связи (химической коммуникации) между клетками. Предусмотрено три типа сигнальных вещества с различным свойствами. Сигнальные вещества первого типа свободно распростаняются по полю свободно проникая сквозь преграды в виде клеток. Вещества второго типа распространяются только по незянятым ячейкам "игрового поля", позволяя моделировать образование вакуолей. Вещества третьего типа распространяются только от клетки к клетке, что позволяет моделировать распространение сигналов по нервным волокнам. Все сигнальные вещества обладают свойством пониженной устойчивости.
При моделировании различных многоклеточных образований в нашей модели часто возникают ситуации, когда клетке необходимо совершить некое направленное действие (например, переместиться по градиенту концентрации сигнального вещества в среде). В связи с этим встает задача определения градиента функции, дискретной и по значению, и по обоим аргументам. Концентрация сигнального вещества максимальна в поле, занимаемом выделяющей его клеткой. В точке максимума все частные производные равны нулю. Следовательно, при необходимости выбора направления клеточного деления в сторону уменьшения концентрации сигнального вещества клеткой будет руководить исключительно случайность. Кроме того игровое поле характеризуется «плотностью среды». Этот параметр моделирует снижение концентрации сигнальных веществ в зависимости от расстояния.
Клетка представляет из себя программную единицу нашей модели, описываемую набором параметров, так или иначе связанных с взаимодействием клетки с окружающей средой. В модели жестко задано, что ни одна клетка не может занимать поле, уже занятое другой клеткой. Остальные параметры заданы модульно.
Первый параметр – уровень выделения. Это число, определяющее количество сигнального вещества, выделяемого в среду при условии, что клетка производит выделение. Численно уровень выделения равен количеству вещества в точке экстремума. Варьируя этот параметр и проницаемость среды можно добиться различных форм графиков распределения сигнального вещества в пространстве.
Второй параметр - чувствительность рецепторов. Этот параметр определяет способность клетки реагировать на присутствие в среде сигнального вещества. В нашей модели уровень возбужденности рецепторов вычисляется по формул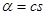е 
, где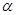 
- степень возбужденности рецепторов, с – концентрация сигнального вещества в ячейке, в которой расположена клетка, s - чувствительность рецепторов, причем 
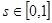. При s=0 рецепторы вообще не реагируют на данное вещество. При s=1 степень реакции (степень возбужденности рецепторов) численно равна концентрации сигнального вещества в данной точке.
Третий параметр – количество соседей. Этот параметр напоминает нам модель, предложенную в 1970 году Джоном Конвеем. Количество клеток-соседей в биологии может являться параметром, связанным обратной зависимостью со степенью контакта клетки с окружающей средой и, соответственно, со степенью доступа к ресурсам окружающей среды, таким как кислород, питательные вещества и др.
И, наконец, третьим важным компонентом модели является программа поведения клетки. Она представляет из себя набор инструкций, составленных согласно установленному синтаксису. Данная программа является общей для всех клеток и выполняеется для каждой клетки при каждой итерации по дискретному времени.
Программная реализация. Описание программы EvoDevo.exe
В процессе работы над данным проектом была разработана программа, являющая собой реализацию описанной выше модели. Программная реализация, в отличие от теоретической модели, имеет несколько ограничений, связанных с физическими возможностями современных вычислительных систем, а также с ограничениями языка программирования.
Программа получила название «EvoDevo», что является сокращением от английского «evolution of development» то есть «эволюция развития». Это отдельная ветвь биологии, занимающаяся изучением эволюции механизмов индивидуального развития организмов, а также обратного влияния законов индивидуального развития на эволюционный процесс [30]. Одной из основных целей данного направления исследований является изучение генетических механизмов регуляции индивидуального развития (напомним, что в нашей модели аналогом генома является набор правил поведения клетки). В частности, биологи установили, что реализация похожих «генетических программ» порой приводит к формированию сильно различающихся морфологических структур (фенотипических признаков), в то время как похожие фенотипические признаки иногда развиваются на основе сильно различающихся «генетических программ» [19].
Это свидетельствует об очень сложном, нелинейном характере соотношения между генотипом (набором «правил поведения» клетки) и строением взрослого организма. В ходе индивидуального развития фенотип формируется посредством сложных процессов самоорганизации, в ходе которых сложные структуры образуются в результате взаимодействия и информационного обмена между множеством делящихся клеток, каждая из которых изначально имеет одну и ту же «программу поведения» (геном). Наша модель разрабатывалась как инструмент, помогающий лучше понять природу и закономерности этих процессов самоорганизации, которые часто приводят к неожиданным и, на первый взгляд, труднообъяснимым результатам.
Перед тем, как мы приступим к рассмотрению примеров работы программы необходимо обратить внимание на одну важную особенность. Дело в том, что в ходе работы программы довольно часто возникают ситуации, когда выбор дальнейшего пути развития определяется случайностью. Поэтому для одного и того же набора правил порой могут получаться совершенно разные результаты. При этом обычно для одного и того же набора правил существует конечный набор более или менее дискретных вариантов итогового «фенотипа». Такая ситуация хорошо соответствует фактическим данным по онтогенезу многоклеточных организмов. Некоторые авторы используют для описания онтогенеза образ холмистого ландшафта с системой ветвящихся борозд или оврагов. Развивающийся организм представляется в виде шарика, катящегося по этим оврагам. Обычно шарик выбирает самый глубокий из оврагов и приходит к одному и тому же конечному результату (фенотипу), однако различные возмущения (внутренние – мутации, или внешние – резкие изменения условий, в которых происходит развитие организма) могут привести к тому, что шарик перейдет в один из второстепенных оврагов, и в итоге сформируется аберрантный (уклоняющийся от «нормы») фенотип [14].
Для всех рассмотренных ниже примеров начальное состояние моделируемой системы одно и то же. На неограниченном игровом поле находится единственная клетка, являющаяся центром дальнейшего развития. Все правила составлены с расчетом на эту единственную исходную клетку. При моделировании многоклеточных организмов эта клетка соответствует зиготе (оплодотворенной яйцеклетке), при моделировании популяций одноклеточных организмов – организму–«основателю».
Моделирование простейших нитчатых структур.
Начнем с простейшего примера. Нитевидные многоклеточные структуры достаточно часто встречаются в природе (нитчатые бактерии, нитчатые водоросли, мицелий грибов). В нашей модели для того, чтобы смоделировать нитевидную структуру, достаточно следующей генетической программы:
if (cell.sensorReaction[0]<0.1) { cell.Secret(0); }
if (cell.neighboursCount<2) { cell.SpawnWhereLess(0); }
В результате исходная клетка мгновенно начинает выделение сигнального вещества и делится. Теперь для каждой из двух клеток активно лишь второе правило, следовательно, каждая из них поделится еще раз. Теперь для двух внутренних клеток не осталось ни одного активного правила, а для внешних клеток активным является второе правило. Происходит дальнейшее наращивание нити в обе стороны до тех пор, пока для концевой клетки не станет активным первое правило. В этот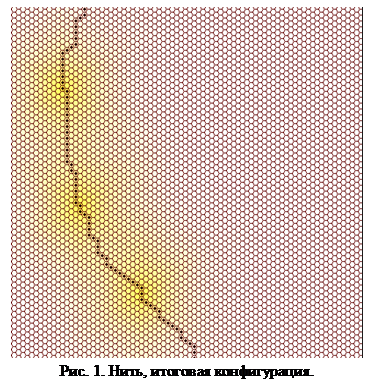 
момент концевая клетка нити начнет выделение сигнального вещества, что позволит нити расти далее. Цикл повторяется до тех пор, пока растущая нить не встретит какого-нибудь механического препятствия. Результат работы модели с заданными правилами показан на рис. 1.
Таким образом, с помощью рассматриваемой модели нам удалось смоделировать простейший многоклеточный «организм» имеющий, тем не менее, определенное сходство с реальными живыми организмами, особенно с нитчатыми цианобактериями. У модельного организма два типа клеток: выделяющие и не выделяющие, причем первые располагаются через примерно равные промежутки. Точно так же в нитях многих нитчатых цианобактерий располагаются специализированные клетки – гетероцисты, функция которых состоит в фиксации атмосферного азота и синтезе азотистых соединений, используемых всеми клетками нити. Гетероцисты выделяют сигнальное вещество, препятствующее превращению соседних клеток в гетероцисты [34].Так же и в нашей модели вещество, выделяемое специализированными (выделяющими) клетками, не позволяет соседним клеткам стать выделяющими.
Моделирование сложных нитчатых структур. Модель «Мицелий».
По сути, мицелий является разветвленной нитчатой сетью. Следовательно, для его моделирования необходимо изменить набор правил так, чтобы нить ветвилась через некоторые промежутки. Для этого был разработан следующая программа:
if (cell.sensorReaction[0]<0.1) cell.Secret(0);
if (cell.neighboursCount<2) cell.SpawnWhereLess(0);
else
if (cell.neighboursCount<3 && cell.sensorReaction[0]>0.4) сell.SpawnWhereLess(0);
Согласно этим правилам, исходная клетка начинает выделять сигнальное вещество. Далее отростки начинаю вести себя подобно нити из предыдущего примера. Это продолжается вплоть до того момента, когда снова активизируется первое правило, и начинается выделение. В тот момент, когда началось выделение сигнального вещества, второе правило стало активным для всех близлежащих клеток. Образовалась вторая зона активного деления. Так будет продолжаться до тех пор, пока разрастающаяся сетка мицелия не заполнит все предоставляемое ей пространство. Пример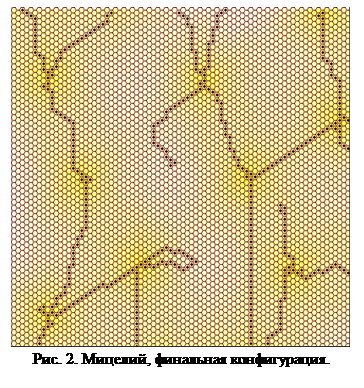 
финальной конфигурации показан на рис. 2.
Следует обратить внимание, что не все области выделения становятся точками расхождения ветвей. В некоторых случаях образуются стабильные структуры. Однако вероятность образования устойчивой структуры не превосходит вероятности ветвления, а, следовательно, при достаточно развитой сети мицелия вероятность самопроизвольного прекращения развития весьма мала.
Моделирование образования сложной осевой симметрии. Модель «Червяк».
Предыдущий пример ставил перед собой цель продемонстрировать возможность моделирования осевой симметрии, не более того. Теперь попытаемся использовать результат, полученный в предыдущем примере, для моделирования более сложной структуры, условно названной «Червяк»
Используемая программа достаточно сложна для понимания. Её логическая идея заключается в образовании центра деления, выделяющего сигнальное вещество. При этом близлежащие клетки начинают делиться невзирая на количество соседей, а когда вокруг центра деления остается только одна свободная ячейка он перемещается. Когда он становится слишком удален от исходной клетки начинается выделение игнибитора роста, сочетание которого с головным веществом вызывает появление отростков. Посмотрим, однако, каким образом происходит развитие моделируемого организма в данном случае.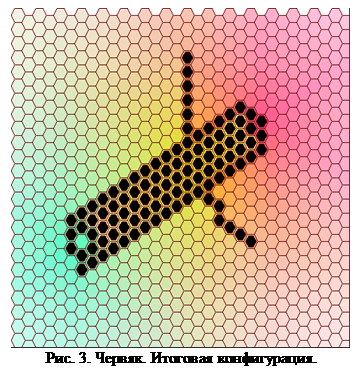 
Как мы видим на рис 3, образовалась многоклеточная структура, обладающая осевой симметрией и продольной дифференциацией «отделов тела». Попытаемся теперь внести небольшие изменения в набор правил («мутацию»). Для отростков понизим порог сигнального вещества, необходимого для роста. По изначальной идее это должно было просто удлинить отростки, однако эффект неожиданно оказался значительно более сильным и многоплановым.
Вначале развитие организма идет тем же путем, что и без мутации, однако когда дело доходит до роста конечностей появляется непредвиденный эффект. Да, сначала действительно «щупальца» просто растут в длину. Однако, когда конечности вырастают достаточно длинными, они начинают препятствовать доступу сигнального вещества, выделяемого хвостовым центром, к передней части туловища. Ингибирующее действие хвостового вещества прекращается, и рост переднего конца тела возобновляется. При этом отростки всё удлиняются, и в какой-то момент на них образуются новые центры выделения первого (головного) сигнального вещества.
Рост головного конца продолжается до тех пор, пока он не удалится на достаточное расстояние от конечностей. В какой-то момент образуется новый центр выделения хвостового вещества, но уже не на хвосте, а ближе к голове, ингибируя рост головного сегмента. Этим, впрочем, странности не ограничиваются. В 7% случаев головное вещество, образовавшееся на конечностях, оказывает влияние на растущий головной конец, искривляя его и заставляя изменить направление роста. Из подобных результатов небольшого изменения «генотипа» (набора правил поведения клетки) следует множество интересных выводов, на которые хотелось бы обратить внимание.
Как мы видим, изменение одного, на первый взгляд малозначительного параметра, несущего, кроме того, строго определенную функцию (исходно он определял только длину конечностей), повлекло за собой изменение целого ряда параметров итоговой многоклеточной структуры, не связанных с тем, что мы пытались изменить. Таким образом, мы получили наглядную демонстрацию того, что в нашем примере невозможно удлинение конечностей, не влияющее на всю структуру в целом. Это соответствует представлениям биологов о «морфогенетических корреляциях», то есть о тесной взаимосвязи различных частей развивающегося эмбриона, благодаря которым изменение одной части может оказать существенное влияние на развитие других частей [15].
Отсюда также следует предположение о том, что функции белков – регуляторов онтогенеза могут быть множественными. Мы попытались изменить один, казалось бы, узкоспециализированный «белок-регулятор», и в результате обнаружили, что он на самом деле способен влиять не только на длину конечностей, но и на длину «туловища», его форму, стимулировать образование дополнительных выростов и даже нарушать осевую симметрию (имеется в виду пятно выделения сигнального вещества на «боку», а также возникающее в некоторых случаях искривление туловища). Всё это позволяет допустить проведение аналогии между некоторыми свойствами правил нашей модели и функциями белков-регуляторов в эмбриогенезе. Развитие этой гипотезы – тема для отдельного исследования, однако следует отметить, что из биологии известны примеры, когда мутация одного-единственного гена – регулятора онтогенеза может приводить к множественным неожиданным эффектам. Например, мутация одного из таких генов у дрозофилы приводит к формированию эмбриона, покрытого многочисленными мелкими отростками, из-за чего этот ген получил название hedgehog [32].
Теперь рассмотрим другое небезынтересное предположение, которое можно выдвинуть на основании рассмотренного выше примера. В настоящее время выдвинуто множество гипотез, пытающихся объяснить так называемый «кембрийский взрыв» - относительно внезапное (в геологическом масштабе времени) увеличение разнообразия животных, произошедшее в позднем венде и раннем кембрии. В этот период в палеонтологической летописи впервые появляются почти все существующие доныне типы животных [10]. Существует множество гипотез, стремящихся объяснить это явление. Его пытаются связать с ростом концентрации кислорода, с глобальным оледенением в позднем неопротерозое, с изменениями состава морской воды, с разными другими биотическими и абиотическими факторами [3]. Рассмотренный выше пример позволяет предложить еще одну гипотезу для объяснения «кембрийского взрыва».
Как было показано выше, даже небольшой мутации может оказаться достаточно для образования большого количества различных «вариаций на тему» исходного «существа». Иными словами, моделируемая система эмбриогенеза двусторонне-симметричного существа с минимальным набором «дополнительных органов» (в нашем случае – с одной парой придатков-щупалец) обладает высокой нестабильностью. Разумеется, в результате естественного отбора процесс эмбриогенеза должен постепенно стабилизироваться [14]. Должны постепенно появляться дублирующие регуляторные системы, большое количество отрицательных обратных связей и тому подобное. Однако на ранних этапах становления двусторонне-симметричного плана строения и, как следствие, сложного эмбриогенеза, согласно нашей модели, онтогенетическая система могла оказаться нестабильной, что вело, с одной стороны, к высокой смертности, а с другой – высокому разнообразию фенотипов, получающихся в результате реализации одной и той же «генетической программы развития».
Можно предположить, что именно в этот период и было заполнено все «пространство логических возможностей», предоставляемое двусторонне-симметричной организацией, и, соответственно, появились все возможные типы двусторонне-симметричных животных. После взрывообразной диверсификации начался медленный процесс стабилизации. Согласно результатам работы предлагаемой модели можно предположить, что процесс стабилизации гораздо более ресурсоемкий, чем процесс увеличения разнообразия, что объясняет большие затраты времени. Данное предположение косвенно подтверждается известным палеонтологам правилом «архаического многообразия», согласно которому на ранних этапах эволюции крупных групп организмов (типов, классов) часто наблюдается очень высокое разнообразие планов строения, причем варьируют в том числе и такие признаки, которые в ходе дальнейшей эволюции перестают варьировать и становятся устойчивой характеристикой тех или иных эволюционных линий и групп организмов [6].
К слову, нестабильность некоторых простых систем индивидуального развития позволяет также выдвинуть предположение, объясняющее такие странные находки, как хайнаньская биота [4]. Подтверждение либо опровержение выдвинутой гипотезы – тема для дальнейших исследований.
Заключение и выводы
Осталось подвести финальную черту, суммируя всё вышесказанное.
В работе была предложена модель, существенно отличающаяся от своих предшественниц. Изначально модель предназначалась как метод моделирования онтогенеза, но впоследствии появились предпосылки для её использования и в других целях. Главное достоинство модели, по-видимому, состоит в том, что она позволяет изучать разнообразные трудно предсказуемые процессы самоорганизации, основанные на взаимодействии множества объектов, каждый из которых изначально имеет одну и ту же «программу поведения» (подчиняется одному и тому же набору правил). Подобные процессы широко распространены в живой природе, однако наука еще далека от полного понимания таких процессов.
Были построены симуляции развития некоторых живых организмов, на основе которых были выдвинуты гипотезы о причинах «кембрийского взрыва»; о возможных множественных последствиях небольших изменений (мутаций) генов – регуляторов онтогенеза многоклеточных или социального поведения одноклеточных; о причинах множественности и сцепленности функций белков в эмбриогенезе. Была построена модель общественного поведения одноклеточных, имеющая некоторую схожесть с общественным поведением бактерий и миксамеб.
Разумеется, работу над данной моделью ни в коем случае нельзя считать завершенной. Уже на данном этапе намечаются дальнейшие пути развития, способные занять не один год. Так, например, для моделирования сложных организмов целесообразно ввести такое понятие, как группы правил. Это позволит использовать модульный принцип при моделировании онтогенеза. В реальном эмбриогенезе существует явление одновременной активизации целых групп генов при определенных условиях. На этом основан принцип работы Hox-генов, от которых зависит дифференцировка отделов тела двусторонне-симметричных животных вдоль передне-задней оси: например, один Hox-ген включает группу генов, необходимых для превращения данного сегмента эмбриона в голову, другой аналогичным образом инициирует превращение другой части эмбриона в грудь, хвост и т.д. [28]
Реализация подобного механизма регуляции онтогенеза в нашей модели возможна, если для каждой группы правил для каждой клетки будет установлен наследуемый флаг активности, который сможет изменяться в зависимости от внешних сигналов. Это позволит моделировать сложные процессы дифференциации клеток, развитие тканей и внутренних органов, иными словами, это обеспечит возможность моделирования более сложных и структурированных организмов.
Кроме того, существенным недостатком модели является невозможность более тонких и индивидуализированных взаимодействий между клетками. Невозможна передача индивидуального сигнала непосредственно от одной клетки к другой через межклеточный контакт. Невозможно движение всего организма и многое другое, попадающее под термин «сцепленное взаимодействие».
Перечисленные изменения позволят существенно приблизить получаемые результаты к тому, что можно наблюдать в живой природе, но уже на данном уровне развития модели она, по-видимому, представляет собой интересный инструмент для исследования процессов самоорганизации в биологических системах, позволяющий выдвигать и тестировать различные гипотезы, затрагивающие важные аспекты современной науки.
Литература:
1. Гарднер М. Крестики-нолики. М.: Мир, 1988.
2. Гринченко С.Н. Системная память живого (как основа его метаэволюции и периодической структуры). М.: Мир, ИПИРАН, 2004.
3. Еськов К.Ю. История Земли и жизни на ней. М.: МИРОС - МАИК "Наука/Интерпериодика", 2000.
4. Еськов К.Ю. «Черновики Господа Бога» // Знание-Сила. 2001. № 6.
5. Колчанов Н.А., Суслов В.В., Гунбин К.В. Моделирование биологической эволюции: регуляторные генетические системы и кодирование сложности биологической организации // Вестник ВОГиС. 2004. Т. 8. №2. С. 86-99.
6. Мамкаев Ю.В. Методы и закономерности эволюционной морфологии // Современная эволюционная морфология / ВоробьеваЭ.И., Вронский А.А. (ред.). Киев: Наукова Думка, 1991. С. 88-103.
7. Меншуткин В. В., Ащепкова Л. Я. Моделирование процесса эволюции байкальских гаммарид // Долгосрочное прогнозирование состояния экосистем. Новосибирск, 1988, с. 198-214.
8. Меншуткин В.В., Наточин Ю.В. Имитационное моделирование процесса образования многоклеточных животных. Палеонтологический журнал - № 2, Март-Апрель 2008, С. 3-12
9. Ратнер В.А. Внешние и внутренние факторы и ограничения молекулярной эволюции. В кн.: Современные проблемы теории эволюции (ред. Л.П.Татаринов). М.: Наука, 1993.
10. Розанов А.Ю. Что произошло 600 миллионов лет назад. М.: Наука, 1986.
11. Рэфф Р., Кофмен Т. Эмбрионы, гены и эволюция. М.: Мир, 1986.
12. Уланова Н.Г., Белова И.Н., Логофет Д.О. О конкуренции среди популяций с дискретной структурой: матричная модель динамики популяций вейника и березы, растущих совместно // Журнал общей биологии. 2008. Т. 69. № 6. С. 441-457.
13. Уоддингтон К.Х. Основные биологические концепции. В кн.: На пути к теоретической биологии. I. Пролегомены. — М.: Мир, 1970. С. 11–38.
14. Шишкин М.А. Закономерности эволюции онтогенеза. В кн.: Современная палеонтология. М.: Недра, 1988. Т.2. С.169-209.
15. Шмальгаузен И.И. Организм как целое в индивидуальном и историческом развитии. М.: Наука, 1982.
16. Arbib M. A. Theories of Abstract Automata. - Prentice-Hall, 1969.
17. Bak P., Tang C., Wiesenfeld K. (1988). Self-organized criticality // Physical Review A 38: 364–374.
18. Bischoff B., Schnabel R. A Posterior Centre Establishes and Maintains Polarity of the Caenorhabditis elegans Embryo by a Wnt-Dependent Relay Mechanism // PLoS Biology. 2006. 4(12): e396.
19. Cañestro C., Yokoi H., Postlethwait J.H. Evolutionary developmental biology and genomics // Nat Rev Genet. 2007. V. 8. P. 932-942.
20. Cartwright H.N., Humphries J.A., Smith L.G. PAN1: A Receptor-Like Protein That Promotes Polarization of an Asymmetric Cell Division in Maize // Science. 2009. V. 323. P. 649–652.
21. Chen Y, Zhao X. Shaping limbs by apoptosis // J Exp Zool. 1998. V. 282. P. 691-702.
22. Conway's Game of Life. - IBM Research Report RC 6802, October 1977.
23. Daniels R, Vanderleyden J, Michiels J. Quorum sensing and swarming migration in bacteria // FEMS Microbiol Rev. 2004 Jun;28(3):261-89.
24. Ellermeier C.D., Hobbs E.C., Gonzalez-Pastor J.E., Losick R. A Three-Protein Signaling Pathway Governing Immunity to a Bacterial Cannibalism Toxin // Cell. 2006. 124, 549–559.
25. Fiegna F., Yu Y.-T. N., Kadam S. V., Velicer G. J. Evolution of an obligate social cheater to a superior cooperator // Nature. 2006. V. 441. P. 310-314.
26. Getling A.V., Brausch O. Cellular flow patterns and their evolutionary scenarios in three-dimensional Rayleigh-Benard convection // Physical Review. 2003. E 67: 046313.
27. Langton C. Studying Artificial Life with Cellular Automata // Physica D 22. 1986. P. 120-149.
28. Lemons D., McGinnis W. Genomic Evolution of Hox Gene Clusters // Science. 2006. V. 313. P. 1912-1922.
29. La Scola B. et al. The virophage as a unique parasite of the giant mimivirus // Nature. 2008. V. 455. P. 100–104.
30. Müller G.B. Evo-devo: extending the evolutionary synthesis // Nat Rev Genet. 2007. V. 12. P. 943-949.
31. Neumann J. V. Theory of Self-Replicating Automata. - University of Illinois Press, 1966.
32. Nusslein-Volhard C., Wieschaus E. Mutations affecting segment number and polarity in Drosophila // Nature. 1980. V. 287. P. 795-801.
33. Wolfram S. "Statistical mechanics of cellular automata". Rev. Mod. Phys. 1983. V. 55. P. 601–644.
34. Zhang C.C., Laurent S., Sakr S., Peng L., Bédu S. Heterocyst differentiation and pattern formation in cyanobacteria: a chorus of signals. // Mol Microbiol. 2006. V. 59. P. 367-375.
