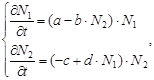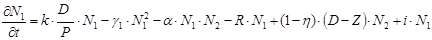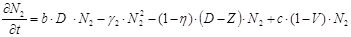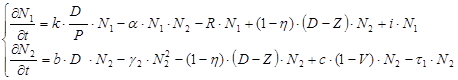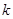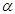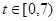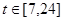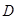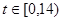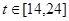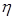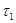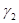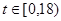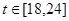Введение
Развитие мирового сообщества наглядно демонстрирует, что в последнее время критически важным государственным ресурсом, оказывающим все большее влияние на национальную безопасность, становится информация, циркулирующая в автоматизированных системах управления и связи. Ускоренное развитие информационных технологий открыло дополнительные возможности для преднамеренного деструктивного воздействия на них противостоящей стороны.
В отношении теоретических проблем исследования информационной войны, которую можно рассматривать как крайний способ разрешения противоречий в информационном обществе, согласно [1] выделяют следующие проблемы: недостаточно проработаны научные подходы и предложения по способам представления внутренней структуры тайной информационно-психологической операции, а так же методики аналитической реконструкции замысла, целей, задач, этапов, внутренней структуры тайных операций информационно-психологической войны по их признакам, внешним (доступным наблюдателю) следам и проявлениям.
Исследование процессов информационного противоборства так же рождает такие вопросы: «Какова общая картина поведения сторон, в каком конечном состоянии окажется данное сообщество, если известно его состояние на текущий момент времени? Как предсказать поведение системы информационного противоборства? Как выяснить влияние различных параметров системы информационного противоборства на ее динамику?». Для ответа на эти и многие другие вопросы проводятся исследования в области информационного противоборства сторон, разрабатываются математические модели противоборствующих сторон. Научным сообществом ведутся исследования в области моделирования информационных противоборств, а именно: разработка технологии имитационного моделирования процессов информационного противоборства [2], разработка многоагентной модели для исследования противоборства службы безопасности и ассоциации злоумышленников [3], разработка модели динамики противоборства неоднородных группировок сил [4], моделирование вооруженного противоборства [5], разработка агрегированной модели противоборства боевых систем [6], разработка модели информационного противоборства в социальной сети [7].
В данной статье представлен один из вариантов математических моделей противоборств, разработанный на основании гипотез математической теории популяций, математических моделей «хищник-жертва» В. Вольтерра и математической модели сражения Ланкастера, а именно математическая модель противоборств «Защитник информационных ресурсов – нарушитель».
Математическая модель противоборств
Рассмотрим базовую математическую модель противоборства В. Вольтерра, содержащую два вида, один вид – хищник, а другой их добыча. Пусть N1 и N2 - популяции жертв и хищников соответственно. Согласно предположениям из [9] рассмотрим динамику популяций, описываемую следующей системой дифференциальных уравнений:
|
|
(1) |
где а > 0 - скорость размножения при отсутствии хищников; с > 0 - интенсивность вымирания хищников в отсутствие жертв; b > 0 - коэффициент потери биомассы жертв хищников; d > 0 - коэффициент увеличения биомассы хищников в случае удачной охоты (чем больше жертв, тем больше биомасса хищников).
Проводя аналогию с описанием базовой модели для разработки моделей информационного противоборства получим такой подход, что в роли жертв выступают нарушители, а в роли хищников выступают защитники информационных ресурсов, это предположение обосновано тем фактом, что нарушители и защитники противостоят в сфере ИТ, где действия нарушителей направлены на получение доступа к информационным ресурсам, а действия защитников направлены на предотвращения несанкционированного доступа к информации и ликвидации источника такого воздействия.
Рассмотрим математическую модель противоборств «Защитник информационных ресурсов – нарушитель», которая отражает процессы присущие противоборству в сфере ИТ между защитниками информации и нарушителями в зависимости от социально-экономических условий в исследуемом регионе страны. После изучения предметной области информационного противоборства в сфере ИТ, выдвижения гипотез и проведения эмпирических исследований были определены факторы, которые влияют на численность противоборствующих сторон. Численность нарушителей зависит от следующих факторов:
1) рост числа нарушителей неизбежен, если доходы от преступных операций (D) превышают расходы на подготовку и проведение операций по несанкционированному доступу к информации (P), единицей измерения этих параметров являются рубли за единицу модельного времени (неделя, месяц, квартал), D ≥ 0, P ≥ 0;
2) уровень конкуренции (γ1) между нарушителями за общий информационный ресурс сдерживает прирост их численности, данный параметр измеряется в следующем диапазоне 0£ γ1 £1;
3) коэффициент (R) отражает строгость законодательства – риски, связанные с поимкой нарушителя (административное, уголовное наказание). Данный фактор должен сдерживать прирост нарушителей, т.к. возможность попасть в тюрьму будут останавливать потенциальных нарушителей от совершения преступлений. 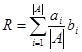 , где R ≥ 0, А – множество мер ответственностей по каждой статье уголовного и административного кодексов за нарушения в сфере ИТ,
, где R ≥ 0, А – множество мер ответственностей по каждой статье уголовного и административного кодексов за нарушения в сфере ИТ, 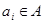 , a = min – условный срок, a = max – пожизненное заключение,
, a = min – условный срок, a = max – пожизненное заключение, 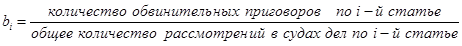 ;
;
4) качество подготовки специалистов по защите информационных ресурсов. Коэффициент качества подготовки защитников (α, измеряется в следующем диапазоне 0£ α £1) состоит из следующих основных компонент: качество полученного основного образования в ВУЗе, оценить которое возможно по среднему баллу во время обучения или по специальным тестам; периодичность и качество прохождения повышение квалификации, прохождения курсов по современным информационным технологиям и продуктам по защите информации, оценить которое возможно по среднему баллу во время обучения или по специальным тестам.
5) уровень общедоступности информации в глобальной сети Интернет (i) – в связи с ростом информационных ресурсов и возможностей глобальной сети (возможности получения сведений об угрозах безопасности, методов, способов и инструментария по реализации этих угроз), совершить информационные преступления становится все проще, что вызывает увеличение числа нарушителей, следовательно и рост компьютерной преступности. Данный параметр измеряется в следующем диапазоне 0£ i £1.
После определения факторов влияющих на численность нарушителей получим следующее дифференциальное уравнение:
|
|
(2) |
где k – нормирующий коэффициент (0£ k £1).
Численность защитников информации зависит от следующих факторов:
1) уровень потерь общества, понесенный в результате преступного нападения, то есть чем больше убытков несет общество от преступлений нарушителей, тем больше денег оно готово вкладывать в защитников информации (Z – затраты общества на содержание защитников, единицей измерения являются рубли за единицу модельного времени (неделя, месяц, квартал), Z ≥ 0);
2) уровень полезности защитников, который примем как частное от деления числа раскрытых компьютерных преступлений к общему числу совершенных преступлений. Данный параметр измеряется в следующем диапазоне 0£ V £1;
3) уровень нравственного здоровья общества, влияющий на переход защитников на сторону нарушителей (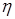 ), чем выше этот уровень, тем меньше таких переходов (основываясь на подходах количественной оценки и влияния данного параметра на процессы протекающие в обществе [10, 11, 12]);
), чем выше этот уровень, тем меньше таких переходов (основываясь на подходах количественной оценки и влияния данного параметра на процессы протекающие в обществе [10, 11, 12]);
4) конкуренция (γ2) между защитниками может сдерживать прирост их численности, данный параметр измеряется в следующем диапазоне 0£ γ2 £1;
После определения факторов влияющих на численность защитников получим следующее дифференциальное уравнение:
|
|
(3) |
где b, с - нормирующие коэффициенты (0£ b £1, 0£ c £1).
Численность нарушителей может увеличиваться за счет защитников информации. Если доходы злоумышленника от правонарушений D будут заметно превышать затраты общества на подготовку и содержание защитников Z, то последние начнут переходить (перепрофилироваться) на сторону нарушителей, в противном случае они будут противодействовать росту числа нарушителей.
Определим малозначительные факторы и внесем завершающие изменения в модель:
1) учитывая скрытный характер деятельности нарушителей и отсутствие взаимодействий между ними, исключим из модели уровень конкуренции γ1 между нарушителями;
2) введем коэффициент 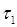 – интенсивность естественного сокращения защитников информации в случае отсутствия в них потребности, данный параметр измеряется в следующем диапазоне 0£
– интенсивность естественного сокращения защитников информации в случае отсутствия в них потребности, данный параметр измеряется в следующем диапазоне 0£ 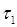 £1.
£1.
После определения факторов, которые влияют на численность противоборствующих двух сторон, получим для проведения дальнейших исследований систему двух дифференциальных уравнений:
|
|
(4) |
Математическая модель противоборств «Защитник информационных ресурсов – нарушитель» была исследована на устойчивость, также были проведены вычислительные эксперименты, подтвердившие устойчивость модели при выдвинутых ограничениях на параметры.
С помощью математической модели противоборств «Защитник информационных ресурсов – нарушитель» был построен пробный прогноз в потребности специалистов информационной безопасности на рынке труда для одного из регионов страны до 2017 года. Примем начальную численность нарушителей равную 2500 человек (25*100), а численность защитников равную 1300 человек (13*100). За начало отсчета построения прогноза примем дату 1.01.2010, а шаг по времени будет составлять один квартал (3 месяца), тогда для получения прогноза до 2017 года зададим следующий интервал модельного времени [0;24]. Для построения прогноза были заданы исходные параметры модели, отображенные в таблице 1.
Таблица 1 – Исходные параметры модели
|
Параметр |
Значение |
Параметр |
Значение |
Параметр |
Значение |
|
|
0.7 |
|
0.65 при 0.52 при |
b |
0.3 |
|
|
23 тыс. руб./квартал |
R |
0.02 при 0.29 при |
i |
0.8 |
|
P |
9 тыс. руб./квартал |
|
0.5 |
|
0.02 |
|
|
0.2 |
Z |
12 тыс. руб./квартал |
|
|
|
c |
0.7 |
V |
0.6 при 0.21 при |
|
|
Пробный прогноз строился на базе системы математического моделирования AnyLogic. Построим траекторию системы (4) на основе входных параметров, перечисленных выше, отображенную на рисунке 2.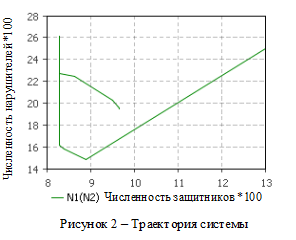
Рассмотрим динамику численностей нарушителей и защитников во времени до 2017 года, отображенную на рисунке 3, из которой видно, когда в модельный момент времени равный 7 (3 квартал 2011 г.) снижается качество подготовки защитников (параметр 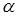 ) наблюдается рост численности нарушителей, что в свою очередь влечет к увеличению числа компьютерных преступлений.
) наблюдается рост численности нарушителей, что в свою очередь влечет к увеличению числа компьютерных преступлений.
В модельный момент времени равный 14 (2 квартал 2013 г.) происходит усиление строгости законодательства за совершение компьютерных преступлений (увеличение параметра R), такое изменение параметра повлияло на численность нарушителей, что означает отток нарушителей в другие сферы жизнедеятельности (становление на путь исправления), а значит это мероприятие является действенным для исследуемого региона.
В модельный момент времени равный 18 (2 квартал 2014 г.) происходит снижение уровня полезности защитников, что влечет к увеличению их численности для поддержания баланса сил исследуемого противоборства, но в тоже время наблюдается и уменьшение численности нарушителей.
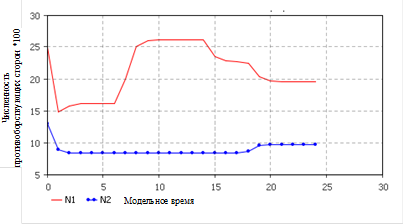
Рисунок 3 – Динамика численностей нарушителей и защитников
Как видно из рисунка 3 к концу 2017 года получаем следующий баланс сил на фронте противоборства: численность нарушителей будет составлять 19,49*100 = 1949 человек, а для сдерживания атак нарушителей необходимо подготовить 9,67*100 = 967 защитников информации.
Заключение
В результате исследований не было обнаружено разработанных методов, позволяющих прогнозировать потребность региона в специалистах в области информационной безопасности. В качестве решения данного вопроса была предложена математическая модель, использование которой поможет определить необходимое количество специалистов в области информационной безопасности, следовательно, позволит корректировать численность обучающихся студентов в высших учебных заведениях. Прогнозирование потребности в специалистах поможет сократить количество компьютерных преступлений, а также позволит частично снять проблему невостребованности на рынке труда в случае излишнего выпуска подготовленных студентов, которые теоретически могут пополнить ряды нарушителей.
Литература:
1. Манойло А. В., Петренко А. И., Фролов Д. Б., 2003 г.: Государственная информационная политика в условиях информационно-психологической войны, монография. — М.: Горячая линия ‑ Телеком, 541 с.: ил.
2. В.В. Смирнов, С.В. Николаев, С.В. Киниченко Технология имитационного моделирования процессов информационного противоборства. – Мехатроника, автоматизация, управление, 2007г.
3. A.M. Цыбулин Многоагентная модель для исследования противоборства службы безопасности и ассоциации злоумышленников. – Обозрение прикладной и промышленной математики, 2008г.
4. А.И. Буравлев, С.В. Гордеев Модель динамики противоборства неоднородных группировок сил. – Вооружение и экономика, 2009г.
5. В.И. Выпасняк, Д.Б. Калиновский, О.В. Тиханычев Моделирование вооруженного противоборства: перспективы развития. – Военная мысль, 2009г.
6. А.И. Буравлев Агрегированная модель противоборства боевых систем. – Вооружение и экономика, 2009г.
7. Д.А. Губанов, А.Г. Чхартишвили Об одной модели информационного противоборства в социальной сети. – Системы управления и информационные технологии, 2009г.
8. Почепцов Г. Г. Информационные войны. М.: «Рефл-Бук», К.: «Ваклер» — 2000. — 576 с.
9. Вольтерра В. Математическая теория борьбы за существование / В. Вольтерра; под ред. Ю.М. Свирежнева. М.: Наука, 1976. 286 с.
10. Формирование здорового образа жизни и профилактика социально значимых заболеваний: Учебно-методическое пособие/ Н.В.Лядова и др. – Пермь: ПОИПКРО, 2002. - 274 с.
11. Статистические методы анализа ускорения социально-экономического развития: Сб.науч.трудов./Самара.–1989. – 172 с.
12. Патронов К.С. Нравственное здоровье общества: количественная оценка // Омский научный вестник. – 2001. – вып.17. – С. 60–61.