Введение понятия нечеткого интеграла связано со стремлением к разработке в нечеткой математике аналогов, используемых в статистике и теории вероятностей понятий среднего и математического ожидания. Поскольку указанные понятия базируются на свойстве аддитивности вероятностной меры, а нечеткие меры более широкий класс мер, разработка указанных аналогов привела к построению принципиально новой математической конструкции [2].
Нечеткий интеграл от функции h : X → [0, 1] на множестве A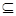 X по нечеткой мере g определяется как
X по нечеткой мере g определяется как
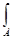 h(x)
h(x)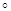 g =
g = 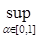 (α
(α g ( A ∩ Hα)), (1)
g ( A ∩ Hα)), (1)
где Hα={x | h(x)≥α}.
Нечеткий интеграл принято также называть нечетким ожиданием или FEV (fuzzy expected value).
Нечеткий интеграл от функции h : X → [0,1] на нечетком множестве A={x, μA(x)} по нечеткой мере g определяется как [3]
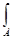 h(x)
h(x) g =
g =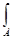 (μ A (x)
(μ A (x)  h( x))
h( x)) g (2)
g (2)
Отметим основные свойства нечетких интегралов.
Пусть a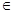 [0,1], (E, F
[0,1], (E, F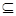 X ) и h: X → [0,1].
X ) и h: X → [0,1].
1. 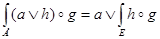 .
.
2. 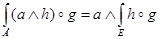 .
.
3. 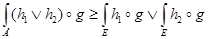 .
.
4. 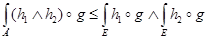 .
.
5. 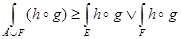 .
.
6. 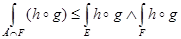 .
.
Можно показать, что понятие нечеткого интеграла сходно с понятием интеграла Лебега. Для этого рассмотрим разбиение множества X на непересекающиеся подмножества 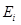 (рис.1):
(рис.1): ,
,  , i ≠ j, i=1,2,…,n.
, i ≠ j, i=1,2,…,n.
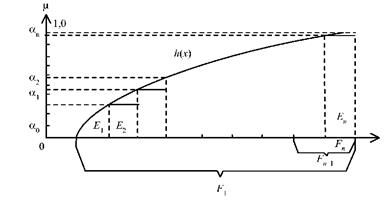
Рис. 1. Построение ступенчатой функции
Пусть 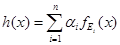 - ступенчатая возрастающая функция (h:X → [0,1]), где
- ступенчатая возрастающая функция (h:X → [0,1]), где
αi 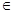 [0,1], Ei
[0,1], Ei 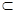 X , fEi - характеристическая функция обычного множества Ei, т. е. fEi (x) = 1, если x
X , fEi - характеристическая функция обычного множества Ei, т. е. fEi (x) = 1, если x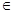 Ei, fEi (x) = 0, x ∉ Ei. Пусть l есть мера Лебега. Интеграл Лебега от функции h по множеству A определяется как
Ei, fEi (x) = 0, x ∉ Ei. Пусть l есть мера Лебега. Интеграл Лебега от функции h по множеству A определяется как
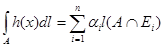 , (3)
, (3)
где i = {1, 2, 3 .... n}; α1 ≤ α2 ≤ α3 ≤ ... αn.
Введем множества Fi = 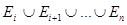 , i=1,2,…, n. Тогда h(x) может быть представлена в виде
, i=1,2,…, n. Тогда h(x) может быть представлена в виде 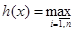
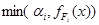 . В этом случае нечеткий интеграл по аналогии с интегралом Лебега может быть определен в виде:
. В этом случае нечеткий интеграл по аналогии с интегралом Лебега может быть определен в виде:
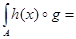
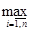
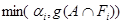 . (4)
. (4)
Сопоставляя (3) и (4), можно обнаружить сходство между данными интегралами: операции сложения и умножения для интеграла (3) заменены операциями max и min соответственно для (4) [1].
Оба интеграла – лебегов и нечеткий – можно сравнить, используя вероятностную меру. Если (X, B, Р) – вероятностное пространство, а h: X → [0,1] есть B-измеримая функция, то имеем, что
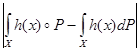
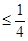 . (5)
. (5)
Сравнительно легко осуществлять расчет нечеткого интеграла в случае конечного множества X и соответственно конечного числа α, для которых требуется определить g(Hα). Для этого необходимо воспользоваться следующим утверждением.
Если функция h(x) принимает n+1 значение αi, то соответственно множество значений g(Hαi), отличных от 0 и 1, состоит из n элементов. В последовательности из 2n+1 элементов, составленной из элементов {αi} и {g(Hαi)}, расположенных в порядке возрастания, значение срединного n+1 элемента равно значению FEV(h).
На рис. 2 приведен пример графической интерпретации нахождения значения нечеткого интеграла для X = R [2]:
FEV(h)=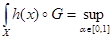
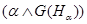 , где Hα={x | h(x)≥α}.
, где Hα={x | h(x)≥α}.
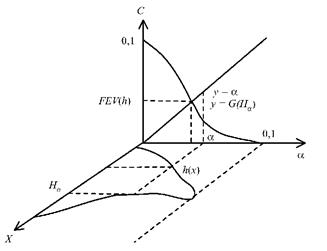
Рис. 2. Графическая интерпретация нечеткого интеграла
Для описания различных видов неопределенности в теории нечетких мер используется общее понятие "степень нечеткости". В общем случае оно включает в себя "степень важности", "степень уверенности" и как отдельный случай - "степень принадлежности" в теории нечетких множеств. Нечеткая мера, таким образом, может интерпретироваться различными способами в зависимости от конкретного применения.
Определение нечеткого множества, фиксирующего степень принадлежности элемента х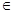 Х подмножеству А
Х подмножеству А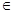 F(X), где F(Х) - множество всех нечетких подмножеств Х, может быть представлено с использованием нечеткого интеграла следующим образом [3].
F(X), где F(Х) - множество всех нечетких подмножеств Х, может быть представлено с использованием нечеткого интеграла следующим образом [3].
Пусть необходимо оценить степень принадлежности некоторого элемента 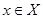 множеству
множеству 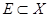 . Очевидно, что для пустого множества эта степень принадлежности равна 0, а для
. Очевидно, что для пустого множества эта степень принадлежности равна 0, а для 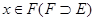 равна 1, т.е. степень принадлежности для
равна 1, т.е. степень принадлежности для 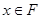 будет больше, чем для
будет больше, чем для 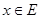 , если
, если 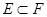 . Если степень принадлежности
. Если степень принадлежности 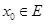 равна g(x0,E), а вместе E задано нечеткое подмножество
равна g(x0,E), а вместе E задано нечеткое подмножество 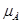 , то
, то 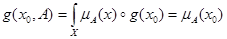 .
.
Это говорит о том, что степень нечеткости суждения “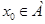 ” равна степени принадлежности
” равна степени принадлежности 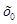 нечеткому подмножеству
нечеткому подмножеству 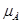 . Таким образом, понятие степени нечеткости в теории нечетких мер включает в себя понятие степени принадлежности теории нечетких множеств.
. Таким образом, понятие степени нечеткости в теории нечетких мер включает в себя понятие степени принадлежности теории нечетких множеств.
Для непрерывного пространства X=R вычисление нечеткого интеграла может быть упрощено и сведено к нахождению значения на монограмме (или таблице).
Пусть выполняется условие:
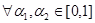
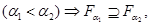 {x|h(x)≥αi}=Fαi.
{x|h(x)≥αi}=Fαi.
В этом случае справедливо следующее. Если f(x) – плотность нечеткой меры, значение нечеткого интеграла от h(x) по нечеткой мере равно значению 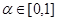 , для которого справедливо:
, для которого справедливо:
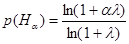 ,
, 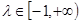 , (6)
, (6)
где
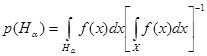 .
.
Правая часть (6) зависит только от значений α и λ и может быть получена заранее в числовом виде в форме таблицы или графика. Левая часть (6) представляет собой отношение области, определяемой уровневым множеством Hα, ко всей области определения функции плотности нечеткой меры f(x).
Использование (6), таким образом, может облегчить организацию вычисления нечеткого интеграла [1].
В качестве примеров рассмотрим вычисления нечеткого интеграла для конечных множеств в случаях gλ- и gv-мep.
Пусть задано пятиэлементное множество X={хi}, i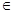 {1, 2, 3, 4, 5}. Каждому элементу хi
{1, 2, 3, 4, 5}. Каждому элементу хi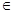 X соответствуют значения нечетких плотностей gi из табл.1.
X соответствуют значения нечетких плотностей gi из табл.1.
Таблица 1
|
i |
1 |
2 |
3 |
4 |
5 |
|
gi |
0,170 |
0,257 |
0,216 |
0,212 |
0,061 |
|
h(хi) |
0,5 |
0,7 |
0,1 |
0,2 |
0,3 |
Согласно условию нормировки для gi-меры получаем λ=0,25. Значение нечеткого интеграла 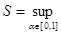
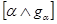 , где
, где 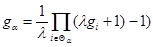 , Θα={i|h(xi)≥α},
, Θα={i|h(xi)≥α},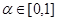 , принимает значение S=0,4379.
, принимает значение S=0,4379.
Для gv-мepы из условия нормировки можно получить
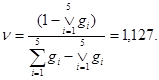
При этом значение нечеткого интеграла для gv -меры S = 0,448 [2].
Литература
Бочарников В.П. Fuzzy-технология: Математические основы. Практика моделирования в экономике. Санкт-Петер6ург: «Наука» РАН, 2001.- 328 с.
Павлов А.Н., Соколов Б.В. Принятие решений в условиях нечеткой информации. ГУАП- СПб., 2006 - 72 с.
Яхъяева Г.Э. Нечеткие множества и нейронные сети.– М.: Бином. Лаборатория знаний, 2008.- 320 с.







