Проблема обеспечения высокопрочными трубами для строительства и эксплуатации мощностей по добыче и транспортировке нефти и газа является одной из первоочередных государственных задач. Решение ее начинается с формулировки требований к качеству труб, связанных с повышением надежности и долговечности трубопроводного транспорта.
Одним из путей решения этой проблемы является использование в нефтегазовой отрасли труб из различных материалов, в том числе полимер содержащих [1].
Как известно, магистральные, технологические и промысловые газонефтепроводы представляют собой сложные инженерные конструкции, проложенные во многих регионах России и ряда республик СНГ и эксплуатируемые в разнообразнейших природно-климатических условиях. Следует отметить, что подземная, наземная и подводные прокладки трубопроводов, подводные переходы, различные электрохимзащиты от коррозии, особенности технологии строительства и конструктивных решений создают широкий спектр параметров прочности, устойчивости различных участков трубопроводов. В связи с тем, что в настоящее время при строительстве магистральных трубопроводов широко применяются трубы, изготовленные из различных естественных и искусственных (композитных) материалов при сложных климатических условиях, от проектировщика и расчетчика требуется максимально правильно оценить свойства материала трубы и реального грунта [2].
Целью данный работы является разработка математической модели, численного алгоритма и компьютерной программы для решения задачи о нелинейных колебаниях вязкоупругих тонкостенных трубопроводов большого диаметра на базе теории оболочек [3, 4].
Рассмотрим поведение тонкой круговой вязкоупругой цилиндрической оболочки, внутри которой с постоянной скоростью движется идеальная жидкость. Скорость жидкости равна U и имеет направление, совпадающее с направлением оси Ox.
Уравнения движения оболочки, полученные в рамках классических теории оболочек, с учетом наличия вязкоупругого основания, имеют вид [1, 5]:
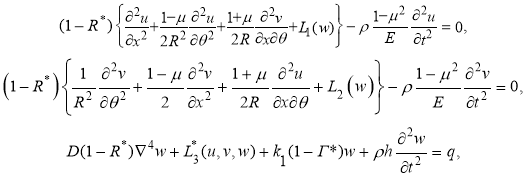 (1)
(1)
где D — цилиндрическая жесткость трубы, ![]() — коэффициент Пуассона материала трубы,
— коэффициент Пуассона материала трубы, ![]() — модуль упругости материала трубы,
— модуль упругости материала трубы, ![]() - его плотность;
- его плотность; ![]() — коэффициент основания Винклера, R − радиус кривизны срединной поверхности;
— коэффициент основания Винклера, R − радиус кривизны срединной поверхности; ![]() — толщина стенки трубы;
— толщина стенки трубы; ![]() – интегральный оператор вида:
– интегральный оператор вида: ![]() ;
; ![]() — ядро релаксации; операторы
— ядро релаксации; операторы ![]() ,
, ![]() ,
, ![]() будут такими:
будут такими:
![]()
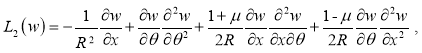
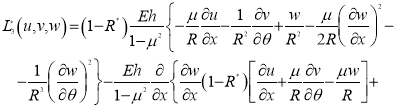
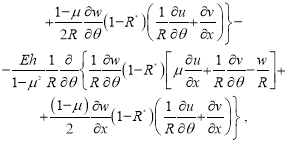
![]() давление жидкости на стенку трубопровода:
давление жидкости на стенку трубопровода:
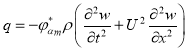 ,
,
где ![]() - присоединенная масса жидкости; m — число волн,
- присоединенная масса жидкости; m — число волн,![]() образующихся по окружности,
образующихся по окружности, ![]() — волновой число или постоянной распространения фазы.
— волновой число или постоянной распространения фазы.
Полученные нелинейные ИДУ в частных производных с помощью метода Бубнова-Галеркина при рассмотренных граничных условиях сводятся к решению систем нелинейных обыкновенных ИДУ с постоянными или переменными коэффициентами относительно функции времени. Для исследования колебательных процессов трубопровода предлагается численный алгоритм решение нелинейных интегро-дифференциальных уравнений с сингулярными ядрами. На основе разработанного вычислительного алгоритма создан комплекс прикладных программ. Численно исследовано влияние сингулярности в ядрах наследственности на колебания конструкций, обладающих вязкоупругими свойствами.
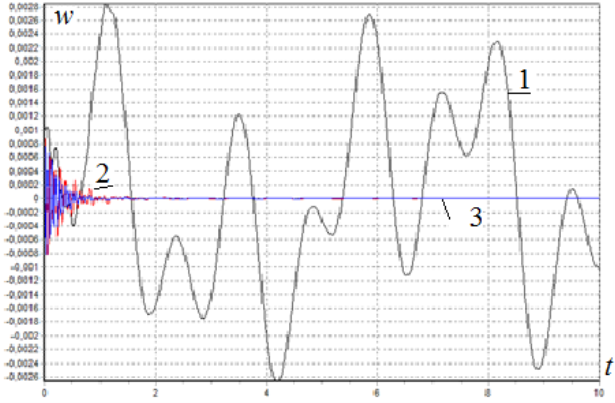
Рис. 1. Влияние параметра ![]() на амплитуда колебаний трубопровода: А=0,1;
на амплитуда колебаний трубопровода: А=0,1; ![]() =0,0 (1); 0,05(2); 0,1(3)
=0,0 (1); 0,05(2); 0,1(3)
Исследовано влияние вязкоупругих свойств основания грунта на колебательный процесс трубопровода (рис. 1). Решение упругой и вязкоупругой задачи в начальный период времени мало отличается друг от друга. С течением времени вязкоупругие свойства оказывает существенное влияние, что приводит к заметному отличию решений. Заметим также, что с увеличением параметра вязкости оснований грунта амплитуда колебаний быстро затухает.
На рис. 2 показаны кривые изменения w по времени при разных значениях ![]() . Кривые 1–3 соответствуют значениям
. Кривые 1–3 соответствуют значениям ![]() =0;
=0; ![]() =0,5 и
=0,5 и ![]() = 1. Как видно из графиков, с ростом параметра
= 1. Как видно из графиков, с ростом параметра ![]() происходит биение.
происходит биение.
Из приведенного следует, что с увеличением коэффициента основания
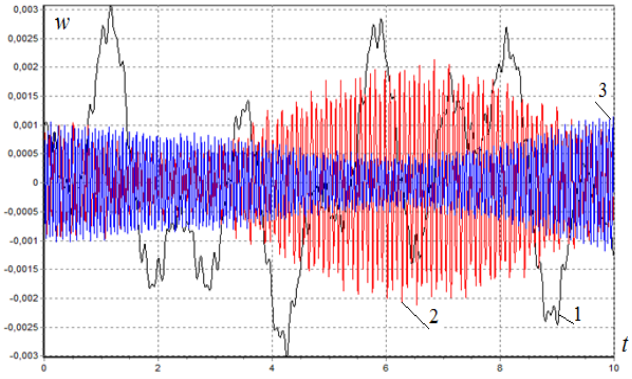
Рис. 2. Зависимость амплитуд прогиба w от безразмерной времени t при ![]() =0 (1); 0,5(2); 1(3)
=0 (1); 0,5(2); 1(3)
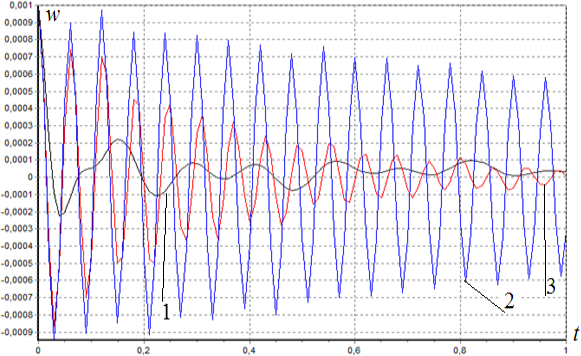
Рис. 3. Влияние сингулярного параметра ![]() на амплитуду колебаний трубопровода: А=0;
на амплитуду колебаний трубопровода: А=0; ![]() ,
, ![]()
![]() 0,1 (1); 0,3(2); 0,6(3)
0,1 (1); 0,3(2); 0,6(3)
На рис. 3 показан характер движения трубопровода при различных реологических параметрах основания ![]() . При
. При ![]() амплитуды колебаний трубопровода с течением времени уменьшаются. Рост реологического параметра
амплитуды колебаний трубопровода с течением времени уменьшаются. Рост реологического параметра ![]() =0.6 приводит к увеличению частоты и амплитуды колебаний трубопровода.
=0.6 приводит к увеличению частоты и амплитуды колебаний трубопровода.
Необходимо отметить, что алгоритм предлагаемого метода позволяет детально исследовать влияние геометрических нелинейностей и вязкоупругих свойств материала конструкций на колебательные процессы вязкоупругих трубопроводов, в частности, при исследовании свободных колебаний трубопроводов на базе теории идеально-упругих оболочек. Полученные результаты численного моделирования могут быть использованы в предприятиях нефтегазовой отрасли, а также проектными организациями.
Литература:
- Якубовская С. В., Сильницкая Н. Ю., Иванова Е. Ю. Явление ползучести и релаксации армированных полиэтиленовых трубопроводов // Фундаментальные исследования. 2015. № 2. — С.1676–1680.
- Гаджиев В.Дж., Расулова С. Р., Джафаров Х. Г. Свободное колебание прямоугольного участка неоднородного трубопровода, лежащего на двух константном основании // Нефтегазовое дело. 2015, Т. 13. № 4. — С. 137–141.
- Вольмир А. С. Оболочки в потоке жидкости и газа. Задачи гидроупругости. — М.: Наука. 1979. — 320 с.
- Григолюк Э. И., Мамай В. И. Нелинейное деформирование тонкостенных конструкций. — М.: Наука. Физматлит, 1997. — 272 с.
- Худаяров Б. А., Тураев Ф. Ж. Моделирование динамических процессов трубопроводов с протекающей жидкостью // Сборник трудов IV- международная школа конференция молодых ученых «Нелинейная динамика машин» 18–21 апрель 2017 г. М.: ИМАШ РАН, 2017. — С. 449–454.







