Данная работа посвящена исследованию задачи нахождения k-error линейной сложности бинарной последовательности. Написаны программы нахождения точного решения k-error линейной сложности для частных случаев.
Ключевые слова: бинарная последовательность, линейная сложность, k-error линейная сложность, алгоритм Берлекэмпа — Мэсси, алгоритм Стэмпа и Мартина.
Известно, что такое свойство последовательности, как линейная сложность, значимо в определении криптографически сильных последовательностей. Введем основные определения.
Дана бесконечная последовательность 𝑠 = ![]() ,
, ![]() , ... (либо конечная последовательность 𝑠 =
, ... (либо конечная последовательность 𝑠 = ![]() ,
, ![]() , . . . ,
, . . . ,![]() ) с элементами из поля 𝐾.
) с элементами из поля 𝐾.
Определение 1. Говорят, что 𝑠 является линейной рекуррентной последовательностью порядка 𝐿 (𝐿 > 0), если для членов этой последовательности выполняется соотношение
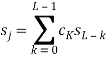
для любых 𝑗 = 𝐿, 𝐿 + 1, . . . (или для любых 𝑗 = 𝐿, 𝐿 + 1, . . . , 𝑡 – 1 соответственно), где ![]() , . . . ,
, . . . , ![]() ∈ {0, 1}.
∈ {0, 1}.
Это уравнение называют линейным рекуррентным отношением порядка 𝐿.
Определение 2. Минимальное 𝐿, такое что 𝑠 является линейной рекуррентной последовательностью порядка 𝐿, называется линейной сложностью последовательности 𝑠.
Cуществует эффективный метод нахождения линейной сложности конечной или периодической последовательности, описанный в источнике [1], известный как алгоритм Берлекэмпа — Мэсси (Berlekamp — Massey Algorithm, BMA).
Пример. Рассмотрим 20-периодичную последовательность 𝑠 с циклом
![]() = 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0.
= 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0.
Ее линейная сложность, посчитанная при помощи алгоритма Берлекэмпа-Мэсси, равна 19.
Пусть дана бесконечная двоичная последовательность 𝑠 = ![]() ,
, ![]() , ... Через
, ... Через ![]() обозначим линейную сложность подпоследовательности
обозначим линейную сложность подпоследовательности ![]() =
= ![]() ,
, ![]() , . . . ,
, . . . ,![]() , 𝑁 > 0.
, 𝑁 > 0.
Последовательность ![]() ,
, ![]() , ... называется профилем линейной сложности последовательности 𝑠. В случае конечной последовательности профиль линейной сложности состоит из
, ... называется профилем линейной сложности последовательности 𝑠. В случае конечной последовательности профиль линейной сложности состоит из ![]() ,
, ![]() , . . . ,
, . . . ,![]() .
.
Рассмотрим периодическую последовательность ![]() , введенную ранее в примере. Ее профиль линейной сложности, имеющий вид: 1, 1, 1, 3, 3, 3, 3, 5, 5, 5, 6, 6, 6, 8, 8, 8, 9, 9, 10, 10,11, 11, 11, 11, 14, 14, 14, 14, 15, 15, 15, 17, 17, 17, 18, 18, 19, 19, 19, 19, ... , изображен на Рис. 1.
, введенную ранее в примере. Ее профиль линейной сложности, имеющий вид: 1, 1, 1, 3, 3, 3, 3, 5, 5, 5, 6, 6, 6, 8, 8, 8, 9, 9, 10, 10,11, 11, 11, 11, 14, 14, 14, 14, 15, 15, 15, 17, 17, 17, 18, 18, 19, 19, 19, 19, ... , изображен на Рис. 1.
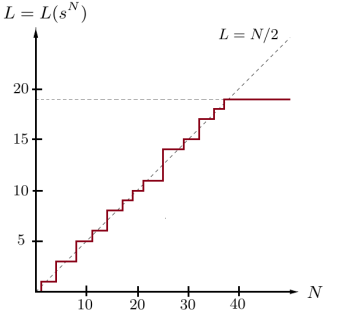
Рис. 1.
Понятие линейной сложности было обобщено до 𝑘-error линейной сложности — минимальной линейной сложности последовательности, в которой по крайней мере 𝑘 элементов были изменены. Эта концепция была впервые изложена Ding, Xiao, Shan [2], которые назвали ее весовой сложностью, и получила название 𝑘-error линейной сложности в работе авторов Stamp и Martin [3]. Это свойство последовательности является важным критерием безопасности потоковых шифров и применяется к проблеме идентификации криптостойких псевдослучайных последовательностей.
Пусть 𝑠 =
![]() (
(![]() , . . . ,
, . . . , ![]() ) — вес Хэмминга последовательности
) — вес Хэмминга последовательности ![]() = (
= (![]() , . . . ,
, . . . , ![]() ).
).
Определение 3. Линейная сложность с k-кратной ошибкой (или k-error линейная сложность) бесконечной периодической последовательности 𝑠 определяется как
![]() (𝑠) =
(𝑠) = ![]() {𝐿(𝑠 + 𝑒) | 0
{𝐿(𝑠 + 𝑒) | 0 ![]()
![]() (
(![]() , . . . ,
, . . . , ![]() )
) ![]() 𝑘},
𝑘},
где 𝑒 — периодическая последовательность из поля 𝐾 с периодом 𝑁.
Последовательности 𝑒 называют вектором ошибок.
Определение 4. Последовательность ![]() (𝑠),
(𝑠), ![]() (𝑠),
(𝑠), ![]() (𝑠), . . . называется профилем 𝑘-error линейной сложности последовательности 𝑠.
(𝑠), . . . называется профилем 𝑘-error линейной сложности последовательности 𝑠.
Замечание 1. В этой работе в качестве поля 𝐾 будет использоваться поле Галуа 𝐺𝐹(2) с операцией сложения по модулю 2, то есть его элементами будут двоичные последовательности длины 𝑡. Тогда вес Хэмминга некоторой последовательности 𝑠, ![]() (𝑠), будет определяться как количество единиц в этой последовательности.
(𝑠), будет определяться как количество единиц в этой последовательности.
Не существует общего алгоритма для вычисления профиля 𝑘-error линейной сложности произвольной последовательности над произвольным конечным полем, кроме полного перебора.
Точный алгоритм для вычисления 𝑘-error линейной сложности бинарных последовательностей с периодом ![]() , 𝑚 > 1, был предложен авторами Stamp и Martin [3]. Этот эффективный алгоритм является расширением алгоритма Games и Chan [4], предназначенным для вычисления линейной сложности таких последовательностей.
, 𝑚 > 1, был предложен авторами Stamp и Martin [3]. Этот эффективный алгоритм является расширением алгоритма Games и Chan [4], предназначенным для вычисления линейной сложности таких последовательностей.
В качестве длины последовательности мы будем брать значения, равные степени 2. Такая локализация нужна для того, чтобы можно было вычислить точные значения 𝑘-error линейной сложности при помощи алгоритма Stamp и Martin. В дальнейшем тестирование будет проходить на бесконечных периодических последовательностях с данным полным периодом. Рассмотрим бинарные последовательности с периодом 𝑛 = ![]() = 32.
= 32.
Начиная с 𝑘=0, будем запускать алгоритм, увеличивая значение 𝑘, пока 𝑘-error линейная сложность не станет равна нулю. Таким образом, мы получим профиль 𝑘-error линейной сложности последовательности 𝑠. Мы применяем алгоритм Stamp и Martin для выборки из 10 последовательностей периода 32 с линейной сложностью 32 (таблица 1), результаты которого представлены в таблице 2. Видно, что выполняется основное свойство 𝑘-error линейной сложности: при увеличении 𝑘 линейная сложность последовательностей уменьшается.
Таблица 1
Тестовые последовательности
|
Последовательность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2
Профиль k-error линейной сложности бинарных последовательностей
|
|
Профиль k-error линейной сложности бинарных последовательностей |
|
|
32, 29, 29, 21, 21, 9, 9, 9, 9, 9, 9, 9, 9, 3, 3, 1, 1, 0 |
|
|
32, 29, 29, 20, 20, 13, 13, 10, 10, 5, 5, 4, 4, 0 |
|
|
32, 22, 22, 15, 15, 11, 11, 3, 3, 3, 3, 3, 2, 2, 0 |
|
|
32, 29, 29, 21, 21, 17, 17, 17, 17, 17, 17, 9, 9, 1, 1, 1, 1, 1, 1, 0 |
|
|
32, 26, 26, 23, 23, 17, 17, 17, 17, 17, 17, 9, 9, 3, 3, 1, 1, 0 |
|
|
32, 27, 27, 25, 25, 21, 21, 9, 9, 9, 9, 5, 5, 5, 5, 1, 1, 0 |
|
|
32, 25, 25, 25, 25, 21, 21, 17, 17, 7, 7, 5, 5, 2, 1, 1, 0 |
|
|
32, 25, 25, 25, 25, 25, 25, 9, 9, 7, 7, 5, 5, 0 |
|
|
32, 29, 25, 25, 25, 19, 19, 17, 17, 6, 6, 3, 3, 0 |
|
|
32, 29, 29, 25, 25, 17, 17, 17, 17, 17, 17, 5, 5, 2, 2, 0 |
Таким образом, при помощи реализованных точных алгоритмов удалось вычислить линейную сложность некоторых последовательностей, а также их k-error линейную сложность. При нахождении профиля k-error линейной сложности видно, что соблюдается основное свойство данной характеристики, о котором говорилось ранее.
Код, при помощи которого были получены приведенные выше результаты, доступен по ссылке https://github.com/cafecco/k-error-linear-complexity.
Литература:
- Massey J.L., Serconek S. Linear Complexity of Periodic Sequences // Lecture Notes in Computer Science. New York: Springer, 1996. V. 1109, P. 358–371.
- Ding C., Xiao C., Shan W. The Stability Theory of Stream Ciphers // Lecture Notes in Computer Science. Heidelberg: Springer-Verlag. 1992.
- Stamp M., Martin C.F. An Algorithm for the 𝑘-Error Linear Complexity of Binary Sequences with Period 2𝑛 // IEEE Transactions on Information Theory. 1993. V. 39, № 4, P. 1398–1401.
- Games R.A., Chan A.H. A Fast Algorithm for Determining the Complexity of a Binary Sequence with Period 2𝑛 // IEEE Transactions on Information Theory. 1983. V. 29, № 1, P. 144–146.







