Рассмотрим уравнение
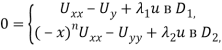 (1)
(1)
где ![]() λ1
λ1![]() λ2
λ2![]() –действительные постоянные;
–действительные постоянные; ![]() —прямоугольник, ограниченный отрезками
—прямоугольник, ограниченный отрезками ![]() прямых
прямых ![]() соответственно;
соответственно; ![]() - треугольник, ограниченный характеристиками
- треугольник, ограниченный характеристиками
![]()
![]()
уравнения (1) при ![]() .
.
Введем обозначения:
![]()
![]()
![]()
![]()
![]()
![]()
Здесь ![]() и
и ![]() — известные операторы, введенные в [1].
— известные операторы, введенные в [1].
Задача ![]() Требуется определить функцию и
Требуется определить функцию и ![]() , обладающую следующими свойствами:
, обладающую следующими свойствами:
1) ![]() регулярное в области
регулярное в области ![]() и обобщенное класса
и обобщенное класса ![]() [2] в области D2 решение уравнения (1);
[2] в области D2 решение уравнения (1);
2) ![]() удовлетворяет граничным условиям
удовлетворяет граничным условиям
![]() (2)
(2)
![]() (3R)
(3R)
3) на отрезке ![]() выполняются условия склеивания
выполняются условия склеивания
![]() (5R)
(5R)
Где ![]() — заданные функции, причем
— заданные функции, причем ![]()
![]()
![]()
![]()
![]() (y) удовлетворяет условию Гельдера с показателем
(y) удовлетворяет условию Гельдера с показателем ![]() ;
;
![]() ,
, ![]() Здесь и далее
Здесь и далее ![]() , 1. Без ограничения общности положим
, 1. Без ограничения общности положим ![]() и
и ![]() .
.
Отметим, что краевые задачи с нелокальными условиями склеивания для параболо-гиперболических уравнений известны в физике и изучены в работе [3].
Функциональное соотношение между ![]() и
и ![]() , принесенное на отрезок
, принесенное на отрезок ![]() из параболической части смешанной области D имеет вид [4]
из параболической части смешанной области D имеет вид [4]
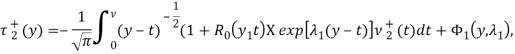
а из гиперболической части в задаче
![]() (7)
(7)
где k0![]() Ф1
Ф1![]() 1
1![]() Ф2
Ф2![]() — известные функции.
— известные функции.
Исключив ![]() (у) из (6) и (7), с учетом условий склеивания (4о) и (5о) получим У
(у) из (6) и (7), с учетом условий склеивания (4о) и (5о) получим У
![]() (8)
(8)
где
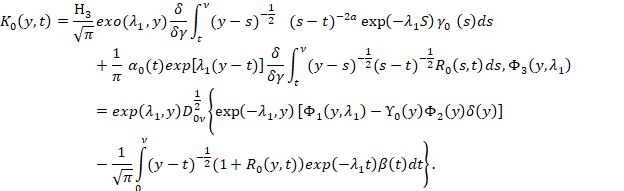
Анализ уравнения (8) показывает, что ядро ![]() является квадратично суммируемым в [0,1] x [0,1],
является квадратично суммируемым в [0,1] x [0,1], ![]() Следовательно, существует единственное непрерывное решение интегрального уравнения Вольтерра второго рода (8) [5].
Следовательно, существует единственное непрерывное решение интегрального уравнения Вольтерра второго рода (8) [5].
При исследовании задачи ![]() учтем, что в определении обобщенного класса решений
учтем, что в определении обобщенного класса решений ![]() уравнения (1) в области
уравнения (1) в области ![]() необходимо взять
необходимо взять
![]()
![]()
где
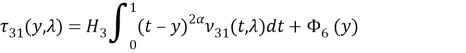 (9)
(9)
где
![]()
Аналогично задаче ![]() решение задачи
решение задачи ![]() \ сведем к доказательству существования решения интегрального уравнения Фредгольма с квадратично интегрируемым ядром и непрерывной правой частью
\ сведем к доказательству существования решения интегрального уравнения Фредгольма с квадратично интегрируемым ядром и непрерывной правой частью
![]() (10)
(10)
где
![]()
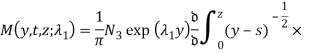
![]()
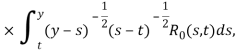
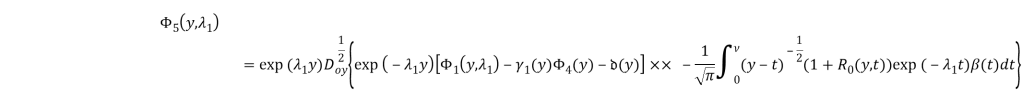
Разрешимость последнего следует из [4] и теоремы.
Теорема единственности. Если выполнены условия
![]()
то задача ![]() не может иметь более одного решения.
не может иметь более одного решения.
Литература:
- Салахитдинов М. С., Уринов А. К. Дифференциальные уравнения и их приложения к механике. Ташкент: Фан, 1986. С. 3–14.
- Эргашев Т. Г.// Докл. АН УзССР. 1989. № 12. С. 3- 5.
- Капустин Н. Ю.//Докл. АН СССР. 1989. Т. 305. № 1. С. 31–33.
- Бабич В. М., Капилевич М. Б. и др. Линейные уравнения математической физики. М.: Наука, 1964. 368 с.
- Михлин С. Г. Лекции по линейным интегральным уравнениям. М.: Физматгиз, 1959, 224, с.







