Рассмотрим уравнение
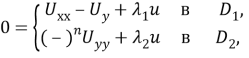 (1)
(1)
где ![]()
![]() — действительные постоянные; D1— прямоугольник, ограниченный отрезками АВ, ВВ1, В1А1, А1А прямых
— действительные постоянные; D1— прямоугольник, ограниченный отрезками АВ, ВВ1, В1А1, А1А прямых![]()
![]() соответственно;
соответственно; ![]() — область, ограниченная отрезком
— область, ограниченная отрезком ![]() оси Оy и двумя характеристиками
оси Оy и двумя характеристиками
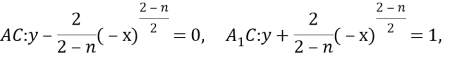
![]() уравнения (1) при
уравнения (1) при ![]() Примем обозначения
Примем обозначения
![]()
![]()
![]()
Задача T2. Требуется определить функцию u (х, у), обладающую следующими свойствами: 1) ![]() ; 2)
; 2)![]() — регулярное решение уравнения (1) в области
— регулярное решение уравнения (1) в области ![]() ; 3)
; 3) ![]() — обобщенное решение уравнения (1) класса
— обобщенное решение уравнения (1) класса ![]() в области D2; 4)
в области D2; 4) ![]() удовлетворяет граничным условиям
удовлетворяет граничным условиям
![]() (3)
(3)
5) на отрезке АА1 выполняется условие склеивания вида
![]() yϵI (4)
yϵI (4)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (у) — за энные функции, причем
(у) — за энные функции, причем ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() (у)
(у) ![]() ,
, ![]()
![]() ,
, 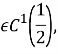 ,
, ![]() при
при ![]() ,
, ![]()
![]()
может обращаться в бесконечность порядка не выше ![]() при
при ![]() 0.
0.
Следует отметить, что задача ![]() изучалась для параболо-гипер- болических уравнений: для общего уравнения с одной линией вырождения первого рода [2]; для модельного уравнения с негладкой линией вырождения второго рода [3].
изучалась для параболо-гипер- болических уравнений: для общего уравнения с одной линией вырождения первого рода [2]; для модельного уравнения с негладкой линией вырождения второго рода [3].
При исследовании задачи ![]() важную роль играют функциональные соотношения между
важную роль играют функциональные соотношения между ![]() и
и ![]() , принесенные на отрезок
, принесенные на отрезок ![]() из параболической [2, 4] и гиперболической [1] частей смешанной области D
из параболической [2, 4] и гиперболической [1] частей смешанной области D
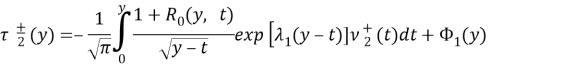 (5)
(5)
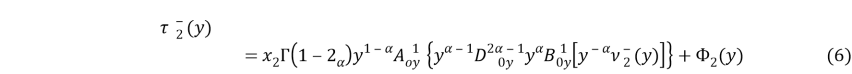 где
где ![]() -
-
известные операторы и функции, приве енные соответственно в работах |5] и [1, 2, 4].
Соотношение (6) приведем к виду
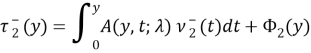 (7)
(7)
где
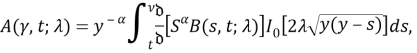
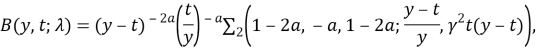
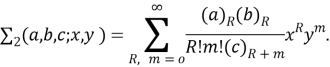
При получении соотношения (7) мы использовали вид операторов ![]() и тождество
и тождество
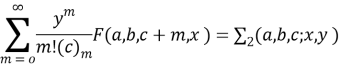
С учетом условия (4) и ![]() из (-5) и (7) будем иметь
из (-5) и (7) будем иметь
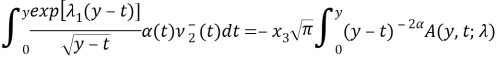
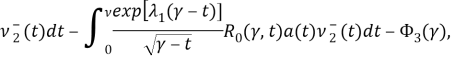
где
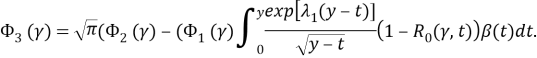
Обратив последнее как обобщенное интегральное уравнение Абеля, получим
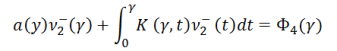 (8)
(8)
где
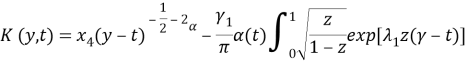
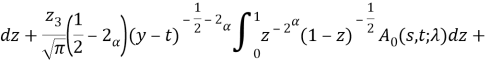
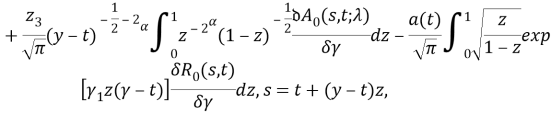
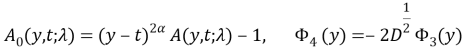
Исследуем гладкость ядра ![]() Очевидно, гладкость ядра
Очевидно, гладкость ядра ![]() определяется гладкостью первого слагаемого правой части. Следовательно, ядро
определяется гладкостью первого слагаемого правой части. Следовательно, ядро ![]() имеет слабую особенность. Исследование правой части (8) показывает, что
имеет слабую особенность. Исследование правой части (8) показывает, что ![]()
Таким образом, равенство (8) является интегральным уравнением Вольтерра второго рода. На основании этого заключаем, что существует единственное решение задачи ![]()
Замечание. В постановке задачи
Литература:
- Эргашев Т. Г.//Докл. АН УзССР. 1989. № 12. С. 3–5.
- Е леев В. А,//Дифференциальные уравнения. 1977. Т. 13. № 1. С, 53–56.
- Исамухамедов С.С, //Вырождающиеся дифференциальные уравнения и обратные задачи: Сб. ст. Ташкент: Фан, 1986. С. 98–113.
- Джураев Т. Д., Апаков Ю. П. // Йзв. АН УзССР. Сер. ф.-м. наук. 1986. № 3. С. 21–27.
- Салахитдинов М. С., Уринов А. К.., //Дифференциальные уравнения и их приложения к механике: Сб. ст. Ташкент, 1985. С.







