Математическая модель технологического процесса обогащения каолина



Кинетические кривые роста микроорганизмов, содержащиеся в субстратах, в закрытых системах имеют сложный характер. Выделяют несколько фаз в развитии культуры (рис.1).

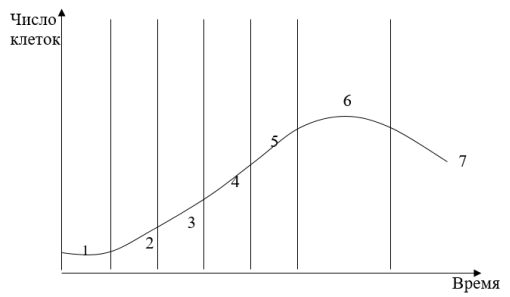
Рис. 1. Кривая роста популяции микроорганизмов

1. После введения инокулянта обычно наблюдают индукционный период (лаг-фазу) (1).
2. Индукционный период сменяется фазой экспоненциального роста (2), в течение которой быстро накапливаются биомасса и продукты разных реакций.
3. В фазу линейного роста (3), характеризующегося равномерным во времени линейным ростом культуры.
4. Фаза линейного роста может смениться весьма непродолжительным периодом, в течение которого скорость роста культуры снижается до нуля. Эта фаза замедления роста (4).
5. Стационарная фаза. При этом скорость прироста биомассы полностью компенсируется скоростью гибели и лизиса клеток (5).
6. Фаза отмирания культуры (6) сопровождаемая часто полным лизисом клеток.

Время генерации Th ferrooxidans можно рассчитать по формуле

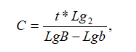(1)

где: — время генераций бактерий, — исходное число бактерий, — количество бактерий в конце опыта, — продолжительность опыта в часах. Коэффициент 2 принят нами потому, что прирост количества бактерий рассчитывается по ассимиляции здесь мы имеем дело с живыми клетками. При разработке метода учета этих бактерий, при их совместном присутствии мы попытались воспользоваться тем фактом, что имеющиеся у нас чистые культуры Th ferrooxidans и Th thiooxidans на среде Ваксмана с серой проявился полностью за 10 суток при исходном его содержании от 10 до 10 000 клеток в 1 мл то Th ferrooxidans только через две недели при исходном его содержании 10000 клеток в 1 мл. При исходном его содержании 10 и 100 клеток в 1 мл не был рост отмечен даже через 40 суток.

Величину суточного хемосинтеза рассчитывают по следующей формуле:

(2)

где:- где величина суточного хемосинтеза в мг углерода на 1л, -содержание углерода в воде, — общая радиоактивность воды в склянках, t — срок инкубации склянок в сутках.

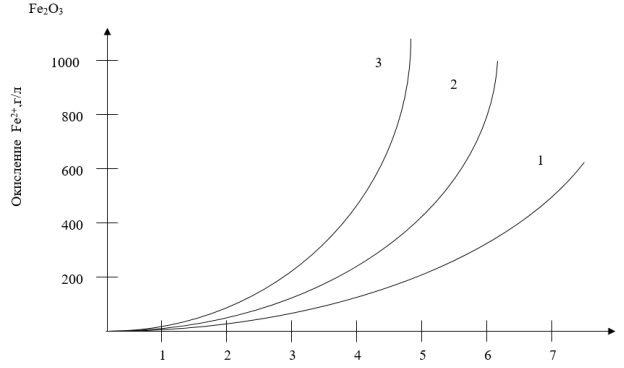
Влияние аэрации идобавок (фосфорнокислый) на скорость бактериального окисления в чанах: 1-без аэрации, 2-с аэрацией, 3-с аэрацией +

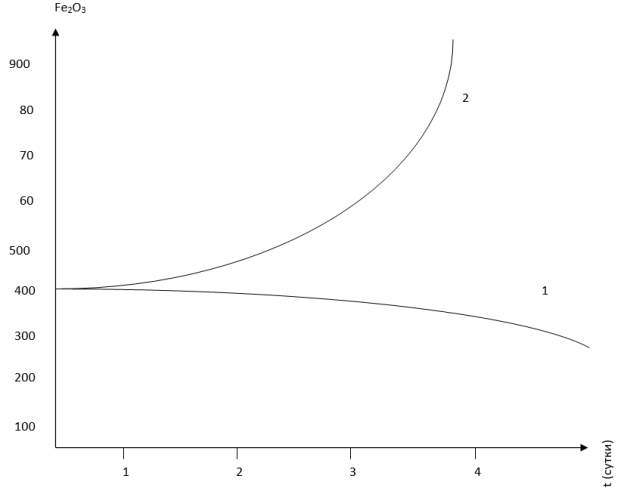
Рис.2. Влияние аэрации и добавок Th ferrooxidans на скорость регенерации 1-Fe²⁺,2-Fe³⁺

Расчеты показывают, что в случае непрерывного окисления при 31⁰ и рН 2,2 Тh ferroxidans может окислять Fe²⁺ со скоростью примерно в 500000 раз большей чем скорость химического окисления закисного железа. Th ferroxidans, как известно, был выделен как организм, способный окислять закисное железо в окисное в кислой среде. Этот процесс бактериального окисления двухвалентного железа идет настолько энергично, что был запатентован в США в 1958 году. Роль Th ferroxidans в окислении закисного железа в настоящее время хорошо изучена.

Результаты опытов, проведенных в различных условиях, показывают, что Th ferroxidans быстро окисляет закисное железо, тогда как химический процесс идет очень медленно. Скорость бактериального окисления закисного железа спонтанной микрофлорой была увеличена путем аэрирования растворов и добавления солей фосфора, что видно из данных. При дополнительной аэрации сжатым воздухом (2,8–3,0 м³/мин) и добавлением бактериальных затравок из чанов при температуре 20–31 градусов в условиях стационарного культивирования и при избытке кислорода, двуокиси углерода и других компонентов. Кинен установил, что Th ferroxidans способен окислять Fe²⁺ со скоростью в 200000 раз большей, чем этот процесс идет без бактерий. Таким образом, Th ferroxidans является весьма эффективным в окислении двухвалентного железа и может быть использован для регенерации выщелачивающих растворов.

При этом процесс использования субстрата бактериями можно представить в виде следующего уравнения:

(3)

где Sp — количество субстрата, потребленный на рост бактерий, г/л; - коэффициент, учитывающий часть расхода субстрата на рост единицы бактерий, г/г; — концентрация бактерий, г/л; x — удельная скорость роста бактерий, представляющая собой прирост клеточной массы, которая дает единицу активной биомассы в единицу времени, г^-1.

В процессе потребления субстрата бактериями образуются новые клетки. Данный процесс можно описать следующим уравнением:

(4)

Удельная скорость роста бактерии характеризует физиологические свойства. Железоокисляющая бактерия получает энергию для своего развития за счет окисления закисного железа, потребляет углеродов для своего развития за счет окисления закисного железа, потребляет углеродов для своего развития из карбонат-иона, растворенного в питательной среде. Бактерия нуждается также в других биогенных элементах, азоте, фосфоре, калии магнии. Она зависит от концентрации субстрата, наличия ингибиторов и активаторов в среде, температуры и рН среды. Оптимальная рН в каждом конкретном случае подбирается экспериментально. Для сульфидных минералов, выявлено, что наибольшая скорость их окисления в области рН 2,2–2,6 оптимального для развития бактерии Th ferroxidans.

Значение определяется с учетом концентрации субстрата

одного ингибитора, в ней не учитывается влияние таких показателей, как рН и Т, хотя эти параметры и оказывают значительное воздействие на физиологическое состояние клеток бактерий скорость их роста. Для расчета используем следующую форму:

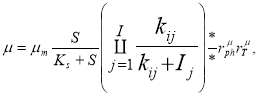(5)

гдe K_ij — константа, численно равная концентрации ингибитора, когда ; I_j- концентрация j-го ингибитора; - степень влияния рН на удельную скорость роста бактерий; - степень влияния Т на удельную скорость роста бактерий в зависимости от рН при постоянстве значений остальных параметров.

Расход субстрата на поддержание жизнедеятельности бактерий описывается уравнением

где Sж-количество субстрата, потребленного на поддержание жизнедеятельности концентрации клеток бактерий; S - константа пропорциональности, равная удельной скорости потребления субстрата на поддержание жизнедеятельности единицы концентрации клеток бактерий. Параметром (оптимизации) в этой задаче служила скорость окисления Fe.

Скорость окисления Fe выражается следующим уравнением

(6)

где t — время, час; S — концентрация, г/л; - максимум специфической скорости роста бактерий, час; y — сырая масса бактерий, образовавшаяся на 1 г окисленного железа, г/л; K — константа насыщения, г/л; X — концентрация бактерий, г/л.

При выборе культур микроорганизмов для биотехнологии важное значение имеет время генерации бактерий (время удвоения клеток) так как этот фактор определяет эффективность процесса в целом.

С учетом кинетических зависимостей составим уравнение описывающее процесс культивирования бактерий в непрерывном режиме:

(7)

С учетом функции степени принадлежности, заданных экспериментальными данными, которая аналитически выражается как

(8)

решаем уравнение (7).

Результаты решения уравнения (7) в частности для процесса обезжелезивания каолина приведена в графическом виде:

Литература:

1. Батунер Л. М., Позин М. Е. Математические методы в химической технике. М., Химия.
2. Исселдование процесса обогащения каолина в гидроциклоне. М.,1956.
3. Послешпатовое сырье Средней Азии для производства фарфора. Исматов А. А., Юнусов М. Ю., Максудов Д. И.
4. Каравайко Г. И. Микробиологические процессы выщелачивания металлов из руд. М., 1984.
5. Математическое моделирование микробиологических процессов. Пущина на Оке. 1973.
6. Булавин И. А. Машины и автоматические линии для производства тонкой керамики. М., Машиностроение, 1979.