Пограничный слой многокомпонентной жидкости



Рассмотрим обтекание плоской пластинки вязкой двухкомпонентной жидкостью, имеющей на бесконечности скорость . Задача решается на основе теории о взаимопроницаемом движении многокомпонентной сплошной среды, выдвинутой Х. А. Рахматулиным.

Введем систему координат с осью х, направленной вдоль обтекаемой стенки и с осью у, перпендикулярной к стенке.

В случае плоского установившегося движения двухкомпонентной жидкости имеем уравнение:

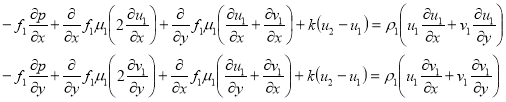
для первой компоненты;

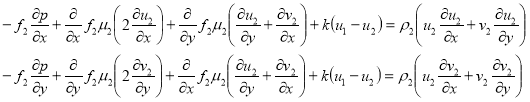
для второй компоненты:

Уравнение неразрывности:

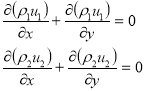
Кроме того , где составляющие скорости одной среда по осям прямоугольной системы координат; составляющие другой среды; - приведенные или средние плотности; - отношение средней плотности к истинной для одной и другой среды; т. е.

коэффициенты вязкости, р- давление, К- постоянной коэффициент, кт- сек²/м⁴; истинные плотности компонент.

Если изменением и в пределах пограничного слоя можно пренебречь, то уравнение неразрывности примет вид

Рассмотрим как раз этот случай.

Для вывода уравнения пограничного слоя будем пользоваться уравнением движения для первой компонента (для второй компоненты рассуждения аналогичны).

После наших предложений они запишутся в виде:

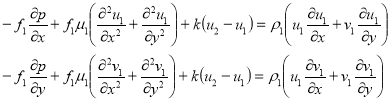
и уравнение неразрывности

Значения скорости изменяются от нуля на стенке до на границе пограничного слоя, толщину которого обозначим через .

Считая величиной малой, увидим, что в пограничном слое будет R порядка . Величины будут иметь порядок 1. Из уравнения неразрывности следует, что и производная порядка 1, а так как при то скорость будет порядка . Производные имеют тот же порядок , тогда как имеет порядок .

Поэтому в первом уравнении можно пренебречь производной по сравнению с и это уравнении производится к виду

где

Из этого видно, что член, зависящий от вязкости, того же порядка величины, что и квадратичные члены, зависящие от сил инерции.

Следовательно, (символ О означает, что сравниваемые величины одного порядка).

Второе уравнение приведется к следующему:

Полное изменение давления на протяжении пограничного слоя по нормали к пластинке будет, следовательно, порядка и им можно пренебречь. Таким образом, в пограничном слое можно считать давление постоянном вдоль нормали к пластинке и равным тому значению, которые оно имеет в основном потоке на внешней границе пограничного слоя.

После производных оценок запишем получившиеся уравнения:

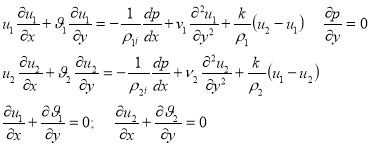
На пластинке в общем случае имеем условие прилипания.

На границе пограничного слоя продольные скорости обоих компонент становятся равными .

Обе компоненты непрерывно отсасываются вдоль всей обтекаемой стенки.

Пусть нормальные составляющие компонент обоих сред на пластинке будут постоянными и соответственно равны (однородное отсасывание), причем если производится отсасывание (при вдуве ).

Рассмотрим пограничным слой вдали от переднего среза пластинки. Определим окончательное распределение скоростей, достигаемой при отсасывании на пластинке бесконечной протяженности.

Условием того, что достигнут конечный профиль будет:

Уравнение неразрывности даёт:

так как на стенке то и всюду внутри пограничного слоя будет ()

, так как на границе пограничного слоя перепада давления нет.

Уравнения пограничного слоя приведется к виду:

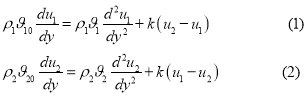
Граничными условиями будут:

при

на границе слоя при

Касательное напряжение на стенке находится по формуле:

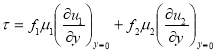
Складывая (1) и (2), получим:

Проинтегрируем один раз:

При

Поэтому

Следовательно,

На стенке

Получаем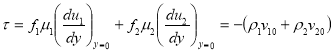

Воспользовавшись первым интегралом, нахождение и можно свести к решению одного линейного дифференциального уравнения третьего порядка с постоянными коэффициентами:

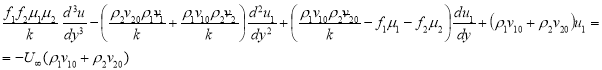
При заданных числовых значениях параметров течения это уравнения решается известными методами.

Граничными условиями будут:

при ;

при .

Это решение применимо для продольного обтекания пластинке с однородным отсасыванием только начиная с некоторого расстояния от передней кромки.

Получаемый из решения профиль скоростей достигается только асимптотически- после того как течением будет пройден вдоль пластинки определенный начальный участок.

Сопротивление не зависит от вязкости, что имеет место также и для случая однородной жидкости, разобранном Т. Шлихтингом. Это есть так называемы сопротивление стока или сопротивление поглощения. Для местного коэффициента сопротивления (для одной стороны пластинки) получаем формулу: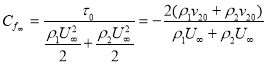

Для случая компонент в тех же предположениях легко получить аналогичные результаты.

Уравнения пограничного слоя в случае компонент

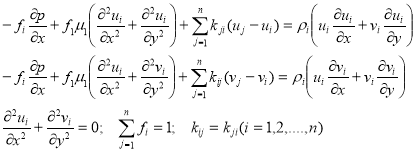
Асимптотическое уравнение для компонента будет:

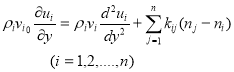
коэффициент взаимодействия между и компонентами, участвующими в движении, формула для сопротивления записывается в виде .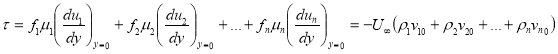

Литература:

1. Н. Е. Кочин, И. А. Кибель. Н. В. Розе. «Теоретическая гидромеханика» ч. I, ч II, ОГИЗ
2. Г.Шлихтинг. «Теория пограничного слоя» М. ИЛ — 1950 г.
3. Х. А. Рахматулин «Аэродинамика проницаемого тела» Вестник МГУ 1950г. № 3.
4. Л. Г. Лайцянский «Ламинарный пограничный слой» Москва 1962 г.
5. Н. А. Слезкин «Динамика вязкой не жеймаемой жидкости». Москва 1953 г.