Задача: Доказать, что треугольник прямоугольный, если его медиана равна половине стороны, к которой она проведена.
Цель урока:
- Повторение изученного материала через поиск различных способов доказательства.
- Развитие творческого подхода к решению задачи.
- Учить мыслить самостоятельно и быть оппонентом одноклассникам.
Подготовка урока
Класс разбит на 5 групп. В группах учащиеся с разным уровнем математической подготовки. Группы по своей силе приблизительно равны. В каждой группе консультант из числа сильных учеников, хороший организатор, который мог бы оказать помощь одноклассникам, обобщить результаты работы группы.
Текст задачи даётся за две недели до проведения урока. Неделю они самостоятельно над ней работают дома. Затем группы работают вместе. Выясняется, кто каким способом решал, проверяется правильность решения. Консультант предварительной отметкой оценивает вклад каждого ученика своей группы, отбирает разные варианты решения, предложенные группой.
На следующем этапе работа проводилась с консультантами. За 3 дня до проведения урока все консультанты были собраны вместе. После того, как были выбраны все различные способы решения, за каждой группой закрепляется защита того или иного способа решения (по 2–3 на группу). Консультанты поручают оформление и защиту того или иного способа решения ученикам из своей группы. (Можно предложить одним подготовку презентации одного из способов решения, а другим её защиту). Всё это учитывается при выставлении окончательной оценки.
Один из способов, например, векторный учитель приготовит для коллективной работы на уроке. Для защиты на уроке способы решения были выбраны в той последовательности, в которой изучается в школьном курсе геометрии материал, используемый в доказательстве.
Ход урока
Урок начался с того, что выяснили, почему будем доказывать, что именно ∠ С будет прямым, а не углы ∠ А или ∠ В.
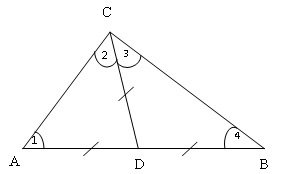

Затем начинается защита учениками способов решения.
На доске закрепляется соответствующий чертёж.
I способ
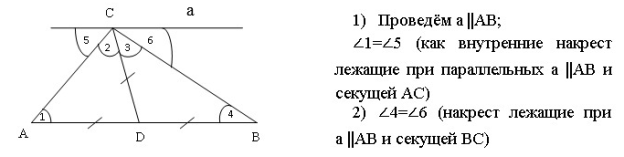
Итак, ∠5=∠2 и ∠6=∠3,
СА и СВ — биссектрисы смежных углов, а биссектрисы смежных углов перпендикулярны⇒∠ С=90 ч.т.д.
II способ
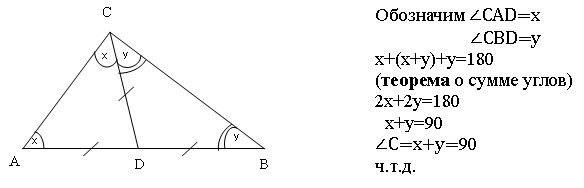
III способ (способ от противного)
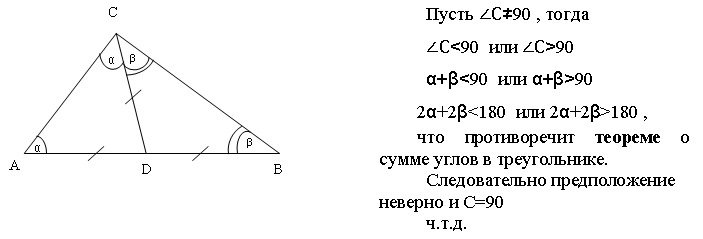
IV способ
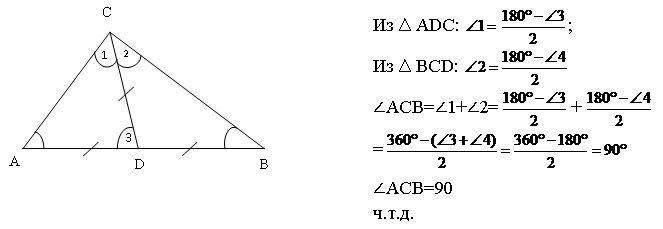
V способ
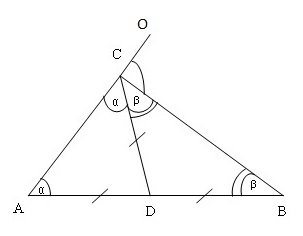

VI способ
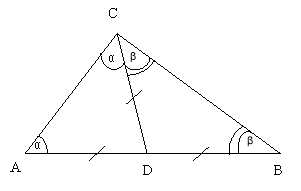
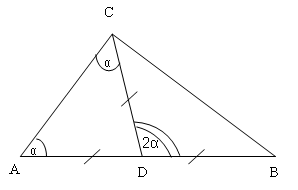
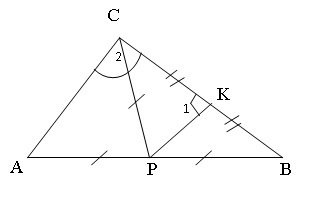
VII способ

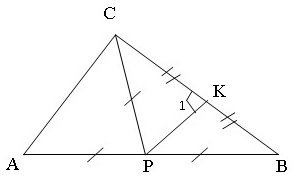
VIII способ (по предыдущему чертежу)

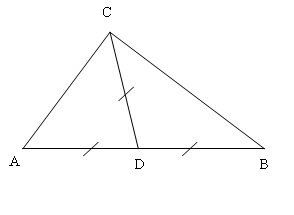
IX способ

X способ
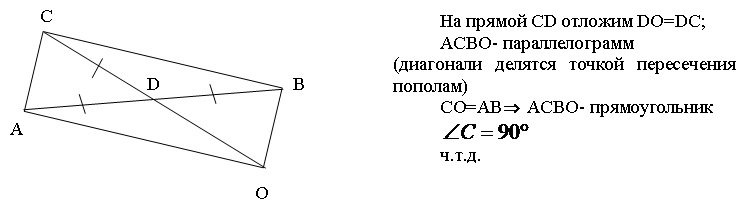
XI способ
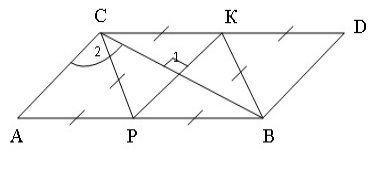

XII способ
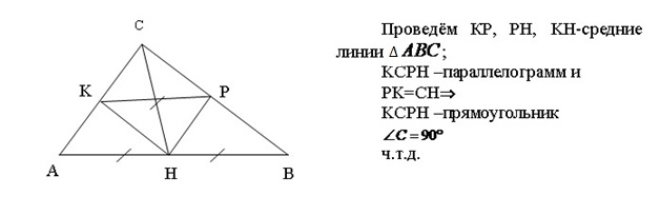
XIII способ
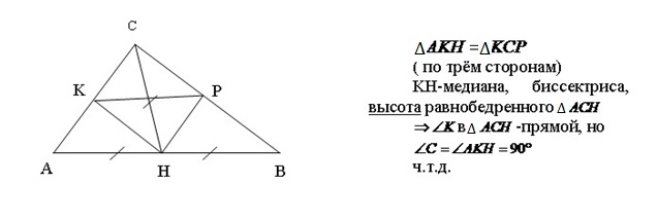
XIV способ

XV способ

Далее с классом записывается решение задачи с применением векторов.
XVI способ
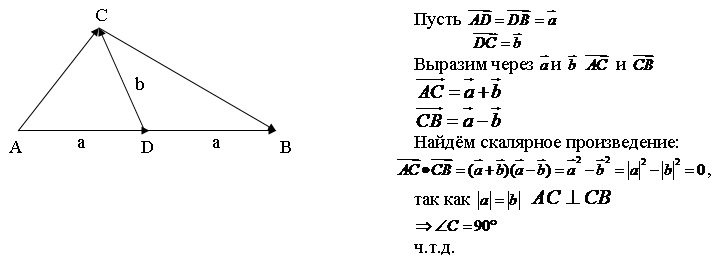
После того, как выслушаны все способы решения задачи, выбираются рациональные пути доказательства. Один из них записывается в тетради.
Что же повторили на уроке? (Заранее записать на доске)
1) Понятие смежных углов и их свойства
2) Метод прямого доказательства и метод от противного
3) Признаки равенства треугольников
4) Определение равнобедренного треугольника, свойства его углов при основании и свойства высоты, проведённой к основанию.
5) Признаки параллельности прямых
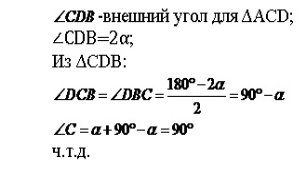
6) Теорема осумме углов треугольника
7) Внешний угол треугольника и его свойства
8) Вписанный угол, измерение вписанных углов
9) Параллелограмм и его свойства
10) Прямоугольник и его свойства
11) Средняя линия треугольника и её свойства
12) Ромб и его свойства
13) Теорема Пифагора
14) Преобразование подобия и его свойства
15) Правила сложения и вычитания векторов
16) Скалярное произведение векторов
17) Теорема косинусов
18) Сумма внутренних углов треугольника
Консультанты выставляют окончательные оценки.







