Предлагается более подробно показать порядок расчета усиления железобетонного элемента на основе нелинейной деформационной модели с присоединением стальных элементов, в данном случае металлических уголков.
В основе данного расчета есть первоначальные допущения, предпосылки нелинейной деформационной модели при различных модификациях выражений, которые определяют различные характеристики сечения (например, жесткость), нормального к продольной оси элемента. Жесткостные характеристики учитывают площадь стальной арматуры, ее положение в поперечном сечении, физико-механические свойства бетона и стальной арматуры. Осуществление такого расчета желательно проводить при помощи метода итераций с последующим приближением окончательного результата вычислений. Преимущества применения нелинейной деформационной модели состоит в том, что существует возможность применения новейших компьютерных технологий при ведении расчетов, а также непосредственное использование диаграмм деформирования бетона и стали арматуры без включения дополнительных упрощений и допущений.
Цель. Представление подробного расчета железобетонного элемента, усиленного присоединением стальных элементов (уголков), на основе нелинейной деформационной модели.
Ключевые слова: усиление, усиливающий элемент, железобетонный элемент, деформационная модель, поперечное сечение, деформации, элементарный участок
Данный расчет основан на диаграммном методе, использующимся при проектировании, а также проведении научных исследованиях [2, 3]. Сам диаграммный метод основан на диаграммах деформирования материалов. Эти диаграммы используются не только на территории Российской Федерации, но и за рубежом.
В сводах правил по проектированию железобетонных конструкций отмечено, что расчет усиление железобетонных конструкций производят согласно общим правилам расчета железобетонных конструкций.
Базовая основа «воспроизводства» нелинейной модели деформаций представляет собой условное разбиение определенного расчетного сечения, нормального к продольной оси элемента, на элементарные участки насколько это возможно для ведения расчетов малой площади. Такое разделение служит для получения более точных значений деформаций на каждом участке, т. е. определить численное распределение деформаций по сечению. Деформации на каждом условном участке разделенного сечения распределяются по линейному закону, что говорит о справедливости гипотезы плоских сечений.
Для определения деформаций на каждом участке в общем случае необходимо обладать следующими данными:
-
Значение начальных деформаций
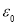 ;
;
-
Значение кривизны
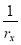 ;
;
- Численное значение центра тяжести определенного участка разделенного сечения.
Первые две составляющие в перечне необходимых данных определяются путем решения системы уравнений:
![]()
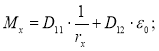
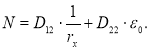
где Mx — изгибающий момент относительно оси x, возникающий в рассматриваемом элементе; N — продольная сила; D11, D12, D22 — жесткости, которые зависят от площади участка, координаты центра тяжести, модуля упругости.
Жесткости в общем случае бывают трех видов:
- Изгибная жесткость плоскости изгиба, определяющаяся по формуле 1:
![]() (1)
(1)
- Жесткость, которая обусловлена влиянием приращения момента на удлинение (или укорочение) продольной оси, определяющаяся по формуле 2:
![]() (2)
(2)
- Жесткость, связанная с удлинением (или укорочением) элемента, определяющаяся по формуле 3:
![]() (3)
(3)
При расчете усиливаемых железобетонных элементов выражения характеристик жесткости ![]() состоят из трех составляющих, которые учитывают бетон и арматуру усиливаемого элемента (по площадям участков бетона
состоят из трех составляющих, которые учитывают бетон и арматуру усиливаемого элемента (по площадям участков бетона ![]() и стали арматуры
и стали арматуры ![]() ), а также металл присоединенных стальных элементов (уголков)
), а также металл присоединенных стальных элементов (уголков) ![]() [5]. Приведенные обозначения сохраняют единство с нормативными документами [1], индекс a несет информацию об усиливающей конструкции «каркас из стальных уголков» (рисунок 1).
[5]. Приведенные обозначения сохраняют единство с нормативными документами [1], индекс a несет информацию об усиливающей конструкции «каркас из стальных уголков» (рисунок 1).
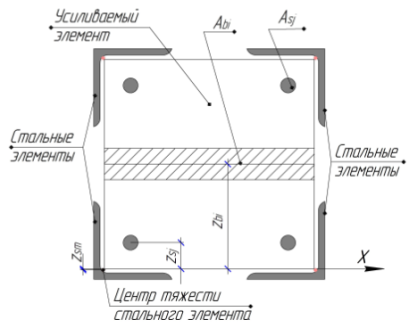
Рис. 1. Расчетная схема нормального сечения железобетонного элемента, усиленного присоединением стальных элементов (уголков)
Нумерация условных участков бетона ведется с индексом i, арматуры с индексом j, а усиливающего стального элемента m.
Возможность видоизменения записи выражений для расчета численного значения жесткости ![]() (в общем случае i, j — 1, 2) предопределяет широту применения нелинейной деформационной модели, основываясь на диаграммах деформирования материалов [4].
(в общем случае i, j — 1, 2) предопределяет широту применения нелинейной деформационной модели, основываясь на диаграммах деформирования материалов [4].
Третья позиция в перечне необходимых данных для определения значений деформаций по «раздробленному» сечению определяется расстоянием между центром тяжести элементарного участка и выбранной горизонтальной осью, как правило, нижней гранью рассматриваемого комплексного элемента. Определение центра тяжести элемента в общем случае представлено на рисунке 1.
Данные величины определяются «структуру» как усиливаемую, так и усиливающую составляющие расчетного комплексного сечения.
Как было указано выше осуществление данного расчета, то есть расчета с применением деформационной модели, рекомендуется проводить с использованием итерационного метода с учетом дальнейшего приближения окончательного результата вычислений. Диаграммный метод выполняется путем постепенного итерационного уточнения коэффициентов упругопластических деформаций материалов по элементарным участкам разбиения, при этом контролируя результаты по численным значениям величин деформаций на каждом элементарном участке ![]() .
.
Вывод: рассмотренный (более подробный) порядок расчета усиления железобетонных конструкций путем присоединения стальных элементов (уголков) не утрачивает все свои первоначальные преимущества модели деформаций, а именно учет нелинейных свойств материалов через диаграммы деформирования составляющих комплексного сечения (бетона, стальной арматуры), и определяются уровнем относительных деформаций; возможность упрощения ведения расчетов; оценка усиливаемой железобетонной (комплексной) конструкции по двум группам предельных состояний (по несущей способности и пригодности к эксплуатации).
Литература:
- СП 63.13330.2012. Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52–01–2003.
- Ерышев В. А., Тошин Д. С., Бондаренко А. С., Саратов Н. В., Тихонова Е. П. Диаграммный метод оценки деформаций изгибаемых железобетонных элементов при разгрузке // Вестник Волжского регионального отделения Российской академии архитектуры и строительных наук. — 2009. — № 12. — С. 182–188.
- Тошин Д. С., Анисимова М. П. Поиск оптимального способа реализации итерационного приближения при расчете по деформационной модели // Научное обозрение. — 2016. — № 17. — С. 25–29.
- Тошин Д. С. Прикладные возможности деформационной модели железобетона // Молодой ученый. — 2016. — № 29 (133). — С. 164–166;
- Журавлёва Т. А. Применение диаграммного метода расчета при усилении железобетонных элементов присоединением стальных элементов //Молодой ученый. — 2017. — № 10 (144) — С. 59–61







