В данной статье предлагается разработка урока алгебры в 7 классе по учебнику А. Г. Мордковича. Школьникам скоро предстоит сдавать экзамены, и многие из них хотят, как можно хорошо и быстро научиться решать задачи. И в таких случаях можно применять нестандартные решения. Задания: «Решить систему уравнений» входят в задания экзамена как после 9 класса, так и после 11 класса. Данное изучение лучше применить на втором уроке в теме «Решение систем уравнений способ сложения».
Цель: Познакомиться с нестандартным решением систем линейных уравнений.
Задача: Научиться решать системы линейных уравнений методом Крамера и сравнить с другими методами решения.
Ход урока
- Сегодня на уроке мы рассмотрим нестандартный способ решения систем уранений с двумя переменными и сравним данный способ решения с другими решенями. Но сначала повторим темы прошлых уроков:
– Что значит «решить систему линейных уравнений»? (Найти все его корни, или показать, что их нет.)
– Что является решением системы с двумя переменными? (Пара значений переменных, обращающая каждое уравнение системы в верное равенство.)
– Какие способы решения систем уравнений мы применяли? (способ сравнения; графический способ; способ подстановки; способ сложения)
К доске вызываются четыре ученика и решают систему различными способами, а остальные по вариантам. После решения ученики рассказывают алгоритм решения, в случае затруднения помогает класс.
![]()
- При решении систем уравнений с двумя переменными можно применить еще один способ, применяя метод Крамера. Габриэль Крамер (Gabriel Cramer) (31.07.1704 — 04.01.1752). Швейцарский математик, один из создателей линейной алгебры.
Данный метод значительно ускоряет процесс решения систем линейных уравнений и очень удобно применять его для систем с громоздкими вычислениями.
Метод Крамера применяется в Высшей математике при решении системы линейных уравнений с тремя неизвестными или решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Вам будет интересно научиться применять решение, не просто школьного курса, а решение, которые применяют студенты первых курсов высших заведений.
В данном методе при решении используют понятие определителя системы:
Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается Δ(дельта) и вычисляется по формуле.
![]()
где, ![]() ,
, ![]() — заданные числа; х и у- неизвестные, числа
— заданные числа; х и у- неизвестные, числа ![]() — называются коэффициентами, а числа
— называются коэффициентами, а числа ![]() — свободными членами.
— свободными членами.
Δ = ![]() = а11 · а22 — а12 · а21.
= а11 · а22 — а12 · а21.
Для нахождения неизвестных н6ам нужно найти еще два определителя ![]() и
и ![]() , путём замены коэффициентов при соответствующих неизвестных свободными членами:
, путём замены коэффициентов при соответствующих неизвестных свободными членами:
![]() =
= ![]() = в1 · а22 — а12 · в2.
= в1 · а22 — а12 · в2.
![]() = а11 · в2 — в1 · а21.
= а11 · в2 — в1 · а21.
Формула Крамера для нахождения неизвестных: ![]() х =
х = ![]() ; у =
; у = ![]() .
.
Найти значения неизвестных можно только при условии, когда определитель не равен нулю (Δ≠0).
Замечание: если определитель системы равен нулю, то система может иметь бесконечно много решений или не имеет решений.
Пример:
![]()
Δ = ![]() = 3·4–2·5 = 12–10=2≠0
= 3·4–2·5 = 12–10=2≠0
Найдем еще два определителя ![]() и
и ![]() , путём замены коэффициентов при соответствующих неизвестных свободными членами:
, путём замены коэффициентов при соответствующих неизвестных свободными членами:
![]() =
= ![]() 2;
2;
![]()
Формула Крамера для нахождения неизвестных: х = ![]() ; у =
; у = ![]() . Ответ: (1;-2).
. Ответ: (1;-2).
- Решите систему уравнений способ сложения и методом Крамера:
а) ![]() ; б)
; б) ![]() ; в)
; в) 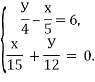
Решив системы, сделаем вывод: какой способ решается быстрее и легче?
– способ сравнения: выразим переменную у через х, решим уравнение через х, приравняв правые части уравнения, и найдем переменную у;
– графический способ: выразим переменную у через х, построим график. Но на графике не всегда можно увидеть точное решение;
– способ подстановки: выразим одну переменную через другую, подставим и решим уравнение, найдем другую переменную;
– способ сложения: умножим уравнения системы на такие множители, чтобы коэффициенты при одной из переменных стали противоположными; сложим левые и правые части уравнений системы; решим получившееся уравнение с одной переменной и найдем другую переменную;
– методом Крамера: по формулам найдем три определителя и переменные.
При рассмотрении решений несколькими способами ученики убеждаются, что метод Крамера упрощает время и трудности вычисления для нахождения неизвестных в решении систем уравнений.
- Итоги урока:
— Сегодня на уроке мы обобщили все методы решения систем линейных уравнений с двумя переменными.
— Какие способы решения вы знаете?
— Каким бы способом вы решали системы уравнений и почему?
— А какой способ решения вы бы применили на экзамене?
- Домашнее задание: 1225(а, б), 1226.
Литература:
1. Ю. Н. Макарычев, Н. Г. Миндюк, К.И. и др. Алгебра 7 класс. Учебник. –М.: Просвещение 3-е изд. — М.: 2014. — 256 с.
- Письменный Д. Т. Конспект лекций по высшее математике. 1 часть.- второе издание, испр.- М: Айрис-пресс, 2003.-288с.: ил.
- Лисичкин В. Т., Соловейчик И. Л. математика: учебное пособие для техникумов. -М.: Высшая школа, 1991 480 с: ил.
- Пичурин Л. Ф. За страницами учебника алгебры. — М: Просвещение, 1990–224с., ил.







