Приведен расчет объемного конечного элемента четырехугольной формы поперечного сечения при различных вариантах аппроксимации перемещений.
Ключевые слова: Четырехугольный конечный элемент, полином, матрица-строка, производные узловых перемещений, аппроксимация.
Узловые неизвестные и аппроксимация перемещений.
В каждом узле конечного элемента в качестве узловых неизвестных принимаются перемещения и их первые производные. Столбец узловых неизвестных в глобальной системе координат имеет вид
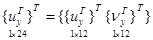 , (1)
, (1)
где
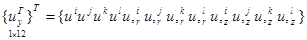 ;
;
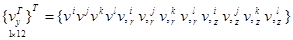 ; (2)
; (2)
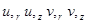 - производные перемещений в радиальном и осевом направлениях по глобальным координатам r и z.
- производные перемещений в радиальном и осевом направлениях по глобальным координатам r и z.
Вектор узловых неизвестных рассматриваемого конечного элемента в локальной системе координат представляется аналогично
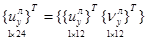 , (3)
, (3)
где
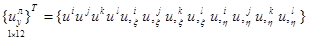 ;
;
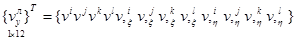 ; (4)
; (4)
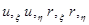 - производные перемещений радиального и осевого перемещений в локальной системе координат
- производные перемещений радиального и осевого перемещений в локальной системе координат 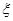 и η.
и η.
Ввиду того, что между глобальными и локальными координатами существует связь, то на ее основе можно производные функций в одной системе выразить через производные функций в другой системе
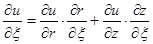 ;
; 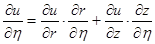 ;
;
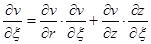 ;
; 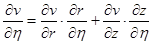 . (5)
. (5)
На основании выражений (5) можно сформировать матричные соотношения между векторами узловых перемещений
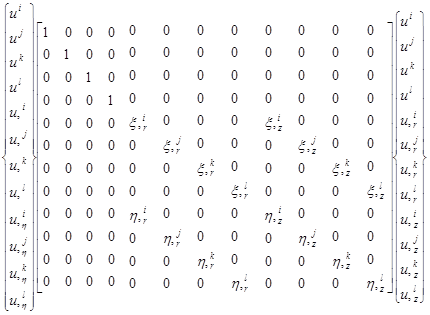 (6)
(6)
и представить их в компактном виде
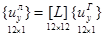 ;
; 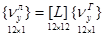 . (7)
. (7)
С использованием (7) формируется матричное соотношение между полными векторами узловых неизвестных конечного элемента в локальной и глобальной системах координат
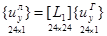 , (8)
, (8)
где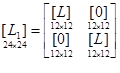 .
.
Перемещения внутренней точки конечного элемента определяются через векторы узловых перемещений в локальной системе координат с использованием аппроксимирующих функций
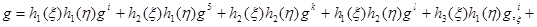
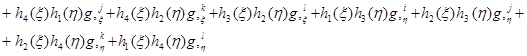 (9)
(9)
Здесь под символом q понимается радиальное перемещение u или осевое перемещение ν, а функции 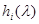 представляют собой полиномы Эрмита, определяемые формулами
представляют собой полиномы Эрмита, определяемые формулами
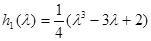 ;
; 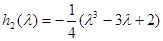 ;
;
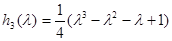 ;
; 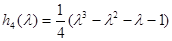 , (10)
, (10)
где символом λ обозначается локальная координата 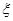 или η.
или η.
Для представления аппроксимирующих выражений в матричной форме введем обозначение матрицы-строки полиномов Эрмита в виде
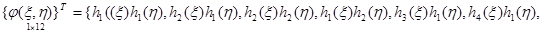
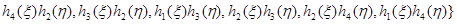 . (11)
. (11)
С использованием (11) радиальное и осевое перемещения z внутренней точки конечного элемента определяются матричными соотношениями
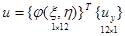 ;
; 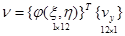 , (12)
, (12)
а вектор-столбец перемещений внутренней точки дискретного элемента можно представить в виде
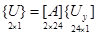 , (13)
, (13)
где матрица [A] имеет вид
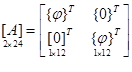 Производные перемещений внутренней точки конечного элемента в глобальной системе координат r, z получаются дифференцированием выражений (12)
Производные перемещений внутренней точки конечного элемента в глобальной системе координат r, z получаются дифференцированием выражений (12)
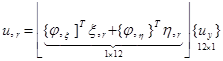 ;
;
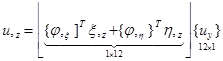 ;
;
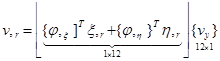 ;
;
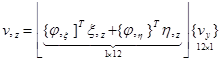 . (14) Деформации внутренней точки конечного элемента могут быть выражены через узловые неизвестные в матричном представлении
. (14) Деформации внутренней точки конечного элемента могут быть выражены через узловые неизвестные в матричном представлении
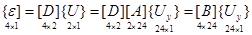 , (15)
, (15)
где матрица [B] имеет вид
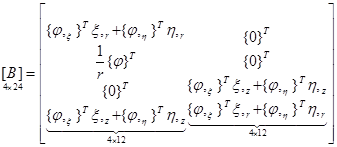 . (16)
. (16)
Литература
1. Оден Дж. Конечные элементы в нелинейной механике сплошных сред. Пер. с англ. М.: Мир, 1976, 464 с.
2. Самуль В.И.Основы теории упругости и пластичности. М.: «Высшая школа, 1970, 288 с.
3. Постнов В.А., Хархурим И.Я. Метод конечных элементов в расчетах судовых конструкций. Л.: Судостроение, 1974, 344 с.







