In given work the inverse edge task with integral conditions for hyperbolic equation of second order is researched. First of all the initial task is brought together to equivalent task, in which the theorem of existence and unique solution is proved. Further, having used these facts, existence and unity of classical solution of initial task is proved too.
Рассмотрим уравнение
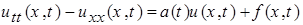 (1)
(1)
в области 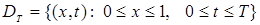 и поставим для него обратную краевую задачу с начальными условиями
и поставим для него обратную краевую задачу с начальными условиями
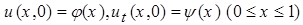 , (2)
, (2)
нелокальными условиями
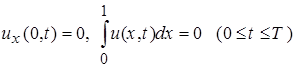 (3)
(3)
и дополнительным условием
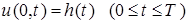 , (4)
, (4)
где 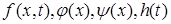 - заданные функции, а
- заданные функции, а 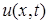 ,
, 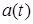 - искомые функции.
- искомые функции.
Смешанные задачи для гиперболических уравнений с нелокальными интегральными условиями были ранее рассмотрены в работах [1, 2].
Определение. Классическим решением задачи (1)-(4) назовём пару 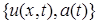 функций
функций 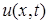 и
и 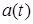 , обладающих следующими свойствами:
, обладающих следующими свойствами:
1) функция 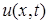 непрерывна в
непрерывна в 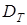 вместе со всеми своими производными, входящими в уравнение (1);
вместе со всеми своими производными, входящими в уравнение (1);
2) функция 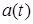 непрерывна на
непрерывна на 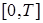 ;
;
3) все условия (1)-(4) удовлетворяются в обычном смысле.
Аналогично [3] можно доказать следующую лемму.
Лемма 1. Пусть
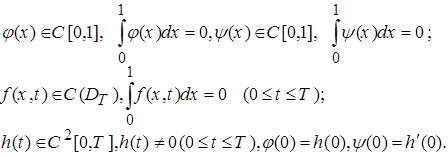
Тогда задача нахождения классического решения задачи (1)-(4) эквивалентна задаче определения функций 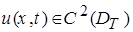 и
и 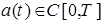 из (1),(2) и
из (1),(2) и
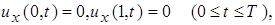 (5)
(5)
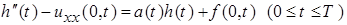 . (6)
. (6)
С целью исследования задачи (1), (2), (5), (6) рассмотрим следующие пространства. Обозначим через 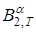 [4] совокупность всех функций вида
[4] совокупность всех функций вида
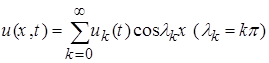 ,
,
рассматриваемых в 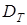 , где каждая из функций
, где каждая из функций 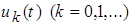 непрерывна на
непрерывна на 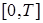 и
и
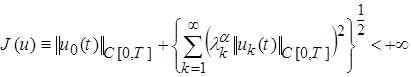 ,
,
причем 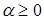 . Норму в этом множестве определим так:
. Норму в этом множестве определим так:
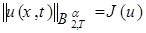 .
.
Через 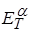 обозначим пространство
обозначим пространство 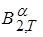
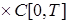 вектор-функций
вектор-функций 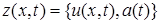 с нормой
с нормой
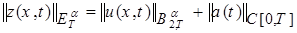 .
.
Известно, что 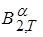 и
и 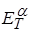 являются банаховыми пространствами.
являются банаховыми пространствами.
Первую компоненту 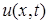 классического решения
классического решения 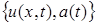 задачи (1),(2),(5),(6) будем искать в виде:
задачи (1),(2),(5),(6) будем искать в виде:
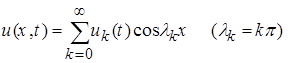 , (7)
, (7)
где
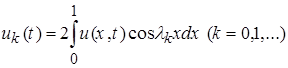 .
.
Тогда, применяя формальную схему Фурье, из (1) и (2) имеем:
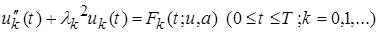 , (8)
, (8)
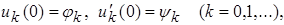 (9)
(9)
где
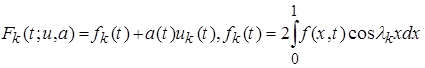 ,
,
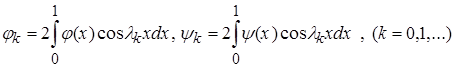 .
.
Из (8),(9) находим:
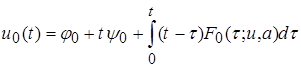 , (10)
, (10)
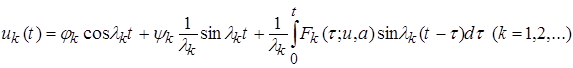 . (11)
. (11)
Очевидно, что
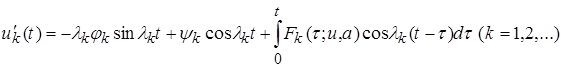 , (12)
, (12)
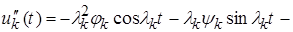
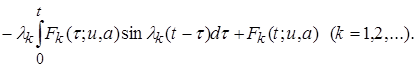 (13)
(13)
После подстановки выражений 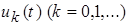 в (7), для определения компоненты
в (7), для определения компоненты 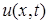 классического решения задачи (1),(2),(5),(6) получаем:
классического решения задачи (1),(2),(5),(6) получаем:
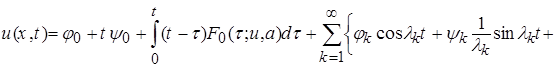
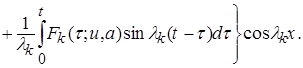 (14)
(14)
Теперь, из (6), с учетом (7), имеем:
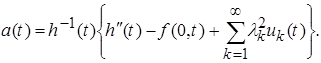 (15)
(15)
Для того, чтобы получить уравнение для второй компоненты 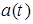 классического решения
классического решения 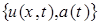 задачи (1),(2),(5),(6) подставим выражение (11) в (15):
задачи (1),(2),(5),(6) подставим выражение (11) в (15):
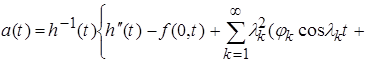
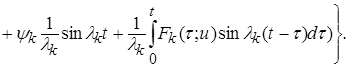 (16)
(16)
Таким образом, решение задачи (1),(2),(5),(6) свелось к решению системы (14), (16) относительно неизвестных функций 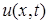 и
и 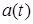 .
.
Исходя из определения классического решения задачи (1), (2), (5), (6) доказывается следующая
Лемма 2. Если 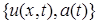 - любое классическое решение задачи (1), (2), (5), (6), то функции
- любое классическое решение задачи (1), (2), (5), (6), то функции
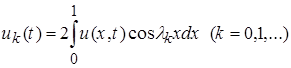
удовлетворяют системе (10),(11).
Теперь , из (11)-(13) имеем:
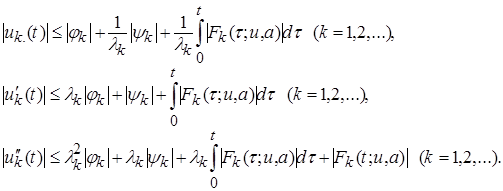
Отсюда имеем:
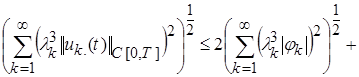
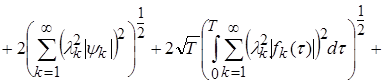
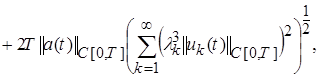 (17)
(17)
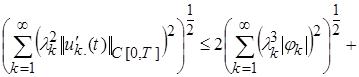
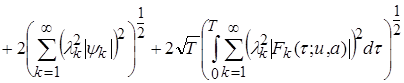 , (18)
, (18)
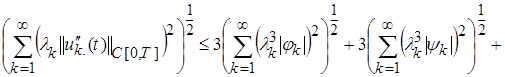
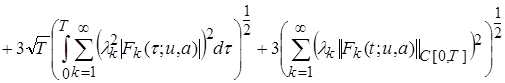 . (19)
. (19)
Предположим, что данные задачи (1),(2),(5),(6) удовлетворяют следующим условиям:
1. 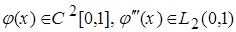 и
и 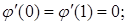
2. 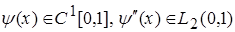 и
и 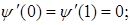
3. 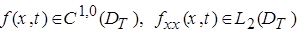 и
и 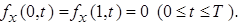
Тогда из (17)-(19), (10) соответственно получаем:
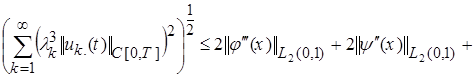
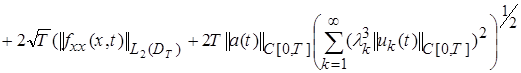 , (20)
, (20)
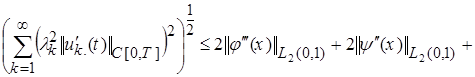
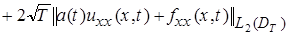 , (21)
, (21)
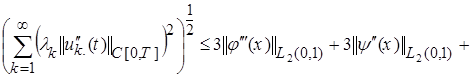
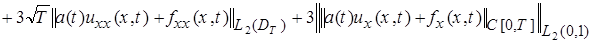 , (22)
, (22)
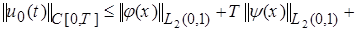
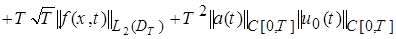 . (23)
. (23)
Далее, из (20) и (23) находим:
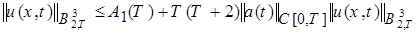 , (24)
, (24)
где
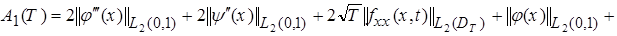
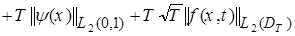 .
.
Теперь из (15), с учётом (20), имеем:
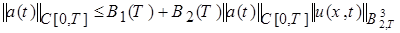 , (25)
, (25)
где
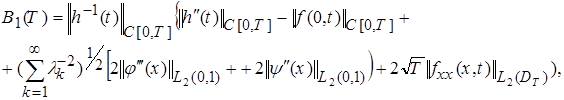
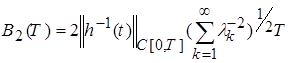 .
.
Из неравенств (24) и (25) заключаем:
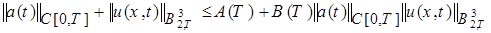 , (26)
, (26)
где
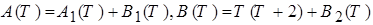 .
.
Итак, можно доказать следующую теорему.
Теорема 1. Пусть выполнены условия 1-3 и
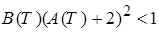 . (27)
. (27)
Тогда задача (1),(2),(5),(6) имеет в шаре 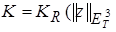
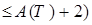 из
из 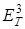 единственное решение.
единственное решение.
Доказательство. В пространстве 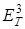 рассмотрим уравнение
рассмотрим уравнение
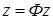 , (28)
, (28)
где 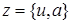 , компоненты
, компоненты 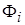 оператора
оператора 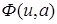 определены правыми частями уравнений (14), (16) соответственно. Рассмотрим оператор
определены правыми частями уравнений (14), (16) соответственно. Рассмотрим оператор 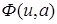 в шаре
в шаре 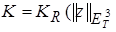
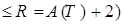 из
из 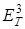 .
.
Аналогично (26) получаем, что для любых 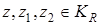 справедливы оценки:
справедливы оценки:
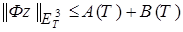
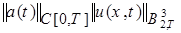 , (29)
, (29)
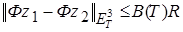
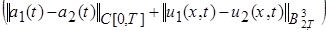 . (30)
. (30)
Тогда из оценок (29) и (30), с учетом (27), следует, что оператор Ф действует в шаре 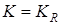 и является сжимающим. Поэтому в шаре
и является сжимающим. Поэтому в шаре 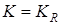 оператор Ф имеет единственную неподвижную точку
оператор Ф имеет единственную неподвижную точку 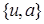 , которая является решением уравнения (28).
, которая является решением уравнения (28).
Функция 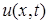 , как элемент пространства
, как элемент пространства 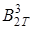 , непрерывна и имеет непрерывные производные
, непрерывна и имеет непрерывные производные 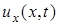 ,
, 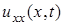 в
в 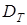 .
.
Из неравенств (21), (22) следует, что 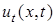 ,
, 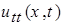 непрерывны в
непрерывны в 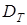 .
.
Легко проверить, что уравнение (1) и условия (2), (5), (6) удовлетворяются в обычном смысле. Значит, 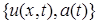 является классическим решением задачи (1),(2),(5),(6), а в силу леммы 2 это решение единственно. Теорема доказана.
является классическим решением задачи (1),(2),(5),(6), а в силу леммы 2 это решение единственно. Теорема доказана.
С помощью леммы 1 легко доказывается следующая
Теорема 2. Пусть выполняются все условия теоремы 1 и
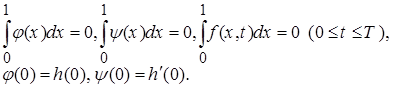 .
.
Тогда задача (1)-(4) имеет в шаре 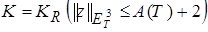 из
из 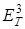 единственное решение.
единственное решение.
Литература:
1. Гордезиани Д.Г., Авалишвили Г.А. // Мат. Моделирование, 2000, т.12, №1, с. 94-103.
2. Пулькина Л.С. Нелокальная задача с интегральными условиями для гиперболического уравнения // Дифференц. Уравнения, 2004, т.40, №7, с. 887-892.
3. Намазов Г.К., Мегралиев Я.Т. Исследование классического решения одномерной обратной краевой задачи для полулинейных псевдогиперболических уравнений высокого порядка//Вестник Бакинского Университета, серия физико-математических наук, 2003, №2, с.5-15.
4. Худавердиев К.И. К теории многомерных смешанных задач для нелинейных гиперболических уравнений // Докт. Дис. Физ.-матем. Наук, Азерб. Гос. Унив., Баку, 1973, 319 с.







