Важным элементом в управлении общественными процессами являются демографические прогнозы. В настоящее время очень трудно найти какую-либо область экономики или социальной жизни, где бы при долгосрочном планировании не использовались их результаты.
В решении задачи построения перспективных расчетов численности полезным является математическое моделирование. Разработка и использование разного рода математических моделей служат как для анализа воспроизводства населения в целом, так и для выявления закономерностей развития тех или иных демографических процессов. При моделировании принимаются определенные исходные предположения в отношении основных составляющих процесса. На этой основе исчисляются другие характеристики населения и его структуры.
К первым математическим моделям населения относятся детерминированные модели роста человечества, прежде всего это модели линейного и экспоненциального роста [1–2]. Следует отметить, что данные модели дают удовлетворительные результаты только на короткий период, продление же на более длительный срок не дает адекватных результатов.
Наиболее известная детерминированная модель — модель стабильного населения [1, 3–7]. В такой модели население характеризуется неизменными во времени возрастными интенсивностями рождаемости, смертности и возрастной структурой населения. Разработку теории стабильного населения связывают с такими именами как Л. Эйлер, Г. Кнапп, В. Лексис, Дж. Лотка, В. Борткевич, П. Лесли. Большой вклад в разработку методов практического применения стабильного населения внесли советские демографы С. А. Новосельский, В. В. Паевский, А. Я. Боярский, И. Г. Венецкий и др. [7]. Известны непрерывные и дискретные аналоги модели стабильного населения. В основе непрерывных моделей лежит интегральное уравнение воспроизводства населения (уравнение Лотки), в основе дискретных — матричная модель (матрица Лесли).
Современный этап развития теории стабильного населения связывают с обобщением основных выводов на случай демографических процессов с переменными интенсивностями (процессы рождаемости и смертности в виде временных рядов, случайных процессов) — А. Коул [8] и А. Лопес. А также Р. Лии [9], Д. Ахлбург [10], З. Сайкес [11], М. Алхо [12], Б. Спенсер [13], Дж. Поллард [14], Дж. Кохен [15], Н. Кейфица [16], Х. Касвелл [17], Л. Гудман [18] и другие [7].
В конце XIX века учеными была предпринята попытка использовать в качестве модели, описывающей рост человечества, логистическую кривую [1, 3–4, 7, 19]. Этой модели придерживались Р. Пирль и Л. Рид [19]. Следует отметить, что попытки Р. Пирля и других демографов использовать логистическую кривую для прогнозирования численности населения в будущее привели к ненадежным и неправильным выводам. Логистическая кривая может быть полезной лишь при краткосрочном прогнозе численности населения, а также как приближение динамики некоторых демографических показателей, например рождаемости, смертности, функции дожития и т. д.
Еще одной детерминированной моделью воспроизводства населения является модель гиперболического изменения численности населения. Впервые предположение, что скорость роста численности населения пропорциональна квадрату численности, было отмечено в 1960 г. Хайнцом фон Ферстером, П. Мором и Л. Амиотом [7]. По этой же формуле И. С. Шкловский прогнозировал численность населения земного шара в период с 1600 по 1960 г. [1]. В настоящее время в этом направлении работает С. П. Капица [20].
Значительный вклад в математическую демографию сделан О. В.Староверовым [21]. Староверовов О. В. рассматривал демографические процессы в виде марковских моделей в форме цепей Маркова. Староверовым О. В. получены модели миграции, межотраслевого и социального движения населения. Модели естественного движения населения исследованы в дискретном и непрерывном виде, для них в [21] получены основные уравнения. В [21] Староверовым О. В. предложена стохастическая модель развития населения с дискретным временем, учитывающая случайность, как в рождаемости, так и в смертности.
Заметим, что соотношения для модели естественного движения населения в дискретном времени (матричная модель — матрица Лесли), полученные также О. В. Староверовым [21], являются, так называемой передвижкой возрастов [1, 22], то есть применение подхода Лесли приводит к тем же результатам, что и метод передвижки по возрастам. А модель Лотки есть не что иное, как аналог метода передвижки в непрерывном времени.
Метод компонент или метод передвижки разработан П. К. Уэлптоном [22]. В этом методе за основу принимают распределение населения по возрастам и постепенно передвигают численности отдельных возрастных групп в соответствии с показателями таблиц смертности. В России перспективными исчислениями населения методом возрастных передвижек занимались С. Г. Струмилин, А. Я. Боярский, П. П. Шушерин, М. С. Бедный [7], а в последнее время Государственный комитет Российской Федерации по статистике, Центр демографии и экологии человека, Отдел населения ООН, Международный Институт прикладного системного анализа (IISA) в г. Лаксенбург (Австрия).
Приведенный анализ множества моделей показывает, что в моделировании демографических процессов наиболее распространены детерминированные модели (дискретные и непрерывные), и стохастические дискретные (имитационные модели). Поскольку реальные процессы развития численности населения протекают в непрерывном времени и являются стохастическими, то актуальным является построение стохастической демографической модели с непрерывным временем. Решению именно этой проблемы и посвящена работа [23], в которой предлагается для прогнозирования демографических процессов применить модели и методы теории массового обслуживания [24].
В работе [23,] предложена математическая модель процесса изменения демографической ситуации в виде автономной немарковской системы массового обслуживания с неограниченным числом приборов. Ее исследование выполнено методами виртуальных фаз и асимптотического анализа стохастической повозрастной плотности численности заявок, обслуживаемых в системе в момент времени t. Найдено распределение вероятностей стохастической плотности численности заявок и основные характеристики, определяющие это распределение. Разработанная модель и методы ее исследования могут быть применены к анализу процесса изменения демографической ситуации в Российской Федерации.
Покажем, что данная математическая модель, достаточно адекватно моделируют процесс изменения возрастной структуры женского населения.
Будем рассматривать группу всех женщин Российской Федерации. Исходя из предположений о динамике суммарного коэффициента рождаемости и используя результаты из [23, 25], а также возможности пакета MathCAD, можно сделать прогнозную оценку демографической ситуации в Российской Федерации. Начальными условиями являются значения численности женщин в 2005 году [26].
Согласно статистическим данным суммарный коэффициент рождаемости в 2005 году составлял 1,294, в 2010 году — 1,567 [26]. В последние годы по причине активно проводимой социальной политики ожидается его повышение до значения 2,4. Идеализируя демографическую ситуацию, будем предполагать увеличение суммарного коэффициента рождаемости до η(t)=2,4 на интервале прогнозирования от 2010 до 2105 года, получены следующие значения средней численности женщин в долгосрочной перспективе (Рис. 1).
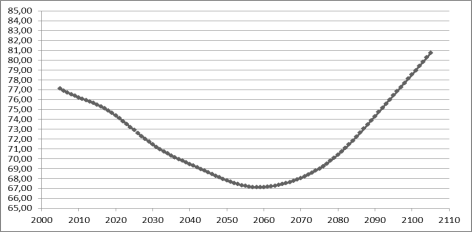
Рис. 1 Сценарий демографической ситуации в период с 2005 года по 2105 год (млн. чел.)
Как видно из рис. 1, в условиях оптимального предположения относительно суммарного коэффициента рождаемости, а именно, что его значение составит 2,4, численность женского населения на рассматриваемом отрезке времени будет продолжать снижаться в течение 50 лет, но, начиная с 2065 года, будет наблюдаться его значительный рост.
Для того чтобы сказать, что сценарий на 2105 год правилен и адекватен, необходимо, чтобы рассчитанные нами значения возрастной структуры населения в 2010 и в 2015 году были наиболее близки к статистическим данным по этим годам. Результаты приведены в таблице 1.
Таблица 1
Сравнение статистических значений численности возрастных групп женщин срассчитанными значениями (млн. чел.)
|
Статистические данные |
Рассчитанные данные |
Статистические данные |
Рассчитанные данные |
|
|
2010 |
2010 |
2015 |
2015 |
|
|
Все население |
76,810 |
76,227 |
78,496 |
75,495 |
|
В том числе в возрасте, лет |
||||
|
0–4 |
3,884 |
3,953 |
4,504 |
4,637 |
|
5–9 |
3,462 |
3,556 |
3,906 |
3,926 |
|
10–14 |
3,225 |
3,171 |
3,475 |
3,531 |
|
15–19 |
4,111 |
4,110 |
3,332 |
3,148 |
|
20–24 |
5,999 |
5,972 |
4,549 |
4,079 |
|
25–29 |
5,972 |
6,016 |
6,241 |
5,922 |
|
30–34 |
5,546 |
5,393 |
6,049 |
5,961 |
|
35–39 |
5,200 |
5,068 |
5,558 |
5,334 |
|
40–44 |
4,766 |
4,719 |
5,213 |
4,998 |
|
45–49 |
5,632 |
5,913 |
4,788 |
4,632 |
|
50–54 |
6,234 |
6,120 |
5,890 |
5,759 |
|
55–59 |
5,670 |
5,496 |
6,099 |
5,884 |
|
60–64 |
4,587 |
4,041 |
5,446 |
5,172 |
|
65–69 |
2,510 |
2,809 |
3,949 |
3,671 |
|
70 и более |
10,011 |
9,880 |
9,487 |
8,841 |
Как видно из представленных в таблице данных, конечно, имеется небольшая погрешность около 5 %, максимальная погрешность наблюдается только в трех возрастных группах, и она составляет не более 10 %.
Предложенная в [23] автономная система массового обслуживания с неограниченным числом приборов и разработанный метод ее исследования, являются эффективным инструментом анализа сложившийся демографической ситуации, а также наблюдения эффективности проводимой политики и прогнозирования будущих динамик демографических процессов.
Литература:
- Венецкий И. Г. Статистические методы в демографии. — М.: Статистика, 1977. — 207 с.
- Kendall D. G. Stochastic processes and population growth [Электронный ресурс] // Journal of the Royal Statistical Society. — 1949. — Vol. 11, N 2. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Демографические модели: сб. статей / под ред. Е. М. Андреева, А. Г. Волкова. — М.: Статистика, 1977. — 182 с.
- Donald T. R. Demographic methods and concepts. — Oxford: Oxford University Press, 2006. — 523 p.
- Hinde A. Demographic methods. — Arnold, 1998. — 305 p.
- Newell C. Methods and models in demography. — Belhaven, 1988. — 217 p.
- Демографический энциклопедический словарь / под ред. Д. И. Валентея. — М.: Советская энциклопедия, 1985. — 608 с.
- Coale А., Trussell J. The development and use of demographic models [Электронный ресурс] // Population Studies. — 1996. — Vol. 50, N 3. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Lee R. Probabilistic approaches to population forecasting [Электронный ресурс] // Population and Development Review. — 1998. — Vol. 24, Supplement: Frontiers of Population Forecasting. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Ahlburg D., Vaupel J. Alternative projections of the U. S. population [Электронный ресурс] // Demography. — 1990. — Vol. 27, N 4. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Sykes Z., Kim J. Dynamics of some special populations with NRR = 1 [Электронный ресурс] // Demography. — 1978. — Vol. 15, N 4. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Alho M., Spencer B. Uncertain population forecasting [Электронный ресурс] // Journal of the American Statistical Association. — 1985. — Vol. 80, N 390. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Pollard J. Continuous–time and discrete–time models of population growth [Электронный ресурс] // Journal of the Royal Statistical Society. — 1969. — Series A, Vol. 132, N 1. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Cohen J. Ergodicity of age structure in populations with Markovian vital rates, III: Finite state moments [Электронный ресурс] // Advances in Applied Probability. — 1977. — Vol. 9, N 3. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Keyfitz N. Introduction to the mathematics of population with revisions. — Wesley Pub. Co, 1977. — 490 p.
- Caswell H. Matrix population models: construction, analysis, and interpretation. — Sunderland, Massachusetts, Sinauer Associates, 1989. — 722 p.
- Goodman L. Stochastic models for the population growth of the sexes growth [Электронный ресурс] // Biometrika. — 1968. — Vol. 55, N 3. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Booth H. Demographic forecasting: 1980 to 2005 in review [Электронный ресурс] // International Journal of Forecasting. — 2006. — N 22. — Электрон. версия печат. публ. — Доступ из базы данных “Sciencedirect”. — URL: http:// www.sciencedirect.com (дата обращения: 19.10.2017).
- Reed L., Pearl L. On the summation of logistic curves [Электронный ресурс] // Journal of the Royal Statistical Society. — 1927. — Vol. 90, N 4. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Капица С. П. Общая теория роста человечества: сколько людей жило, живет и будет жить на земле. — М.: Наука, 1999. — 190 с.
- Староверов О. В. Модели движения населения. — М.: Наука, 1979. — 230 с.
- Whelpton P. K. Population of the United States, 1925 to 1975 [Электронный ресурс] // The American Journal of Sociology. — 1928. — Vol. 34, N 2. — Электрон. версия печат. публ. — Доступ из базы данных “Jstor”. — URL: http://www.jstor.org (дата обращения: 19.10.2017).
- Носова М. Г. Автономная немарковская система массового обслуживания и ее применение в задачах демографии: Дис. … канд. физ.-мат. наук: 05.13.18/Мария Геннадьевна Носова. — Томск, 2010. — 204 с.
- Гнеденко Б. В. Введение в теорию массового обслуживания. — 3–е изд., испр. и доп. — М.: КомКнига, 2005. — 397 с.
- Назаров А. А., Носова М. Г. Исследование математической модели демографических процессов в виде пятифазной системы массового обслуживания // Вестник Сибирского государственного аэрокосмического университета им. академика Решетнева. — 2010. — Том 1. — С. 53–58.
- Демографический ежегодник России 2015 // Федеральная служба государственной статистики (Росстат). URL: http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/publications/catalog/doc_1137674209312 (дата обращения: 19.10.2017).







