Наличие у жидкости релаксационных свойств определяет характер сопротивления при движении в пористой среде. Поскольку релаксирующая жидкость реагирует на изменение условий с некоторым запаздыванием, то в зависимости от скорости движения характер сопротивления будет изменяться. Когда течение достаточно медленное, соответственно медленно происходит деформация жидких частичек и жидкость успевает «реагировать» на эти изменения. С увеличением скорости движения время прохождения через сужения уменьшается, и жидкие частицы не успевают деформироваться, т. е. время релаксации уменьшается. Это приводит к увеличению сопротивления движения. В связи с вышесказанным определение времени релаксации, скорости фильтрации неравновесной жидкости и дебита имеет большое практическое значение, которое и рассматривается в данной статье.
Ключевые слова: жидкость, время релаксации, пористая среда, неравновесная жидкость
The presence of relaxation properties in the liquid determines the character of the resistance when moving in a porous medium. Since the relaxing liquid reacts to a change in conditions with some delay, depending on the speed of motion, the character of the resistance will change. When the flow is slow enough, the liquid particles deform slowly, and the liquid has time to «react» to these changes. As the speed of motion increases, the transit time through the constrictions decreases, and the liquid particles can’t deform, so the relaxation time decreases. This leads to an increase in drag. In connection with the foregoing, the determination of the relaxation time, the rate of filtration of the noequilibrium fluid and the production rate is of great practical importance, which is considered in this article.
Keywords: liquid, relaxation time, porous medium, noequilibrium fluid
При исследовании фильтрации неравновесных жидкостей необходимо учитывать, что вязкие силы, обусловливающие сопротивление, являются решающим фактором лишь в области малых скоростей фильтрации и заметно снижаются с ее увеличением. При этом преобладающую роль начинают играть уже упругие силы, так как жидкость не успевает релаксировать при переходе из одной поры и другую. Это приводит к увеличению эффективной вязкости, так как фактор сопротивления с увеличением скорости возрастает быстрее, чем скорость фильтрации. Доказано, что увеличение относительного сопротивления при увеличении скорости фильтрации пропорционально величине 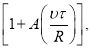 где
где ![]() – время релаксации; R — характерный масштаб изменения сечения; А — постоянная порядка десяти [1];
– время релаксации; R — характерный масштаб изменения сечения; А — постоянная порядка десяти [1]; ![]() — скорость фильтрации. Учитывая, что
— скорость фильтрации. Учитывая, что ![]() , увеличение сопротивления, выраженное через эффективную вязкость жидкости, можно представить в виде:
, увеличение сопротивления, выраженное через эффективную вязкость жидкости, можно представить в виде:
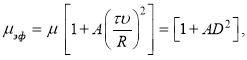 (1)
(1)
![]() где — вязкость жидкости; D — число Дебора,
где — вязкость жидкости; D — число Дебора, ![]() [2], равный отношению времени релаксации жидкости к характерному времени процесса.
[2], равный отношению времени релаксации жидкости к характерному времени процесса.
Таким образом, помимо числа Re течение характеризуется дополнительно новым параметром — числом Дебора. При малых числах Дебора ![]() влиянием релаксационных свойств можно пренебречь. При
влиянием релаксационных свойств можно пренебречь. При ![]() потери напора определяются не только вязкостью жидкости, но и параметром
потери напора определяются не только вязкостью жидкости, но и параметром ![]() . Для количественного описания этого закон фильтрации записывается в форме Дарси, но с переменной вязкостью (эффективной):
. Для количественного описания этого закон фильтрации записывается в форме Дарси, но с переменной вязкостью (эффективной):
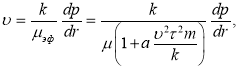 (2)
(2)
где а — постоянная одного порядка с А.
Последнее соотношение можно написать в виде:
![]() (3)
(3)
Откуда следует, что введение кубического слагаемого в аппроксимацию ![]() связано с необходимостью учета неравновесных свойств фильтрационного потока. Здесь
связано с необходимостью учета неравновесных свойств фильтрационного потока. Здесь ![]() Разделив обе части уравнения на а3, получаем:
Разделив обе части уравнения на а3, получаем:
![]() (4)
(4)
Пусть ![]() , тогда получаем:
, тогда получаем:
![]() . (5)
. (5)
Подставляя в уравнение (5) ![]() , получаем
, получаем
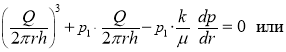
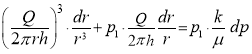 . (6)
. (6)
Интегрируя левую часть этого равенства от
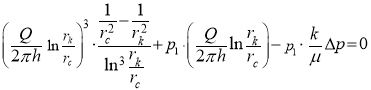 . (7)
. (7)
Сделав подстановку 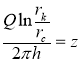 и разделив обе части равенства на
и разделив обе части равенства на 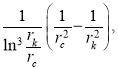 мы получаем уравнение в виде:
мы получаем уравнение в виде:
![]() , (8)
, (8)
где 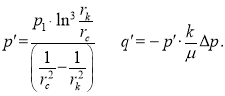
Используя формулу Кардано, находим решение этого уравнения:
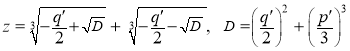 . (9)
. (9)
Преобразуя последнее выражение, имеем:
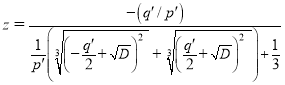 . (10)
. (10)
Учитывая, что 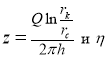 — знаменатель правой части выражения, получаем:
— знаменатель правой части выражения, получаем:
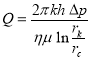 . (11)
. (11)
При малых скоростях
В наиболее общем виде его можно представить в виде ![]() Для определения
Для определения ![]() строится зависимость
строится зависимость ![]() при установившемся режиме фильтрации, где
при установившемся режиме фильтрации, где 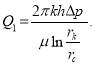 Полученная кривая аппроксимируется многочленом
Полученная кривая аппроксимируется многочленом ![]() Следует отметить
Следует отметить ![]() можно аппроксимировать в виде функции
можно аппроксимировать в виде функции ![]() .
.
Время релаксации можно определить по следующей формуле:
![]() (12)
(12)
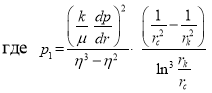 (13)
(13)
и ![]() (14)
(14)
Решая уравнения (13) и (14), получаем кубическое уравнение относительно ![]() в виде:
в виде:
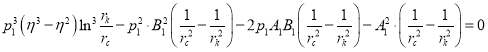 , (15)
, (15)
где ![]()
Решая это кубическое уравнение, находится зависимость ![]() где
где ![]()
Время релаксации при различных ![]() определяется по формуле
определяется по формуле
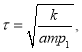 (16)
(16)
а скорость фильтрации при этом определяется с помощь формулы
![]() (17)
(17)
где ![]() определяется по формуле (14).
определяется по формуле (14).
Таким образом, проводя исследование методом установившихся отборов с помощью зависимости ![]() определяется
определяется ![]() и подстановкой в (15) находится зависимость для
и подстановкой в (15) находится зависимость для ![]() Далее, подставляя это значение в (16) и (17), определяются
Далее, подставляя это значение в (16) и (17), определяются ![]() и
и ![]()
Литература:
- А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. –Москва-Ижевск: Институт компьютерных исследований, 2005. –280 с.
- И. М. Аметов, Ю. Н. Байдуков, Л. М.Рузин, Ю. А.Спиридонов. — М.: Недра,1985. — 205 с.







