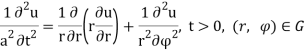Ключевые слова: функции, дифференциальные уравнения, Бессель, свойства функций
Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:
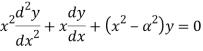
где 
— произвольное вещественное число (в общем случае комплексное), называемое порядком.
Функцию Бесселя индекса 
можно определить рядом:
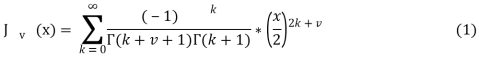
где 
— гамма–функция Эйлера.
Функция Бесселя представима в виде:
Где:
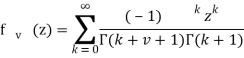(3)
По признаку Даламбера ряд сходится равномерно при всех 
, 
, где 
и 
— произвольные числа. Так как члены ряда представляют собой целые функции по переменной 
при фиксированном и по переменной при фиксированном , то 
является целой функцией при любом комплексном и целой функцией при любом фиксированном комплексном .
Все производные от функции как по переменной , так и по переменной ν могут вычисляться перестановкой суммирования и дифференцирования.
Рекуррентные соотношения для функций Бесселя
Для классических уравнений Бесселя с неотрицательным параметром 
и ограниченными в нуле решениями 
существуют рекуррентные соотношения вида:
и эти соотношения могут быть получены из общего вида классического уравнения Бесселя (1).
Также можно получить еще пару рекуррентных отношений, но для трех функций Бесселя:
Функции Бесселя первого рода
Функции Бесселя первого рода представляются в виде:
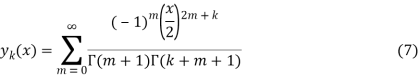
Формальная замена 
на 
дает функцию Бесселя первого рода отрицательного индекса 
:
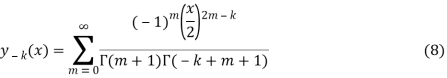
где 
—гамма-функция Эйлера.
Если функции (7) и (8) являются функциями целого индекса, 
, то их связывает линейное соотношение
то есть они линейно зависимы и не могут быть выбраны в качестве фундаментальной системы уравнения Бесселя.
Если же k не является целым числом, 
и 
линейно независимы.
Для того, чтобы найти общее решение уравнения (1), когда равно целому числу 
, необходимо найти второе, линейно-независимое от , частное решение. Для этого вводится новая функция, называемая функцией Бесселя второго рода.
Функции Бесселя второго рода
Функция Бесселя второго рода имеет вид:
Эта функция является линейной комбинацией частных решений и , следовательно, она тоже является решением уравнения (1).
Функция Вебера (10) является решением уравнения (1) и при 
.
Очевидно, и 
являются линейно независимыми, следовательно, при любом образуют фундаментальную систему решений уравнения (1). Тогда решение уравнения (1) можно представить в виде их линейной комбинации:
Свойства
Продифференцируем по 
ряд:
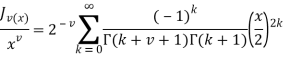
Справа получим:
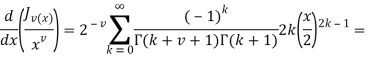
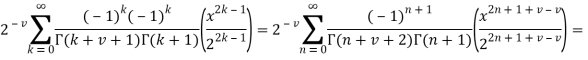
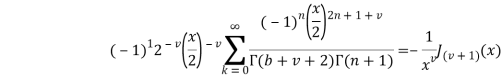
- Для функций Бесселя верны следующие формулы дифференцирования:
- Для функций Бесселя верны следующие формулы приведения:
- Свойство ортогональности функций Бесселя
Для любого k и любых корней 
функции верно равенство
-
Если
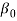-нуль функции 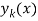, то
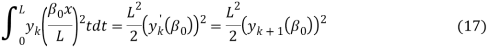
Пример краевой задачи
Требуется определить закон колебаний круглой мембраны. Математическая модель свободных колебаний круглой мембраны радиуса 
с закреплённым краем имеет вид следующей краевой задачи для определения поперечного смещения 
мембраны:
|
|
|
|
|
|
|
|
где
и 
— заданные смещения и скорость различных участков мембраны в начальный момент времени соответственно.
Решение этой задачи представляется в виде:
где 
и 
— функции Бесселя первого и второго рода
Применение:
Функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:
‒ Электромагнитные волны в цилиндрическом волноводе;
‒ Теплопроводность в цилиндрических объектах;
‒ Формы колебания тонкой круглой мембраны
‒ Распределение интенсивности света, дифрагированного на круглом отверстии.
‒ Скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси и др.
Литература:
- Зорич В. А. Математический анализ М.: ФАЗИС; Наука; Ч.I. — 1997, 568с.; Ч.II. — 1984, 640с.
- Зубов В. И. Функции Бесселя: Учебно-методическое пособие / Сост.: В. И. Зубов. — М.: МФТИ, 2007. — 51 с.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики: 2-e изд., стер. — М.: Наука, 1969. — 288 с.
