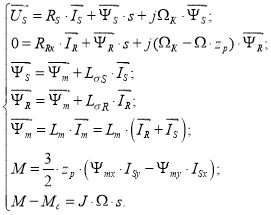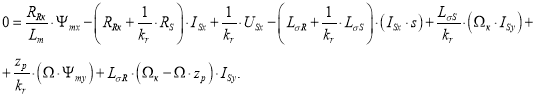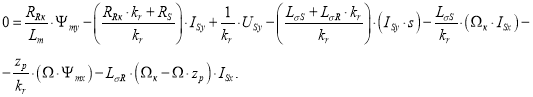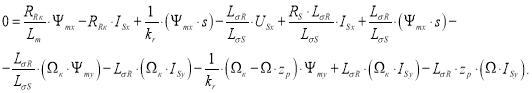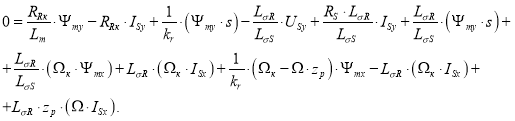Моделирование асинхронного двигателя с переменными Ψm – IS на выходе апериодических звеньев в системе абсолютных единиц в Simulink-Script



Моделирование асинхронного двигателя с переменными Ψ_m – I_S на выходе апериодических звеньев в системе абсолютных единиц в Simulink-Script

Емельянов Александр Александрович, доцент;

Бесклеткин Виктор Викторович, ассистент;

Пестеров Дмитрий Ильич, студент;

Одинцов Василий Олегович, студент;

Антоненко Илья Александрович, студент;

Коновалов Илья Дмитриевич, студент;

Бабкин Виталий Андреевич, студент

Российский государственный профессионально-педагогический университет (г. Екатеринбург)

В работе [1] дано математическое моделирование асинхронного двигателя с переменными ψ_m – i_s в системе относительных единиц. В этой работе приведена модель асинхронного двигателя с этими же переменными в системе абсолютных единиц.

Векторные уравнения асинхронного двигателя имеют следующий вид:

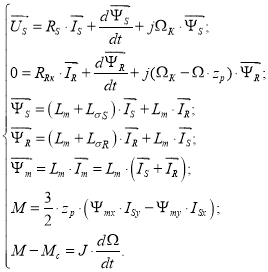
Обозначим токи, потокосцепления и индуктивности:

Переведем систему уравнений к изображениям :

	(1)
	(2)
	(3)
	(4)
	(5)
	(6)
	(7)

Схема замещения и векторная диаграмма в системе абсолютных единиц [3] даны на рис. 1 и 2.

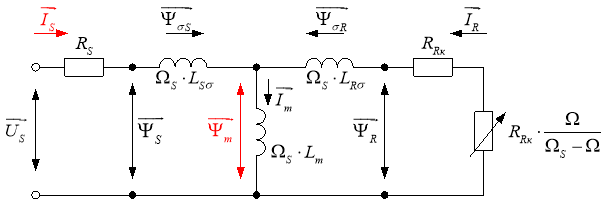
Рис. 1. Схема замещения асинхронного двигателя в системе абсолютных единиц

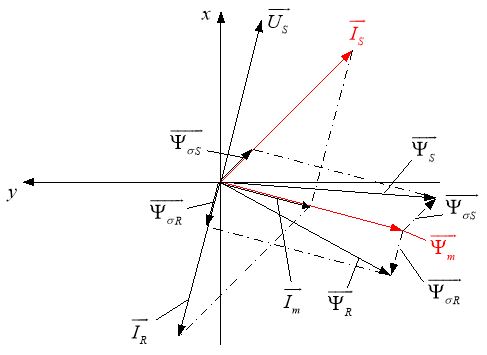
Рис. 2. Качественная картина расположения векторов в двигательном режиме в системе абсолютных единиц

Расписываем векторы через проекции:

Записываем уравнения (1), …, (4) по проекциям.

Уравнение (1):

По оси (+1):		(1’)
По оси (+j):		(1”)

Уравнение (2):

По оси (+1):		(2’)
По оси (+j):		(2”)

Уравнение (3):

По оси (+1):		(3’)
По оси (+j):		(3”)

Проекции потокосцепления Ψ_Sx и Ψ_Sy можно выразить и в следующей форме:

Уравнение (4):

По оси (+1):		(4’)
По оси (+j):		(4”)

Проекции потокосцепления Ψ_Rx и Ψ_Ry можно выразить и в следующей форме:

Уравнение (5):

По оси (+1):		(5’)
По оси (+j):		(5”)

Рассмотрим систему уравнений (1’), …, (5’) по оси (+1):

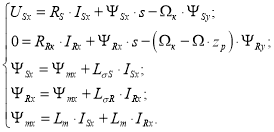
Из уравнения (5’) выразим IRx:

(6’)

Подставим I_Rx в уравнение (4’):

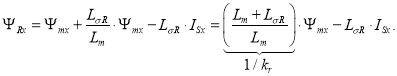
Обозначим :

(7’)

Рассмотрим систему уравнений (1”), …, (5”) по оси (+j):

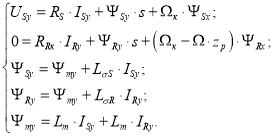
Из уравнения (5”) выразим IRy:

(6”)

Подставим I_Ry в уравнение (4”):

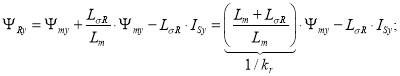
(7”)

Для уравнений (1’) и (2’) по оси (+1):

В первое уравнение подставим Ψ_Sx и Ψ_Sy из выражений (3’) и (3”):

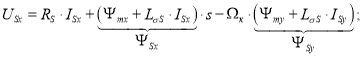
(8)

Из уравнения (8) выделим (Ψ_mx · s):

(8’)

Подставим в уравнение (2’) выражения I_Rx, Ψ_Rx и Ψ_Ry из уравнений (6’), (7’) и (7”):

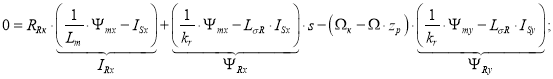
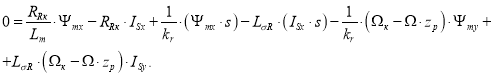
Затем внесем в полученное уравнение выражение (Ψ_mx · s) из (8’):

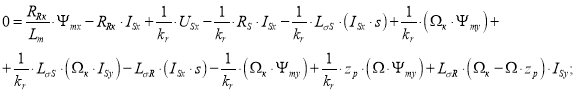
(9)

Перенесем в левую часть слагаемые с I_Sx:

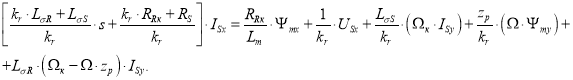
Обозначим:

Умножим обе части полученного уравнения на k_r:

В левой части вынесем за скобку R_S1:

Отсюда определим I_Sx:

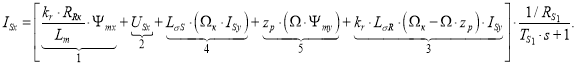
Структурная схема проекции статорного тока I_Sx на ось (+1) приведена на рис. 3.

Рис. 3. Структурная схема проекции статорного тока I_Sx на ось (+1)

Для уравнений (1”) и (2”) по оси (+j):

В первое уравнение подставим Ψ_Sy и Ψ_Sx из выражений (3”) и (3’):

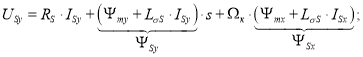
(10)

Из уравнения (10) выделим (Ψ_my · s):

(10’)

Подставим в уравнение (2”) выражения I_Ry, Ψ_Ry и Ψ_Rx из уравнений (6”), (7”) и (7’):

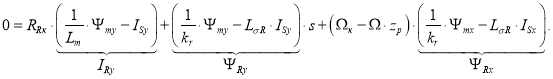
Внесем в полученное уравнение выражение (Ψ_my · s) из (10’):

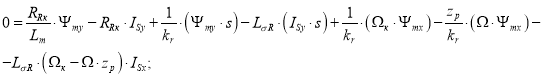
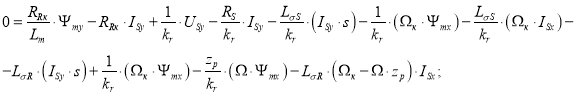
(11)

Перенесем в левую часть слагаемые с I_Sy и умножим обе части на k_r:

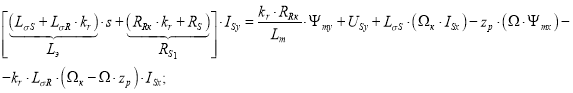
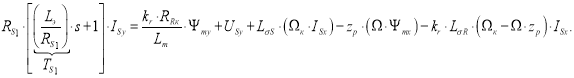
Отсюда ток I_Sy:

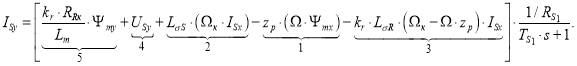
Структурная схема для реализации I_Sy приведена на рис. 4.

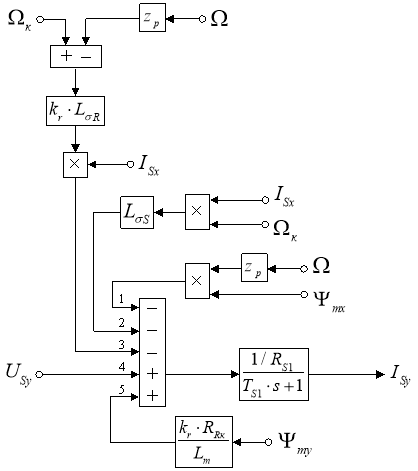
Рис. 4. Структурная схема для определения проекции статорного тока I_Sy на ось (+j)

Определение потокосцепления Ψ_mx.

Из уравнения (8) выделим (I_Sx · s):

(12)

Подставим в уравнение (2’) выражения I_Rx, Ψ_Rx, Ψ_Ry и (I_Sx · s) из уравнений (6’), (7’), (7”) и (12):

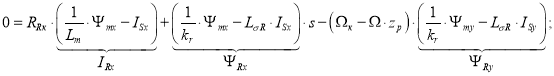
(13)

Перенесем в левую часть слагаемые с Ψ_mx:

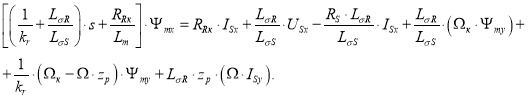
В левой части вынесем за скобки :

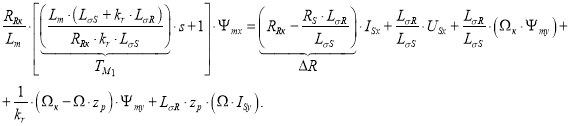
Обозначим:

и

Потокосцепление Ψ_mx определится следующим образом:

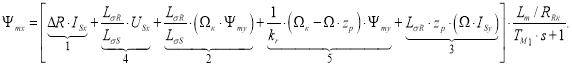
Структурная схема для определения потокосцепления Ψ_mx приведена на рис. 5.

Рис. 5. Структурная схема для определения потокосцепления Ψ_mx

Определение потокосцепления Ψ_my.

Из уравнения (10) выделим (I_Sy · s):

(14)

Подставим в уравнение (2”) выражения I_Ry, Ψ_Ry, Ψ_Rx и (I_Sy · s) из уравнений (6”), (7”), (7’) и (14):

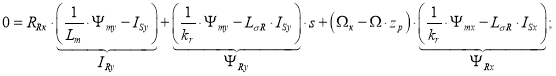
(15)

Перенесем в левую часть слагаемые с Ψ_my:

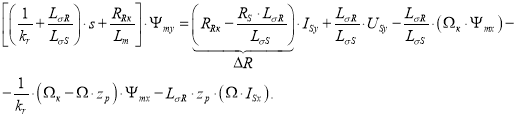
В левой части вынесем за скобки :

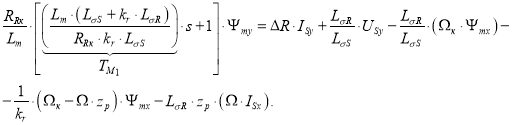
Определим потокосцепление Ψ_my:

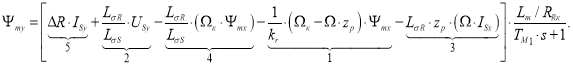
Структурная схема для определения потокосцепления Ψ_my приведена на рис. 6.

На рис. 7 представлена структурная схема для реализации уравнения электромагнитного момента (6):

Рис. 6. Структурная схема для определения потокосцепления Ψ_my

Рис. 7. Математическая модель определения электромагнитного момента M

Наконец, из уравнения движения (7) выразим механическую угловую скорость вращения вала двигателя (рис. 8):

Рис. 8. Математическая модель уравнения движения

Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными Ψ_m – I_S на выходе апериодических звеньев в системе абсолютных единиц приведена на рис. 9. Параметры асинхронного двигателя рассмотрены в работах [2] и [3].

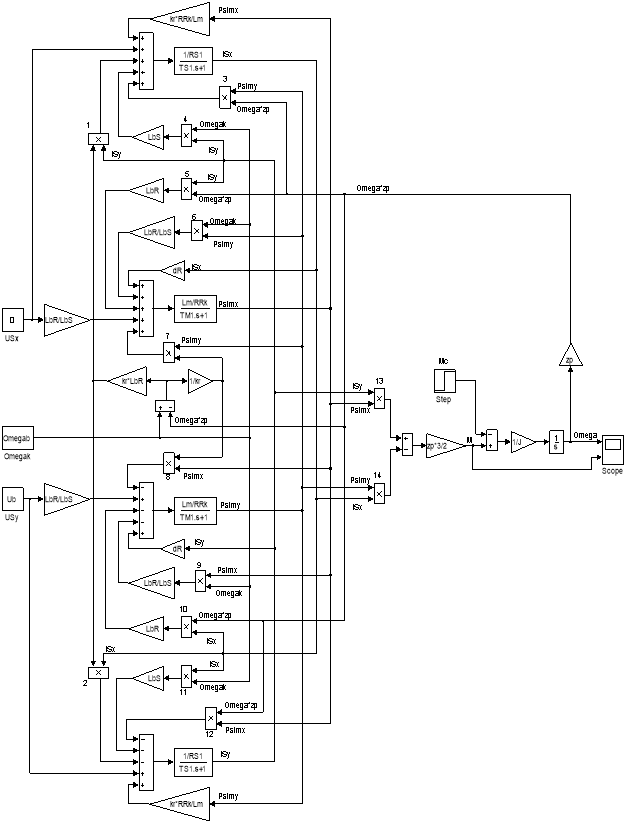
Рис. 9. Математическая модель асинхронного двигателя с переменными Ψ_m – I_S на выходе апериодических звеньев в системе абсолютных единиц

Расчет параметров производим в Script:

PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7; OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3; Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552;

J=28; Ub=sqrt(2)*UsN; Ib=sqrt(2)*IsN; OmegasN=2*pi*fN; Omegab=OmegasN; Zb=Ub/Ib; Psib=Ub/Omegab; Lb=Psib/Ib; rs=Rs/Zb; lbs=Xs/Zb; rr=Rr/Zb; lbr=Xr/Zb; lm=Xm/Zb; Lm=lm*Lb;

betaN=(Omega0N-OmegaN)/Omega0N; kr=lm/(lm+lbr); lbe=lbs+lbr+lbs*lbr*lm^(-1); roN=0.9962; rrk=roN*betaN; RRk=rrk*Zb; RS1=Rs+kr*RRk; LbS=lbs*Lb; LbR=lbr*Lb; Le=LbS+kr*LbR; TS1=Le/RS1; dR=RRk-Rs*LbR/LbS; TM1=Lm*(LbS+kr*LbR)/(RRk*kr*LbS);

Числовые значения параметров выводятся в окне Workspace (рис. 10).

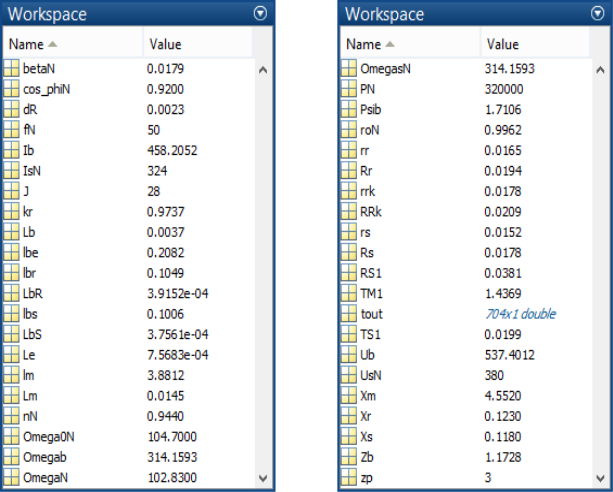
Рис. 10. Числовые значения параметров в окне Workspace

Результаты моделирования асинхронного двигателя представлены на рис. 11.

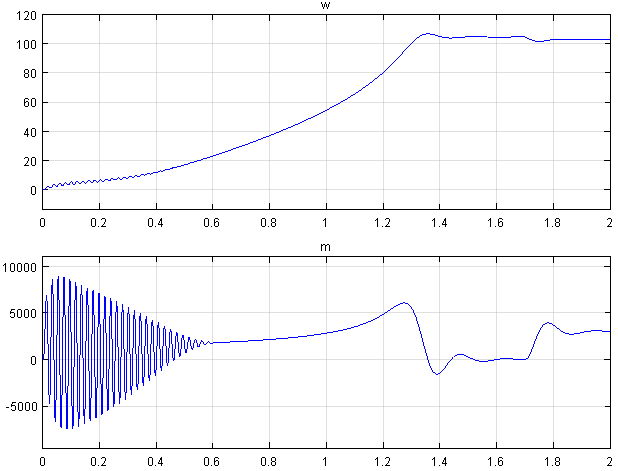
Рис. 11. Графики скорости и момента

Литература:

1. Емельянов А.А., Бесклеткин В.В., Антоненко И.А., Коновалов И.Д., Харин В.С., Ченцова Е.В., Федосеев П.В., Дугин П.И., Некрасова В.Н., Глух К.Ю., Солодова А.С. Математическая модель асинхронного двигателя с переменными ψ_m – i_s на выходе апериодических звеньев в Simulink-Script // Молодой ученый. - 2016. - №26. - С. 105-115.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
3. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.