В работе рассматриваются методы оценки точности численного решения CAE системы ФРУНД. ФРУНД — система инженерного анализа для моделирования систем твердых и упругих тел. Любая механическая система представляет собой совокупность деталей, тел, которые между собой связаны. Например, автомобиль — это механическая система, состоящая из колес, рамы, корпуса и т. д.
Всю систему физического мира можно описать при помощи дифференциальных уравнений. В системе ФРУНД по геометрическому изображению механической системы строятся дифференциальные уравнения, которые описывают его поведение, и после этого производится моделирование системы. Математическая модель механической системы позволяет с достаточной адекватностью судить о результатах моделирования. Если мы нарисуем автомобиль со всеми телами, связями и силами, действующими на каждое тело, зададим все необходимые параметры, то в результате моделирования этот автомобиль поедет.
В пакете ФРУНД проводится расчет собственных частот механических систем, но нет возможности оценить точность дискретного представления точного дифференциальных уравнений аналитической модели.
Для оценки точности предлагаем применять программу оценки точности использующей аналитические решения. Для решения задачи на собственные значения в аналитическом виде используется разложение решения по функциям Бесселя. Функции Бесселя используются для нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п.
В качестве примера расчета точности численного решения была выбрана круглая мембрана, т.к. круглых мембранных структуры используются во многих отраслях народного хозяйства. Для анализа механических свойств важно знать собственные частоты рассматриваемой мембраны. Это важно поскольку, в процессе работы может возникнуть эффект резонанса и привести к некорректной работе или даже разрушению мембранной структуры.
В ходе исследовательских работ была разработана программа для расчета собственных частот мембран круглой формы c нулевыми граничными условиями по границе, с помощью функции Бесселя. Собственная частота мембраны вычисляется по формуле (1):
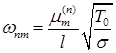 , (1)
, (1)
где 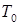 – натяжение,
– натяжение, 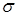 – поверхностная плотность мембраны,
– поверхностная плотность мембраны,  – радиус мембраны, m – номер корня уравнения
– радиус мембраны, m – номер корня уравнения 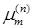 , в которое входит функция Бесселя первого рода:
, в которое входит функция Бесселя первого рода:
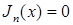 . (2)
. (2)
Для определения корней уравнения (2), была написана специальная программа. В работе рассматривается дискретная модель круглой мембраны, построенная методом конечных элементов. Собственные значения дискретной модели рассчитываются численным методом, путем решения задачи на собственные значения для соответствующих матриц инерции и жесткости. Собственные значения определялись с помощью модули, на вход которой подавались линеаризованные значения матриц инерции жесткости. Полученные численные значения собственных частот сравниваются с теоретическими значениями, полученными с использованием аналитических выражений. На основании такого сравнения делается заключение о величине шага разбиения сетки конечно-элементной модели.
Алгоритм был реализован, в качестве модуля расширения функциональности программного комплекса ФРУНД. Программный комплекс реализован на платформе WINDOWS, расчетные модули написаны на языках ФОРТРАН и С. Этот модуль планируется использовать для оценки точности численного решения, конечно-элементной модели программного комплекса ФРУНД.
На рисунке 1 показан расчет собственных частот в системе ФРУНД.
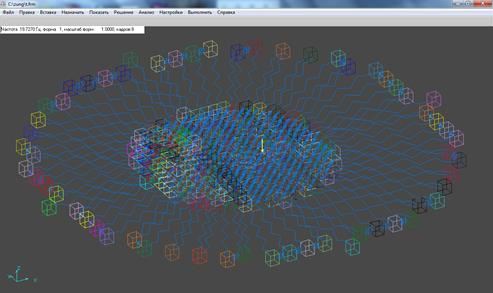
Рисунок 1 – Расчет собственных частот в ФРУНДе
Собственные частоты, полученные аналитическим путем, с помощью созданного модулю расширения функциональности показаны на рисунке 2.
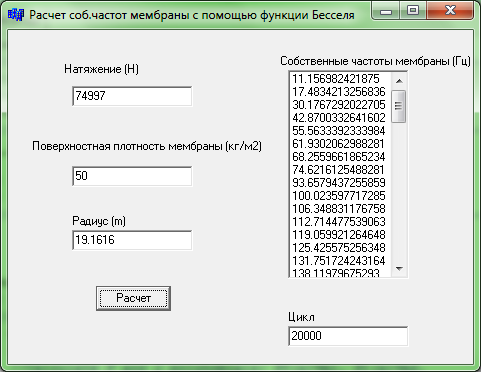
Рисунок 2 – Расчет собственных частот с помощью функции Бесселя
Результаты сравнения показаны на рисунке 3.
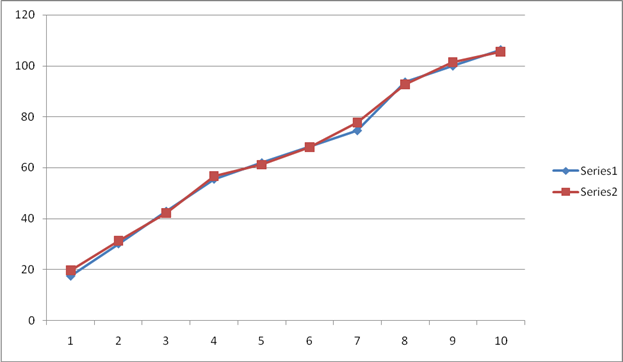 Рисунок 3 – Результат сравнения собственных частот
Рисунок 3 – Результат сравнения собственных частот
Выводы
1. Результаты показали точность между результатами модуля и пакета ФРУНД
2. Разработан способ оценки точности численных решений в CAE системах.
3. Реализован модуль оценки точности расчета собственных частот круглой мембраны.
Литература:
- Кошляков Н.С. Глинер Э.Б. Смирнов М.М. Уравнения в частных производных математической физики. М.: Высшая школа, 1970.
- Комплекс моделирования динамики систем твердых и упругих тел [Электронный ресурс]. - 2010. - Режим доступа: http://frund.vstu.ru
- Ефимов Г.Б., Погорелов Д.Ю. Универсальный механизм – пакет программ для моделирования динамики систем многих твердых тел. Препринт ИПМ им. М.В. Келдыша РАН № 77. – М., 1993.







