Вероятностные модели и программное обеспечение для организации тестового контроля знаний студентов

Современный этап развития образования в стране характеризуется проведением реформы, направленной на повышение эффективности и улучшения качества образования всех уровней. Как свидетельствует мировой опыт, успех подобных мероприятий обеспечивается лишь в том случае, если они подкреплены действенным реформированием системы проверки знаний. В связи с этим в последние годы были предприняты попытки создания новой, отличной от традиционной, системы педагогического контроля, основу которой составили педагогические измерительные материалы (ПИМ) – тестовые задания и тесты. Являясь частью педагогических новаций, тесты позволяют получить объективные оценки уровня знаний, умений, навыков и представлений, выявить пробелы в подготовке, проверить соответствие выпускников требованиям государственных образовательных стандартов. Иначе говоря, тесты представляют образовательный процесс в реальном свете. Их использование в сочетании с персональными ЭВМ и программно-педагогическими средствами позволяют оперативно и с высокой точностью оценить уровень подготовленности обучаемых. Задача преподавателя при такой организации контроля результатов учебного процесса заключается в разработке новых программно-педагогических средств, в организации процесса самостоятельного учения обучающихся [1]. Обучение должно начинаться с входного тестового контроля, сопровождаться самоконтролем и заканчиваться итоговым тестированием. Из сказанного ясно, что переход к новой системе проверки знаний связан с разработкой качественных ПИМ для всех уровней образования.

На сегодняшний день успешным можно считать решение этой задачи пока только для уровня среднего образования. За достаточно короткое время были созданы надежные ПИМы – для проверки знаний учащихся на этапах окончания школы и поступления в вуз практически по всем дисциплинам общеобразовательной программы, которые составили основу системы централизованного тестирования в России.

Иначе обстоит дело в профессиональном образовании. Количество специальных и учебных дисциплин здесь, в отличие от среднего образования, необозримо велико. Поэтому разработку необходимых комплексов тестов в профессиональном образовании только с помощью профессионалов-тестологов, как это было сделано для уровня среднего образования, выполнить невозможно. Во-первых, число квалифицированных тестологов в стране достаточно мало. Во-вторых, они не могут владеть материалом всего спектра учебных дисциплин, по которым должны быть созданы ПИМы, поскольку число дисциплин слишком велико. Выход из сложившейся ситуации: создать качественные ПИМы должны преподаватели, которые преподают эти дисциплины. Низкие темпы перехода к использованию тестовых технологий контроля знаний обучающихся профессиональных учебных заведений объясняется рядом причин. Во-первых, преподаватели-разработчики ПИМ в большинстве случаев не готовы к использованию современных методов математической статистики и методов теории педагогических измерений для проверки соответствия теста научно обоснованным критериям качества [1]. Без этого разработка надежного и качественного теста невозможна.

Во-вторых, современное положение в сфере тестового контроля осложняется отсутствием у подавляющего большинства преподавателей специальной подготовки по методике разработки и применения педагогических тестов. Остро ощущается недостаток, а порой и отсутствие методической литературы, где на доступном уровне излагается технология создания теста от этапа разработки предтестовых заданий до готового теста с известными характеристиками его качества.

В-третьих, неопытные разработчики, которых пока не мало, подвергают сомнению необходимость использования научно обоснованного подхода к разработке тестов [2]. Это связано с незнанием возможностей тестовых методов, непониманием их сильных и слабых сторон. Основные достоинства теста – получение объективных оценок уровня подготовленности обучающихся, их сопоставимость и возможность перепроверки – обеспечиваются не автоматически, а благодаря выполнению определенных требований к качеству заданий и всего теста в целом. Невыполнение этих требований приводит к тому, что тестовый контроль становится процедурой, не более определяющей представления о знании студентов, чем обычный экзамен.

Именно с необходимостью выработки у разработчиков ПИМ навыков научного обоснования качества тестовых материалов и связано использование в работе методов теории латентных переменных и методов математической статистики для обработки результатов тестирования.

В пользу широкого использования тестов в профессиональном образовании свидетельствуют и современные тенденции планирования учебной нагрузки в вузах, направленные на увеличение объема самостоятельной работы студентов. В большинстве вузов Российской Федерации до 60% объема часов дисциплины отводится на самостоятельное изучение и только 40% – на аудиторные занятия. При этом зачастую в расчет не принимается ни сложность материала конкретной дисциплины, ни значимость и влияние уровня ее освоения на профессиональную подготовку будущего специалиста. В этих условиях отказ от использования в учебном процессе тестов и тестовых технологий не позволит обеспечить надежный контроль структуры и уровня знаний студентов, а так же осуществлять их мониторинг. Кроме того, отсутствие тестов существенно затруднит как процесс проведения самообследования образовательных программ специальностей образовательных учреждений при их подготовке к аккредитации, так и проведение самой процедуры аккредитации существенно увеличит затраты на неё [3, 4].

Следует отметить, что интерес к тестам в профессиональном образовании в последнее время вырос. Но ситуация с их созданием в целом не улучшилась. Кажущаяся простота разработки и возросший спрос на тесты породили множество некачественных материалов, которые широко используются для контроля знаний студентов по отдельным дисциплинам, особенно в системе дистанционного обучения. Отмеченная ситуация находится в противоречии с мировой тенденцией повышения эффективности образования на основе применения тестов.

Важным шагом для повышения эффективности образования станет внедрение методов приемо-сдаточных испытаний в процесс тестового контроля. Далее рассматривается способ применения данной теории.

Пусть установлено некоторое нормативное значение показателя знаний R_н, а неизвестная фактическая величина имеет значение R, тогда процедуру контроля стремятся построить таким образом, чтобы с возможно более высокой вероятностью при R³R_н выставлялся зачет, а при R<R_н – незачет. Зависимость вероятности зачета L от значения показателя R называется оперативной характеристикой. При ограниченном объёме выборки N (числе вопросов, предлагаемых студенту по дидактической единице) она имеет вид, представленный на рисунке 1. Идеальная оперативная характеристика, т.е. характеристика, в которой  L®0 при R<R_н и  L®1 при R³R_н , может быть строго получена только при безграничном увеличении объёма выборки N®¥, практически, если тестируемый ответит на все вопросы, имеющиеся в базе данных по дидактической единице. 

Rн

R0

R1

R

L

 

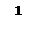
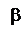
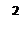
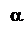
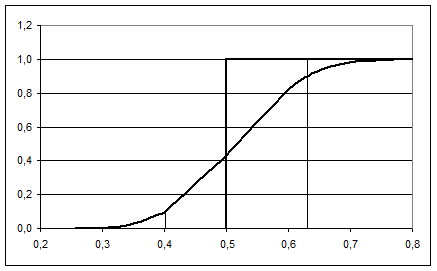
Рис.1. Оперативная характеристика: 1 – идеальная (при N®¥);

2 – реальная характеристика при N =30, a=b=0,1; R_н=0,5; R₀= 0,63; R₁= 0,4.

В процессе приёмо-сдаточных испытаний взаимодействуют две стороны экзаменуемый (студент) и экзаменатор (преподаватель), интересы которых в значительной мере противоположны. Студент заинтересован минимизировать вероятность aошибки первого рода, т.е. незачета при R³R_н, эту вероятность назовем риск студента. Преподаватель заинтересован минимизировать вероятность b ошибки второго рода – выставить зачет при R<R_н, эту вероятность назовем риск преподавателя. Как видно из рисунка 1, если в качестве условия незачета и условия зачета принять одно и то же значение R_н, то, так как в любой точке оперативной характеристики a+b=1, одновременно оба риска минимизировать невозможно.

Чтобы минимизировать оба риска возникает, необходимость установить два дополнительных уровня зачета-незачета: зачета R₁ и незачета R₀, которые на паритетных началах не существенно бы ущемляли интересы обеих сторон (R₁£R_н£R₀). Риск b  – это вероятность выставить зачет при R=R₁ или с ещё более низким уровнем знаний; риск a – это вероятность того, что и при R=R₀ или с ещё более высоким уровнем знаний студент получит незачет. Величины R₁, R₀, a и b устанавливаются организаторами тестирования.

Организация приёмо-сдаточных испытаний включает три этапа: планирование, проведение и анализ полученных результатов. Две точки  R₁, b  и  R₀, 1–a  полностью задают оперативную характеристику и позволяют спланировать испытания. В результате планирования определяется объём испытаний, а также правила зачета и незачета.

В существующей в настоящее время системе тестирования планирование испытаний производится чисто бюрократическим методом без учета характера процедуры тестирования, числа дидактических единиц, числа разрешенных попыток, всякий ли раз при повторном тестировании необходимо тестировать по всем дидактическим единицам и т.д. Существенно так же, что нигде не нормируются требования к уровню знаний.

  Исходными данными для планирования испытаний являются четыре величины R₀, R₁ (R₁£R_н£R₀) и a, b, которые должны нормироваться для каждого вида тестирования (текущий контроль, сессионный контроль, контроль остаточных знаний).  В результате планирования должны быть определены объём испытаний N и норматив зачета r_з или незачета r_н (r_з=r_н+1).  Для этого решается система уравнений 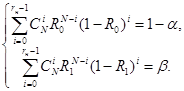(1):

                                                                                    (1)

Результатом испытаний является число правильных ответов r_п или число ошибочных ответов r_о (r_п+r_о=N). При r_п ≥ r_з студент получает зачет, иначе незачет [5].

Из условий паритета интересов целесообразно принять a=b, а из соображений компромисса, чтобы были не слишком велики и риски, и объем испытаний, целесообразно принять a=b=0,1. Так как величины N и r_н дискретные, система уравнений (1) имеет решение не при любых значениях  R₀ и R₁. Поэтому задача планирования испытаний решается иначе. Задаются значения N, r_н и из уравнений (1) определяются величины R₀ и R₁.Затем рассчитываются средние значения уровня зачета-незачета R_ср=(R₀+R₁)/2  и  относительное  расхождение  между  величинами  δ=(R₀–R₁)/R_ср. По полученным данным выбираются наиболее подходящие значения R_ср и δ, затем по ним определяются N и r_н и затем, решая систему уравнений (1) находятся искомые значения  R₀ иR₁.

Следует иметь ввиду, что вероятности правильного ответа на вопрос теста R_н, R₀, R₁, R_ср, это еще не те величины, которые подлежат нормированию. Как было показано, вероятности правильного ответа зависят не только от уровня знаний студента z_н, который необходимо нормировать, но и от характера вопросов, от числа ДЕ, числа разрешенных пересдач. Задав значение z_н, по приведенным формулам можно рассчитать нормируемую величину R_н  [6].

Зависимость вероятности нормируемого правильного ответа студента по одной ДЕ р_н от уровня его знаний z_н рассчитывается по приближенной формуле

p_н= z_н ×р_со + (1– z_н)×( р₁×v₁ + р₂×v₂ + р₃×v₃),                                                                               (2)

где      р_со – вероятность правильного ответа с учетом возможной нечеткости вопроса и случайных ошибок студентов, р_2i  » 0,9;

р₁ – вероятность правильного ответа наугад на вопрос первого типа, 

;

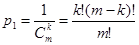р₂ – вероятность правильного ответа наугад на вопрос второго типа,

р₂ = 1/ m ;

р₃ – вероятность правильного ответа наугад на вопрос третьего типа,

р₃= 1/ m!;

m – число ответов;

k – число правильных ответов;

v₁ – доля вопросов первого типа;

v₂ – доля вопросов второго типа;

v₃ – доля вопросов третьего типа;

v₁ + v₂ + v₃ = 1.

Требование знаний студентов по всем ДЕ целесообразно принять одинаковыми, тогда нормируемая вероятность успешной сдачи зачета по дисциплине p_н, по которой выделено М дидактических единиц, при условии однократного тестирования

Р_н=p_н^М .                                                                                                                                  (3)

Окончательно, нормируемая вероятность при k разрешенных попытках сдачи равна [7]

R_н =1– (1– Р_н)^k .                                                                                                                      (4)

Руководствуясь описанным выше можно определить, что количество задач, которые возможно решать в области тестового контроля на данный момент очень велико. Многие аспекты организации и проведения тестового контроля нуждаются в оптимизации и улучшении.

Для более подробного рассмотрения был выбран вопрос прямого расчета количества требуемых правильных ответов по каждой дидактической единице в зависимости от требуемого уровня знаний студентов и количества дидактических единиц.

Программные решения были разработаны с помощью универсального языка программирования Borland Delphi 7.0. Это позволило создать интуитивно понятный интерфейс и простой способ использования приложений. Все внутрипрограммные расчеты выполнены с опорой на реальную статистику по тестовому контролю знаний студентов. Так вероятность угадывания выбрана равной 0,22, как среднее значение по всем видам вопросов в базе системы тестирования РГУПС, а так же руководствуясь их процентным соотношением. При этом программа допускает изменение этой вероятности.

Далее более подробно рассмотрено предложенное программное решение, описаны методы работы с ним, способы интерпретации результатов, представлены графики, упрощающие понимание расчетов и иллюстрирующие работу программы.

Данный программный продукт был разработан с целью математического обоснования выбора проходного балла для тестов в зависимости от количества дидактических единиц и требуемого от тестируемого необходимого минимального уровня знаний. Интерфейс приложения представлен на рисунке 2:

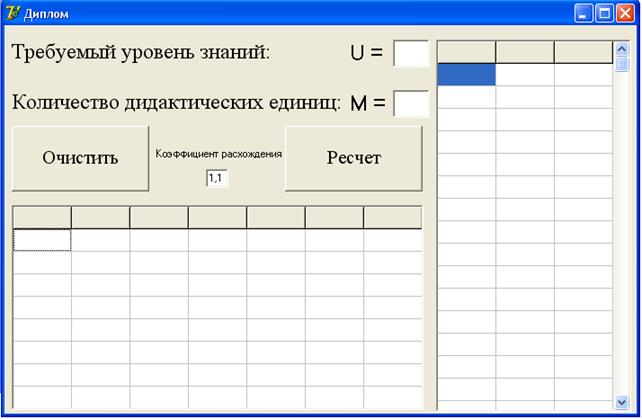
Рис.2. Интерфейс программы определения уровня зачета в зависимости от требуемого уровня знаний

Расчет проводится с использованием формулы (2) и системы уравнений (1), но с учетом количества дидактических единиц и количества вопросов в них. Это входные данные. Так же  можно изменить установленный коэффициент расхождения. Он был определен эмпирически и при запуске программы установлен в значение 1,1. Вывод результатов сведен в таблицу под полями для ввода данных, столбцы таблицы, начиная с крайнего левого: требуемый минимальный уровень знаний тестируемых; количество дидактических единиц; верхняя граница расчетного проходного балла; нижняя граница расчетного проходного балла; вероятность ошибки первого рода; вероятность ошибки второго рода; минимально необходимое количество вопросов, на которые должен ответить тестируемый для соответствия требуемому уровню знаний. Кроме этих данных, накапливаемых в таблице от расчета к расчету, для большей информативности вычислений представлена таблица справа, на которой отображаются вероятности ошибок первого и второго рода для каждого вопроса в конкретной дидактической единице. Эти данные не накапливаются, а заменяются новыми при пересчете с новыми входными данными. В этом приложении так же возможно очищать таблицу для расчетов с новыми данными.

Полученные результаты можно представить несколькими способами, например, в таком виде (таблица 1):

Таблица 1. Зависимость проходного балла от количества дидактических единиц и уровня знаний

		Количество ДЕ
		1	2	3	4	5	6
Требуемый уровень знаний	0,3	31	17	13	10	9	8
	0,4	35	20	14	11	10	8
	0,5	39	22	15	12	10	9
	0,6	44	24	17	13	11	9

 

При данных проходных баллах значения риска преподавателя (α) будет таким (таблица 2):

Таблица 2. Значения риска преподавателя для полученных проходных баллов

		Количество ДЕ
		1	2	3	4	5	6
Требуемый уровень знаний	0,3	0,078	0,098	0,044	0,073	0,028	0,020
	0,4	0,090	0,048	0,068	0,075	0,018	0,068
	0,5	0,099	0,049	0,095	0,069	0,065	0,024
	0,6	0,061	0,044	0,034	0,053	0,027	0,076

 

Риски студента (β) при тех же значениях проходных баллов будут следующими (таблица 3):

Таблица 3. Значения риска студента для полученных проходных баллов

		Количество ДЕ
		1	2	3	4	5	6
Требуемый уровень знаний	0,3	0,958	0,939	0,972	0,950	0,981	0,986
	0,4	0,959	0,976	0,961	0,954	0,990	0,955
	0,5	0,963	0,980	0,951	0,963	0,963	0,986
	0,6	0,984	0,985	0,986	0,975	0,987	0,959

           

По-другому результаты можно трактовать, представив их диаграммой (рис. 3):

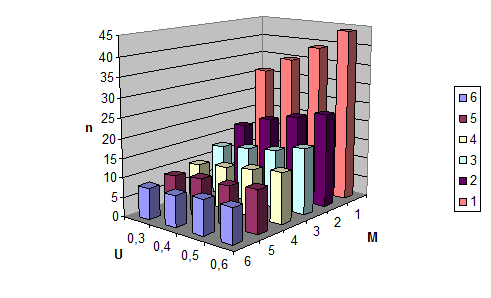
Рис.3. Графическое представление зависимости проходного балла от требуемого уровня знаний и числа дидактических единиц

Можно заметить, что полученные результаты отличаются от тех, что используются в настоящий момент в системе тестирования и решения о выставлении зачета по фиксированному проходному баллу в 30 или 50% не совсем состоятельны. Кроме того, стоит обратить внимание на тенденцию при увеличении числа дидактических единиц – при любом требуемом уровне знаний необходимое для получения зачета число правильных ответов приближается к общему числу вопросов в каждой ДЕ. При неизменном общем числе вопросов увеличение числа ДЕ не имеет смысла, так как такой подход не снижает риск преподавателя, а только повышает риск студента, оставляя ему меньше шансов на удачное прохождение тестирования, даже при обладании необходимыми для этого знаниями. По существу такой подход может вынуждать студентов и преподавателей фальсифицировать результаты тестирования.

 

Литература:

1.      Аванесов, В.С. Современные методы обучения и контроля знаний: Учебное пособие для преподавателей вузов, техникумов и училищ, учителей школ, гимназий и лицеев, для студентов и аспирантов педагогических вузов / В.С. Аванесов. – М.: Кидди (Kiddy), 1998. – 103 с.

2.      Челышкова, М.Б. Теория и практика конструирования педагогических тестов: Учебное пособие / М.Б. Челышкова – М.: Логос, 2002. – 432 c.

3.      Автоматизированные  тестовые технологии контроля знаний студентов – основа внутривузовских систем менеджмента качества образования / А.Г. Сапронов, И.Н. Елисеев, И.М. Мальцев, И.И. Елисеев // Вопросы тестирования в образовании. – 2004. – № 12. – С. 53–62.

4.      Сапронов А.Г. Роль тестирования в условиях функционирования систем менеджмента качества образования в Южно-Российском государственном университете экономики и сервиса (ЮРГУЭС) / А.Г. Сапронов, И.Н. Елисеев, И.И. Елисеев // Вопросы тестирования в образовании. – 2005. –     № 15(3). – С. 112–114.

5.      Нейман, Ю.М. Введение в теорию моделирования и параметризации педагогических тестов / Ю.М. Нейман, В.А. Хлебников. – М.: Прометей, 2000. – 169 с.

6. Линденбаум, М.Д. Надежность информационных систем / М.Д. Линденбаум, Е.М. Ульяницкий: Учебник для вузов ж.-д. транспорта. – М.: ГОУ «Учебно-методический центр по образованию на железнодорожном транспорте», 2007. – 318 с.
7. Колесников, В.И.  Математическое обоснование оценки уровня подготовки студентов в форме компьютерного тестирования / В.И. Колесников, В.М. Гуськова, М.Д. Линденбаум, А.А. Порческо, Р.И. Островский // Вестник Ростовского государственного университета путей сообщения. – 2009. – № 3. – С. 135-141.