Основным мотивом к выбору темы явилось изучение причинно–следственных отношений в сложной системе «хаос – порядок» и тем более поиск их эвентуальных связей с "золотым" сечением, которое лежит в основе фибоначчиевой модели, представляют большой познавательный интерес. В этом аспекте заслуживает внимания, например, исследование ассиметричной симметрии между хаосом и порядком в круговороте энергии по правилу гармонической пропорции.
Цель данной работы имеет два аспекта. Первый - логически обосновать важную роль числа Фибоначчи в математике и различных областях человеческой деятельности. Второй аспект- применение кода Фибоначчи в динамике фрактальных систем.
Фракталом же называется структура, состоящая из частей, подобных целому. Согласно другому определению, фрактал представляет собой геометрический объект с дробной (нецелой) размерностью. Кроме того, фрактал всегда возникает в результате бесконечной последовательности однотипных геометрических операций по его построению, т.е. является следствием предельного перехода, что роднит его с золотым сечением, которое тоже представляет собой предел бесконечного числового ряда, составленного из отношений соседних чисел Фибоначчи. Наконец, размерность фрактала, как правило, является иррациональным числом (как и золотое сечение) [1].
Размерность снежинки Коха и губки Менгера выражает через золотое сечение:
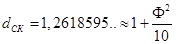
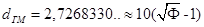
Мы видели, что размерности многих классических фракталов с той или иной степенью точности могут быть выражены через золотое сечение. Таким образом, можно высказать осторожное предположение о тесной взаимосвязи размерности большинства фрактальных множеств и золотого сечения.
В работе было показано, что для идеальной нелинейной динамической системы 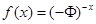 аддитивная рекурсия ее двух предшествующих состояний
аддитивная рекурсия ее двух предшествующих состояний 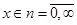
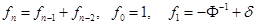
при сколь угодно малом значении 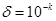 за конечное число шагов
за конечное число шагов 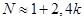 выводит систему из равновесия и приводит к бифуркации (рис. 1).
выводит систему из равновесия и приводит к бифуркации (рис. 1).
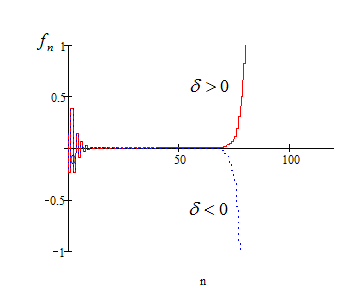
Рис. 1. Бифуркация (расслоение) решений нелинейной динамической модели:
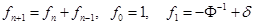
Изложенное позволяет высказать гипотезу, что такая система является прообразом образования космоса или кодом Вселенной, в основе которого лежит аддитивная рекурсия с "золотой" пропорцией [2].
В этой работе были исследованы динамика Ф-отображения и уникальные инвариантные плотность и функция распределения Ф-отображения.
Первым задачу об исследовании отображения [3]:
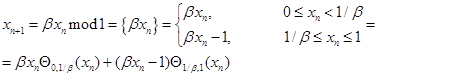 (1)
(1)
с произвольным вещественным параметром 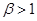 (далее мы ограничимся случаем
(далее мы ограничимся случаем 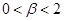 ) поставил, видимо, А. Реньи. Здесь при записи отображения введена индикаторная функция:
) поставил, видимо, А. Реньи. Здесь при записи отображения введена индикаторная функция:
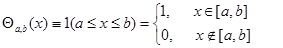
Внутри указанного промежутка она равна единице, а за его пределами равна нулю; вариация обозначений для индикаторной функции удобна при проведении операций с этой функцией.
В. А. Рохлин доказал, что подобное отображение является точным эндоморфизмом, т. е. перемешивающим эргодическим отображением. Это очень важный общий результат, стимулирующий детальное исследование (1). Интересно выяснить, что же происходит с характеристиками отображения (инвариантной плотностью, собственными функциями и собственными числами оператора Перрона-Фробениуса, автокорреляционной функцией орбит отображения и т. д.) при изменении параметра 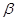 .
.
В качестве отображения с конкретным значением параметра 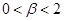 Мори (вслед за Реньи и Рохлиным) рассмотрел хаотическое отображение (оно так и было названо — «
Мори (вслед за Реньи и Рохлиным) рассмотрел хаотическое отображение (оно так и было названо — «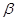 -отображение»), параметр которого равен одному из иррациональных чисел Фидия,
-отображение»), параметр которого равен одному из иррациональных чисел Фидия,
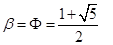 (2)
(2)
причем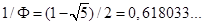 . Инвариантная плотность является кусочно-постоянной (двухступенчатой) функцией:
. Инвариантная плотность является кусочно-постоянной (двухступенчатой) функцией:
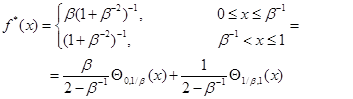 (3)
(3)
Соответствующая кусочно-линейная функция распределения имеет терпит излом в точке 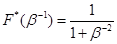 :
:
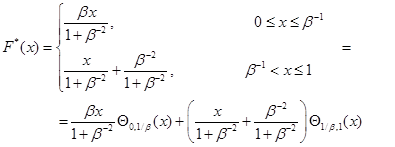 (4)
(4)
Вид отображения (1) с коэффициентом (2) — Ф - отображения — показан на рис. 2. Графики дифференциального и интегрального законов распределения (3) и (4) представлены на рис. 3.
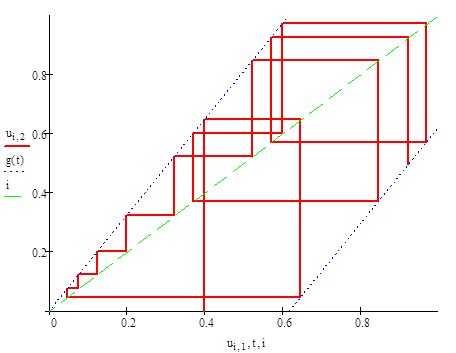
Рис. 2. Отображение Реньи с коэффициентом, равным золотому сечению (Ф-отображение)
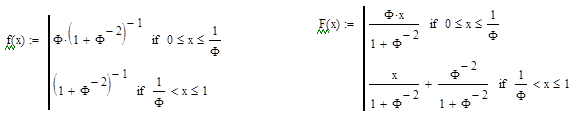
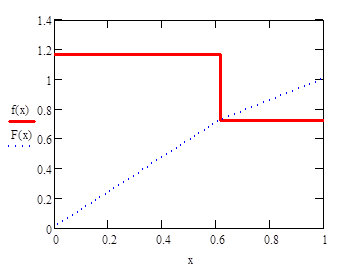
Рис. 3. Инвариантные плотность (сплошные линии) и функция распределения Ф - отображения (точка разрыва — 1/Ф).
В работе рассмотрено и обосновано появление золотой пропорции в динамических фракталах, связанное с переходом системы в устойчивое состояние и золотая пропорция – это код устойчивости фрактальной структуры.
В работе рассмотрены бифуркация в нелинейной динамической модели на основе золотого сечения. Показана чувствительность рассматриваемой динамической системы к малому изменению начальных условий и продемонстрирован на компьютерной модели процесс бифуркации нелинейной динамической модели. Рассмотрены уникальность стохастических характеристик Ф – отображения (Реньи) в виде плотности в форме двух ступенек.
Литература:
- Шипицын Е.В., Попков В.В. “Двойственность и золотое сечение в теории фракталов и хаоса”. // Вестник Международного института А. Богданова. 2001. № (6).
- С.Л. Василенко, Бифуркации в нелинейной динамической модели на основе «золотого» сечения // «Академия Тринитаризма». М., Эл № 77-6567, публ.15232, 14.04.2009.
- Аникин В.М., Голубенцев А.Ф. Аналитические модели детерминированного хаоса. – М.: Физматлит, 2007. - 328 с. – ISBN 978-5-9221-0879-9.







