В работе предлагается метод, по которому можно более простым способом решать гидродинамические задачи, связанные с фильтрацией аномальной нефти в пласте и вообще при фильтрации любого флюида с учетом начального градиента.
Ключевые слова: начальный градиент, аномальная нефть, фильтрация, флюид, закон Дарси
The paper proposes a method by which it is possible to solve the hydrodynamic problems associated with the filtration of anomalous oil in a reservoir in a simpler way and in general when filtering any fluid taking into account the initial gradient
Keywords: initial gradient, anomalous oil, filtration, fluid, Darcy law
Рассмотрим вязкопластичную фильтрацию нефти в пористой среде. В этом случае [1] скорость радиальной фильтрации выражается в следующем виде:
![]() , (1)
, (1)
![]() (2)
(2)
Как известно, дебит при этом определяется по формуле:
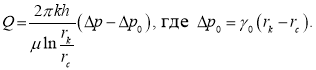 (3)
(3)
А теперь сделаем попытку получить эту же формулу, представляя, что фильтрация происходит как бы по закону Дарси. Однако для учета влияния начального градиента изменим пределы интегрирования. Учитывая, что для фильтрации жидкости в пористой среде с начальным градиентом депрессия тратится не только на преодоление давления на призабойной зоне рс, но и на преодоление начального градиента призабойной зоны. Это логично, так как основное снижение давления происходит в призабойной зоне.
Как известно, без учета начального градиента
![]() ,
,
откуда ![]() . (4)
. (4)
Интегрируя левую часть от![]() , а правую часть от
, а правую часть от ![]() , получаем:
, получаем:
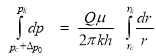 (5)
(5)
или 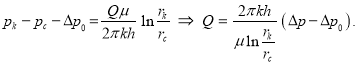
Как видно, последняя формула полностью совпадает с формулой (3).
А теперь рассмотрим влияние начального градиента на фильтрацию газа в пористой среде. Будем интегрировать непосредственно
считая фильтрацию плоскорадиальной.
Выразим скорость фильтрации через приведенный объемный дебит ![]() используя формулу для плотности
используя формулу для плотности ![]() и соотношения
и соотношения
![]() (7)
(7)
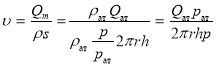 . (8)
. (8)
Подставляя выражение (8) в (6), получаем:
![]() (9)
(9)
Затем разделим переменные ![]() и, проинтегрируя от забоя
и, проинтегрируя от забоя ![]() до контура пласта
до контура пласта ![]() получаем:
получаем:
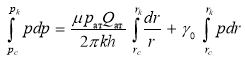 , (10)
, (10)
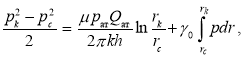 (11)
(11)
откуда 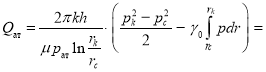
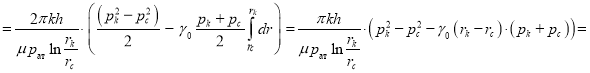
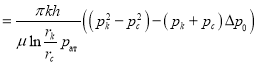 . (12)
. (12)
Здесь для возможности вычисления второго интеграла приведен способ осреднения ![]()
А теперь покажем, что
![]() (13)
(13)
Сначала докажем левую часть неравенства:
![]()
Действительно, так как ![]() то
то ![]()
![]()
![]()
Так как ![]() то
то![]()
Докажем правую часть неравенства:
![]() ,
,
![]()
Подставляя ![]() имеем:
имеем:
![]() ,
,
![]()
Учитывая доказанное неравенство (13), можно для фильтрации газа в пористой среде с учетом начального градиента написать следующее неравенство:
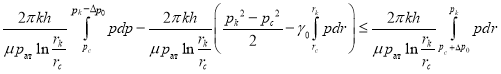 ,
,
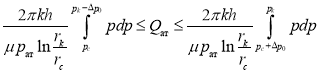 (14)
(14)
![]() .
.
В таблице 1 приведены результаты расчетов для каждого из этих дебитов. Как видно из табл. 1, они почти полностью совпадают. Разность между ними находится в пределах 0,1 %. Последнее показывает, что при фильтрации газа в пористой среде с учетом начального градиента также можно использовать закон Дарси, учитывая влияние начального градиента, задавая условие на пределах интегрирования.
А теперь попытаемся доказать это утверждение в наиболее общем виде. Анализ существующих в литературе работ показал, что для прогнозирования дебита лучше всего подходит методика, разработанная в [2,3,4,5], так как в ней наиболее полно учитываются все вышеперечисленные факторы. Согласно этой методике уравнение стационарного притока флюида к скважине представляется в виде:
![]() ,
,
где 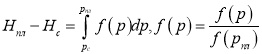 . (15)
. (15)
Здесь для реального газа и газоконденсатной смеси в условиях ![]()
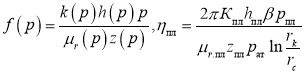 ; (16)
; (16)
для газоконденсатной смеси в условиях ![]()
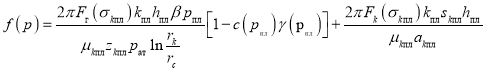 . (17)
. (17)
Здесь ![]() – соответственно текущее давление и насыщенность пласта конденсатом в любой точке пласта;
– соответственно текущее давление и насыщенность пласта конденсатом в любой точке пласта; ![]() — дебит скважины;
— дебит скважины; ![]() — коэффициент, характеризующий нарушение линейного закона фильтрации;
— коэффициент, характеризующий нарушение линейного закона фильтрации; ![]() – коэффициент продуктивности скважин;
– коэффициент продуктивности скважин; ![]() – соответственно абсолютная, фазовая проницаемости и действующая толщина пласта;
– соответственно абсолютная, фазовая проницаемости и действующая толщина пласта; ![]() — вязкость и сжимаемость газа;
— вязкость и сжимаемость газа; ![]() – соответственно содержание конденсата в газовой среде и отношение удельных весов конденсата в жидкой и газовой фазах в нормальных условиях;
– соответственно содержание конденсата в газовой среде и отношение удельных весов конденсата в жидкой и газовой фазах в нормальных условиях;![]() — растворимость газа в конденсате,
— растворимость газа в конденсате,![]() — объемный коэффициент конденсата;
— объемный коэффициент конденсата; ![]() — температурная поправка;
— температурная поправка; ![]() — давление начала конденсации газоконденсатной смеси.
— давление начала конденсации газоконденсатной смеси.
Индексом «пл» обозначены величины соответствующих параметров при пластовых давлениях ![]() .
.
Для однофазной нефти
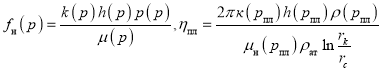 . (18)
. (18)
Для жидкой фазы газированной нефти
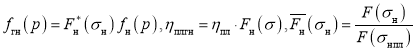 . (19)
. (19)
Здесь ![]() и
и ![]() –соответственно текущее давление и насыщенность коллектора флюидом в произвольной точке пласта;
–соответственно текущее давление и насыщенность коллектора флюидом в произвольной точке пласта; ![]() — коэффициент продуктивности скважины,
— коэффициент продуктивности скважины, ![]() — соответственно абсолютная и фазовая проницаемости и действующая толщина пласта;
— соответственно абсолютная и фазовая проницаемости и действующая толщина пласта; ![]() — вязкость и плотность флюида.
— вязкость и плотность флюида.
Для вывода основной расчетной формулы для всех этих разных случаев с учетом влияния изменения физических свойств флюида и коллектора примем, что зависимость комплекса параметров от депрессии можно в наиболее общем случае аппроксимировать многочленом степени n, т. е.
![]() . (20)
. (20)
С целью вывода уравнения притока с начальным градиентом давления формулу
![]() (21)
(21)
преобразуем в следующий вид:
![]() .
.
Таблица 1
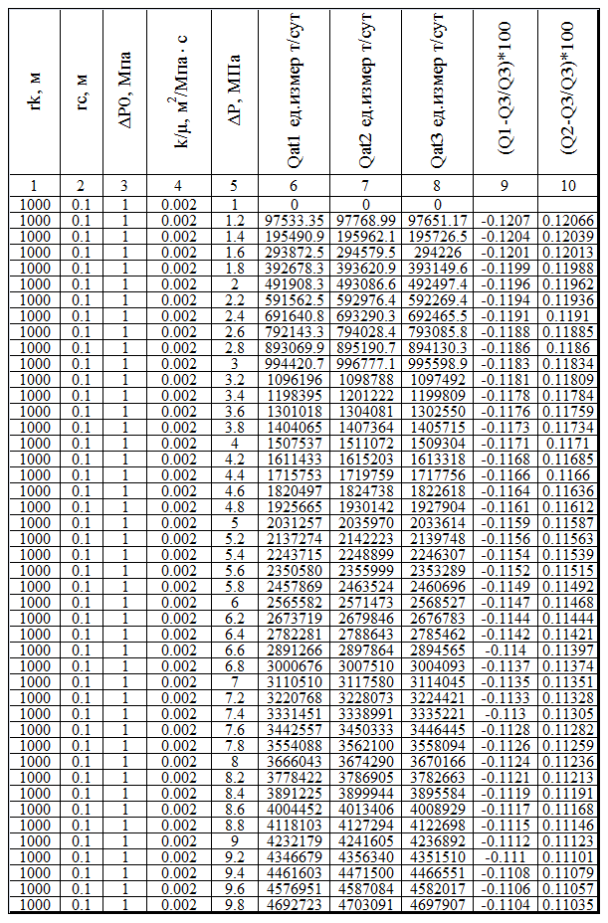
Здесь
![]() , (22)
, (22)
то, проводя аналогичные преобразования, получаем выражение [4]:
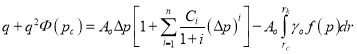 . (23)
. (23)
Здесь ![]() — коэффициент макрошероховатости, характеризующий структуру порового пространства;
— коэффициент макрошероховатости, характеризующий структуру порового пространства; ![]() плотность;
плотность; ![]() коэффициент, характеризующий двучленный закон фильтрации;
коэффициент, характеризующий двучленный закон фильтрации; ![]() начальное значение коэффициента продуктивности. В работе [4, 5] показано, что формула (23) после несложных преобразований принимает вид:
начальное значение коэффициента продуктивности. В работе [4, 5] показано, что формула (23) после несложных преобразований принимает вид:
![]() . (24)
. (24)
При ![]() получаем:
получаем:
![]() . (25)
. (25)
Последние две формулы можно получить не учитывая в формулах ![]() то есть используя двучленный закон фильтрации и учитывая влияние начального градиента, задавая условие для давлении в пределах интегрирования:
то есть используя двучленный закон фильтрации и учитывая влияние начального градиента, задавая условие для давлении в пределах интегрирования:
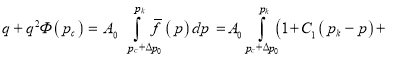
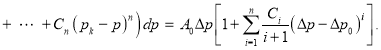
Таким образом,
![]() (26)
(26)
или при ![]()
![]() (27)
(27)
Здесь ![]()
Как видно, формулы (26) и (27) полностью совпадают с (24) и (25), что и следовало доказать.
Литература:
- Ф. Х. Мирзаджанзаде, А. Г. Ковалев, Ю. В. Зайцев. Особенности эксплуатации месторождений аномальных нефтей. –М.: Недра, 1972. — С.200.
- Абасов М. Т., Азимов Э. Х. К методике обработки индикаторных линий скважин // Докл. АН Аз.ССР. –1987. –Т.43. –№ 4. –С.33–37.
- Методика интерпретации индикаторных линий газовых и газоконденсатных скважин /Э. Х. Азимов, В. Н. Аллахвердиев, Л. М. Билаллы, И. Р. Гасанов // Азерб.нефт.хоз-во. –1987. –№ 5. –С.24–28.
- Гасанов И. Р., Таирова С. А., Гасанов Р. И. Изучение особенностей проявления неньютоновских свойств углеводородов в процессе разработки и исследования методом установившихся отборов // Молодой ученый: Международный научный журнал. — Казань. –№ 22. –2016. –С.24–28.
- Гасанов И. Р., Таирова С. А., Гасанов Р. И. Методика интерпретации индикаторных линий скважин, добывающих углеводороды с аномальными свойствами // Научно-технический вестник. –Тверь: Каротажник. –№ 1. — 2017. –С.62–68.







