Моделирование асинхронного двигателя с переменными Ψm – IS на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink



Моделирование асинхронного двигателя с переменными Ψ_m – I_S на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink

Емельянов Александр Александрович, доцент;

Бесклеткин Виктор Викторович, ассистент;

Пестеров Дмитрий Ильич, студент;

Одинцов Василий Олегович, студент;

Соснин Александр Сергеевич, студент;

Антоненко Илья Александрович, студент;

Коновалов Илья Дмитриевич, студент;

Бабкин Виталий Андреевич, студент.

Российский государственный профессионально-педагогический университет

(г. Екатеринбург)

Данная работа является продолжением статьи [1]. Проекции векторов и выведены на основе интегрирующих звеньев с моделированием в Simulink.

В работе [1] было получено уравнение (9) для расчета тока I_Sx в Simulink-Script:

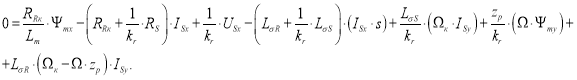
Перенесем в левую часть:

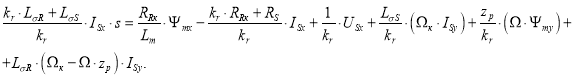
Обозначим и

Умножим обе части полученного уравнения на k_r:

Ток I_Sx определится в следующем виде:

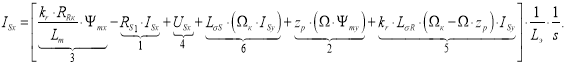
Структурная схема для определения тока I_Sx представлена на рис. 1.

Трансформируем структурную схему на рис. 1 в оболочку, позволяющую производить расчет коэффициентов в отдельном блоке Subsystem. Для этого установим блоки перемножения, к которым подведены сигналы с результатами расчетов в Simulink, как показано на рис. 2.

Рис. 1. Структурная схема для определения тока I_Sx в Script-Simulink

Рис. 2. Структурная схема для определения тока I_Sx в Simulink

Произведем аналогичную трансформацию при определении вектора тока по проекции y. В работе [1] получено следующее уравнение (11):

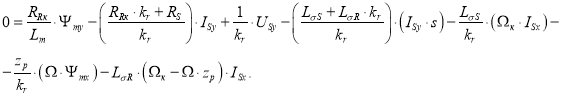
Перенесем в левую часть и умножим обе части на k_r:

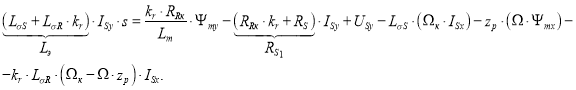
Определим ток I_Sy:

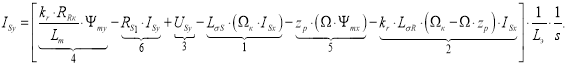
Структурная схема для определения тока I_Sy приведена на рис. 3.

Рис. 3. Структурная схема для определения тока I_Sy в Script-Simulink

Расчет коэффициентов будем производить в отдельном блоке Subsystem, поэтому вносим в структурную схему на рис. 3 блоки перемножения (рис. 4).

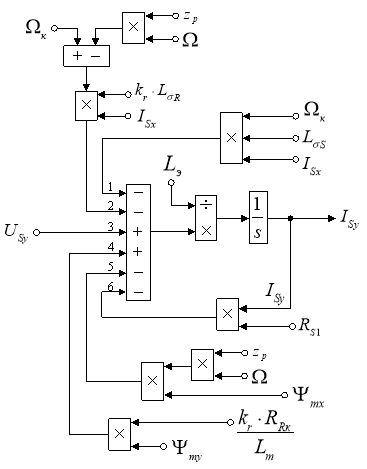
Рис. 4. Структурная схема для определения I_Sy в Simulink

Определим потокосцепление Ψ_mx по оси (+1) из уравнения (13) работы [1]:

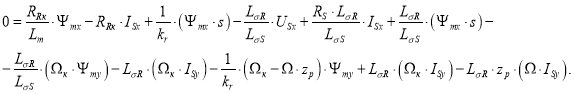
Перенесем в левую часть :

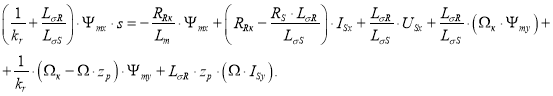
Обозначим:

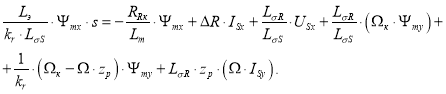
Определим потокосцепление Ψ_mx:

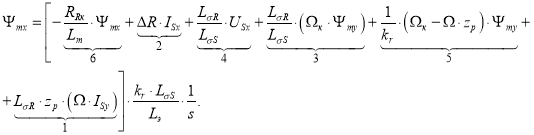
Структурная схема для определения потокосцепления Ψ_mx приведена на рис. 5. Подготовим эту схему для расчета в Simulink (рис. 6).

Рис. 5. Структурная схема для определения потокосцепления Ψ_mx в Script-Simulink

Рис. 6. Структурная схема определения Ψ_mx в Simulink

Аналогично определим потокосцепление Ψ_my по оси (+j) из уравнения (15) [1]:

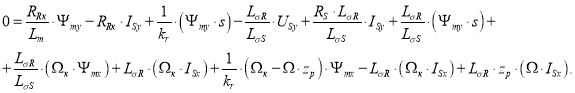
Перенесем в левую часть :

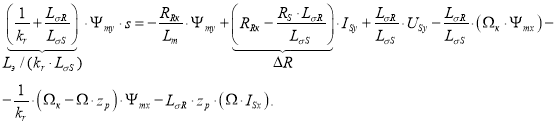
Тогда потокосцепление Ψ_my определится следующим образом:

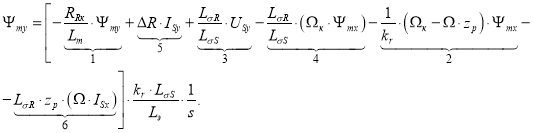
Структурная схема для определения потокосцепления Ψ_my приведена на рис. 7.

Рис. 7. Структурная схема для определения потокосцепления Ψ_my в Script-Simulink

Схема для расчета Ψ_my в Simulink представлена на рис. 8.

Рис. 8. Структурная схема для определения Ψ_my в Simulink

На рис. 9 представлена структурная схема для реализации уравнения электромагнитного момента в Simulink:

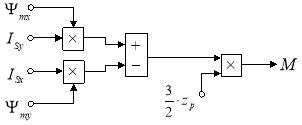
Рис. 9. Математическая модель определения электромагнитного момента M в Simulink

Структурная схема скорости вращения вала двигателя приведена на рис. 10:

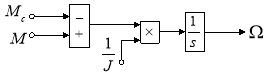
Рис. 10. Математическая модель уравнения движения в Simulink

Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными Ψ_m – I_S на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink дана на рис. 11, …, 15.

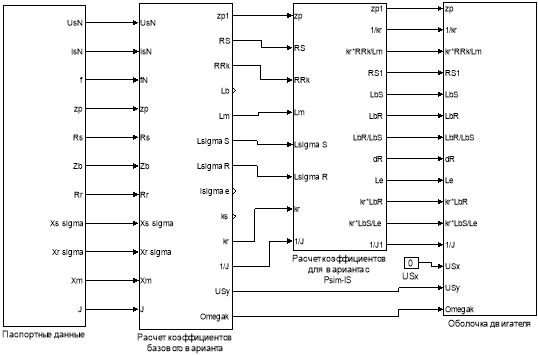
Рис. 11. Общая схема математической модели асинхронного двигателя с переменными
Ψ_m – I_S на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink

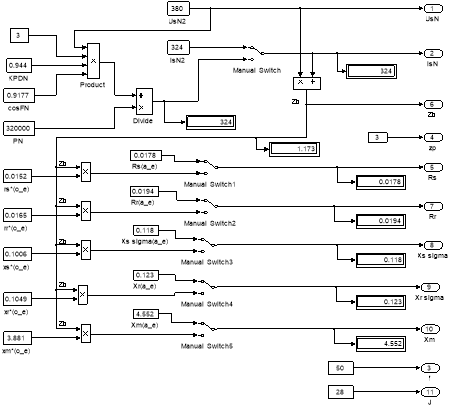
Рис. 12. Паспортные данные

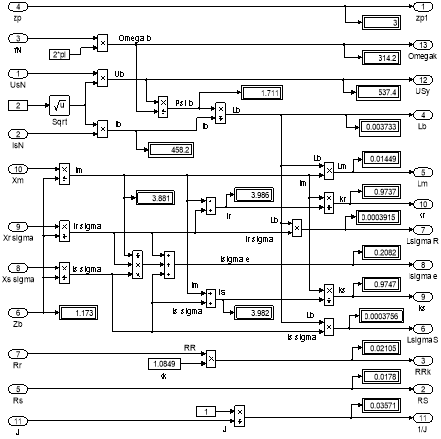
Рис. 13. Расчет коэффициентов базового варианта

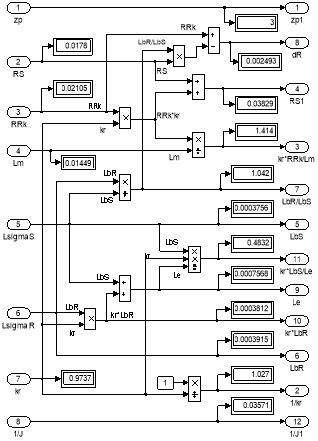
Рис. 14. Расчет коэффициентов для варианта с переменными Ψ_m – I_S

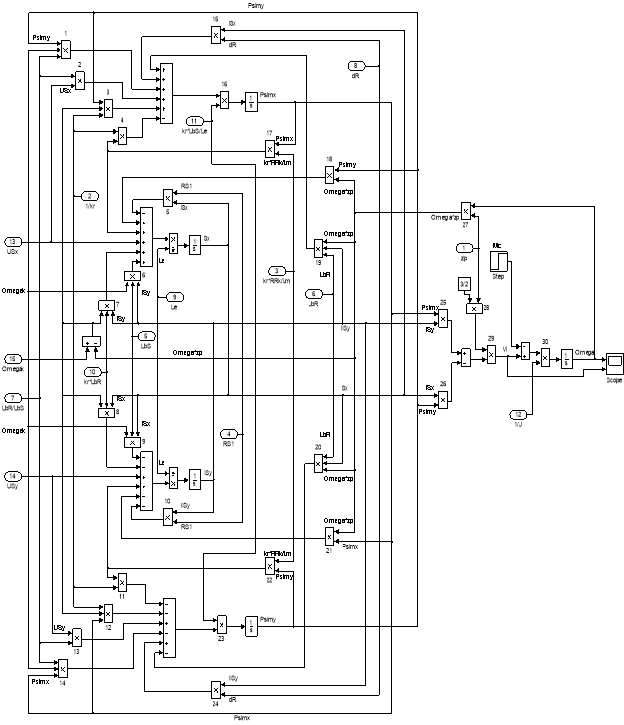
Рис. 15. Оболочка модели асинхронного двигателя с переменными Ψ_m – I_S на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink

Эту же схему можно представить в более компактной форме с использованием блоков Goto и From (рис. 16) и отдельных субблоков с расчетами токов и потокосцеплений, приведенных на рис. 17 и 18.

Результаты моделирования асинхронного двигателя представлены на рис. 19.

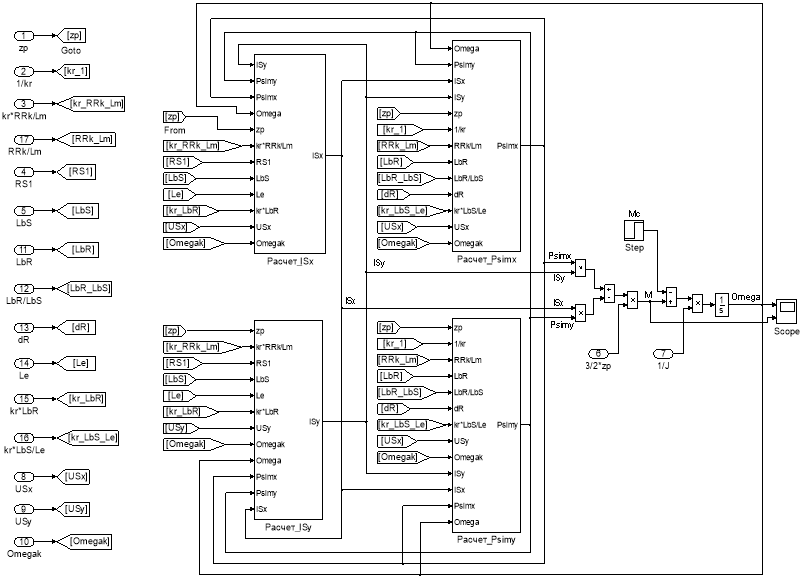
Рис. 16. Оболочка модели асинхронного двигателя с применением блоков Goto и From

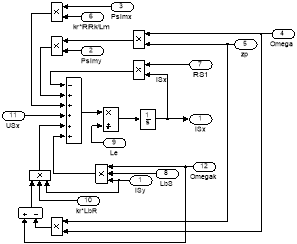
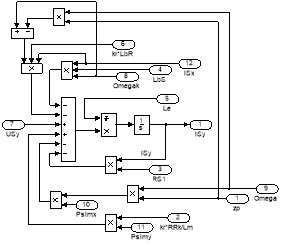
Рис. 17. Схемы для расчета I_Sx и I_Sy

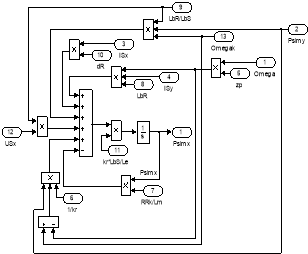
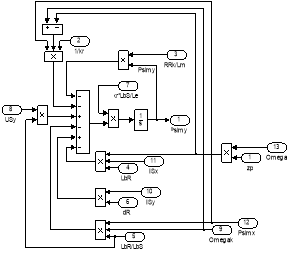
Рис. 18. Схемы для расчета Ψ_mx и Ψ_my

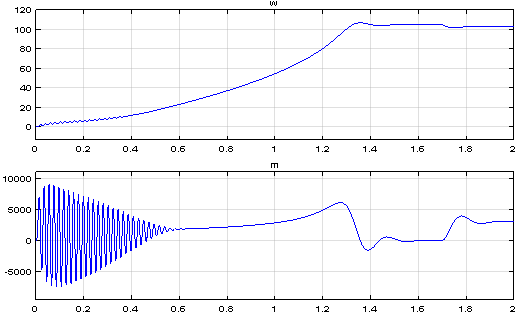
Рис. 19. Графики скорости и момента

Литература:

1. Емельянов А.А., Бесклеткин В.В., Пестеров Д.И., Одинцов В.О., Антоненко И.А., Коновалов И.Д., Бабкин В.А. Моделирование асинхронного двигателя с переменными Ψ_m – I_S на выходе апериодических звеньев в системе абсолютных единиц в Simulink-Script // Молодой ученый. - 2017. - №45. – С. 8-19.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
3. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.