В работе показано, что для стационарного притока углеводородов к скважине с учетом статического градиента давления в существующей формуле 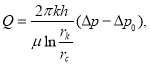 где
где ![]() вместо последнего выражения для
вместо последнего выражения для![]() должно быть выражение
должно быть выражение 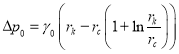 , а вместо распределения давления в виде
, а вместо распределения давления в виде![]() где
где ![]() должна быть формула
должна быть формула 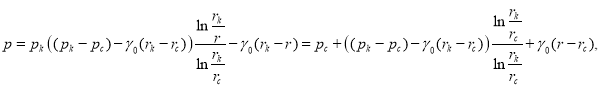 где
где ![]() . При этом разница между значениями дебита и распределения давления, которая вычислена разными формулами незначительна, однако качественное различие существует.
. При этом разница между значениями дебита и распределения давления, которая вычислена разными формулами незначительна, однако качественное различие существует.
Ключевые слова: начальный градиент, дебит, распределение давления, стационарный приток
It is shown that for a steady flow of hydrocarbons to the well, taking into account the static pressure gradient in the existing formula 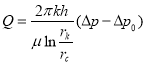 where
where ![]() instead of the last expression for
instead of the last expression for ![]() should be an expression
should be an expression 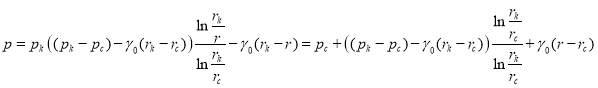 And instead of the distribution of pressure in the form,
And instead of the distribution of pressure in the form, ![]() where
where ![]() there should be a formula in the form
there should be a formula in the form 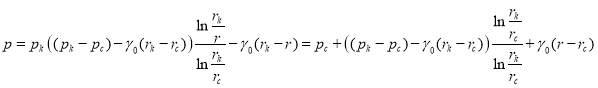 where
where ![]() . In this case, the difference between the values of flow rate and pressure distribution, which are calculated by different formulas, are insignificant, but there is a qualitative difference.
. In this case, the difference between the values of flow rate and pressure distribution, which are calculated by different formulas, are insignificant, but there is a qualitative difference.
Keywords: initial gradient, flow rate, pressure distribution, stationary inflow
При установившемся движении несжимаемой жидкости с учетом статического градиента давления расход Q сохраняется вдоль оси r струйки. Тогда ![]() и
и 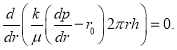 Последнее, сокращая на постоянные величины
Последнее, сокращая на постоянные величины ![]() , получаем:
, получаем:
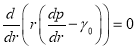 . (1)
. (1)
Дважды проинтегрировав уравнение (1), получим его общее решение. Находим последовательно:
![]() или
или ![]() (2)
(2)
Постоянные интегрирования ![]() и
и ![]() находятся из граничных условий, которые в данном случае можно записать в виде:
находятся из граничных условий, которые в данном случае можно записать в виде:
![]() при
при ![]() , (3)
, (3)
![]() при
при ![]()
Подставляя граничные условия в общее решение (2), находим:
![]() ,
,
![]() ,
,
откуда
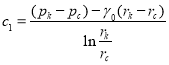 , (4)
, (4)
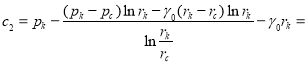
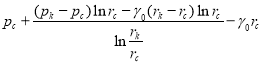 (5)
(5)
Подставляя (4) и (5) в общее решение (2), получаем закон распределения давления в плоскорадиальном потоке:
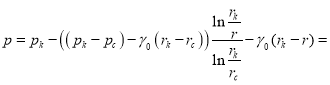
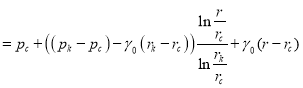 . (6)
. (6)
Градиент давления ![]() определим из (2), подставив в него значение
определим из (2), подставив в него значение ![]() из (4):
из (4):
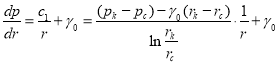 . (7)
. (7)
Тогда скорость фильтрации и дебит скважины соответственно будут:
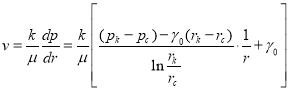 (8)
(8)
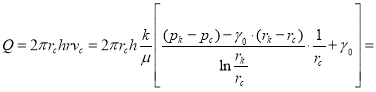
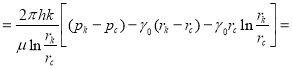 (9)
(9)
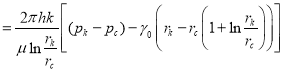 .
.
Здесь, подставив 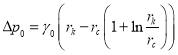 в (9), получаем:
в (9), получаем:
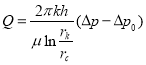 . (10)
. (10)
Это — точная формула для стационарного притока углеводородов к скважине с учетом статического градиента давления. Если его сравнить с формулой [1, 2]:
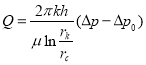 , где
, где
то видим, что в формуле (10) ![]() зависит от радиусов линейно. А в формуле (9) эта зависимость имеет нелинейный характер. Если сравнить формулы для распределения давления без начального градиента с начальным градиентом по (6) и с существующей формулой для распределения давления
зависит от радиусов линейно. А в формуле (9) эта зависимость имеет нелинейный характер. Если сравнить формулы для распределения давления без начального градиента с начальным градиентом по (6) и с существующей формулой для распределения давления
![]() , (12)
, (12)
то получаем, что графический вид распределения давления по формуле (6) в начале находится выше, чем по формуле (12), а в дальнейшем с увеличением радиуса ![]() они практически совпадают (рис.1). Если сравнить дебиты по формулам (9) и (11), то они также почти полностью совпадают.
они практически совпадают (рис.1). Если сравнить дебиты по формулам (9) и (11), то они также почти полностью совпадают.
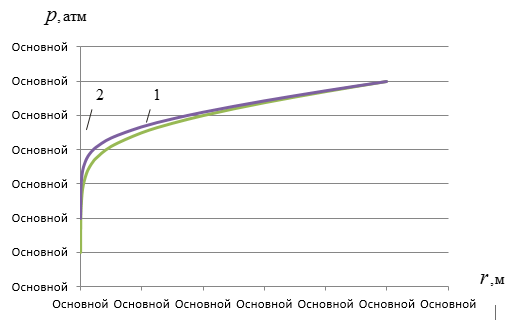
Рис.1. Кривые распределения давления: 1 — по формуле (12); 2 — по формуле (6)
Действительно, если обозначим полученный нами дебит через ![]() , то для различных значений входящие в них параметры значений выражения
, то для различных значений входящие в них параметры значений выражения ![]() составляют меньше 1 %. Полученные небольшие расхождения связаны с тем, что распределение давления по формуле (12), вообще говоря, не удовлетворяет условиям (3). То есть при
составляют меньше 1 %. Полученные небольшие расхождения связаны с тем, что распределение давления по формуле (12), вообще говоря, не удовлетворяет условиям (3). То есть при ![]() получается
получается ![]() , однако при
, однако при ![]() . Формула (11) получена из формулы (12) при
. Формула (11) получена из формулы (12) при ![]() и
и ![]() . Несмотря на то что, при
. Несмотря на то что, при ![]() по формуле (12) вообще говоря
по формуле (12) вообще говоря ![]() , это не влияет на значение дебита, так как значение
, это не влияет на значение дебита, так как значение ![]() и значение
и значение ![]() находится под знаком натурального логарифма. То есть выражения
находится под знаком натурального логарифма. То есть выражения ![]() и
и ![]() при различных возможных значениях
при различных возможных значениях ![]() при
при ![]() мало отличаются друг от друга.
мало отличаются друг от друга.
Литература:
- Мирзаджанзаде А. Х., Ковалев А. Г., Зайцев Ю. В. Особенности эксплуатации месторождений аномальных нефтей. — М.: Недра, 1972. — С.200.
- Мирзаджанзаде А. Х., Гурбанов Р. С. Обзор работ по гидродинамике вязкопластичных сред в бурении. –Баку, 1968. — 83 с.







