В статье проведен полный факторный эксперимент участка на подходе к кольцу ВПЗ со стороны ул. Пушкина г. Волжский и доказана целесообразность его совершенствования, произведена проверка по критерию Стьюдента и Фишера.
Ключевые слова: пересечение, эксперимент, организация дорожного движения, безопасность дорожного движения
Пересечения автомобильных дорог в одном уровне входят в перечень наиболее опасных участков улично-дорожной сети с вытекающими негативными последствиями в виде: уменьшение пропускной способности дорог, снижение скорости движения автомобилей и концентрации дорожно-транспортных происшествий.
Улично-дорожная сеть г. Волжский состоит в продольном плане из пяти основных улиц: пр. Ленина, ул. Карбышева, ул. Дружбы, ул. Мира и ул. Пушкина. Основные заторовые ситуации на продольных улицах наблюдаются по времени — в часы пик, по месту расположению — на участках улиц, расположенных вблизи центров тяготения населения (крупных торгово-развлекательных центров, например, Планета Лето, Простор, Гранд, крупных социальных учреждений, например, Городская больница № 1, Стоматологическая поликлиника)
Актуальность работы в следующем. Исследуемый участок кольцо ВПЗ один из наиболее проблемных участков улично-дорожной сети г. Волжский. Проблемы заключаются в нестандартной организации дорожного движения на кольце и как следствие возникновению ДТП, возникающих по причине несоблюдения очередности проезда пересечения, больших транспортных задержек по ул. Пушкина и 7-й Автодороге в часы пик. Целью данной работы является повышение безопасности дорожного движения на рассматриваемом участке УДС путем изменения организации дорожного движения, направленных на снижение числа ДТП и уменьшения транспортных задержек по ул. Пушкина.
Рассматриваемый участок УДС — подход к кольцевому пересечению ВПЗ по стороны ул. Пушкина (поворот на оптовую базу). Так как данное кольцевое пересечение является местом слияния транспортных потоков промышленного и торгового сектора, то формирование заторовой ситуации на участке обычное дело.
Данный участок УДС, при проектировке не был рассчитан на высокую интенсивность движения по рассматриваемым направлениям, возникшую вследствие развития инфраструктуры города в направлении, отличающемся от первоначального. Это привело к слиянию основных транспортных потоков города на рассматриваемом участке, а значит к более высокой аварийности и в конечном итоге к заторам. Причем высокая аварийность сохраняется не только в часы пик, но и в любое другое время за счет неоднородности приоритета движения. На рисунке 1 представлено рассматриваемое пересечение.
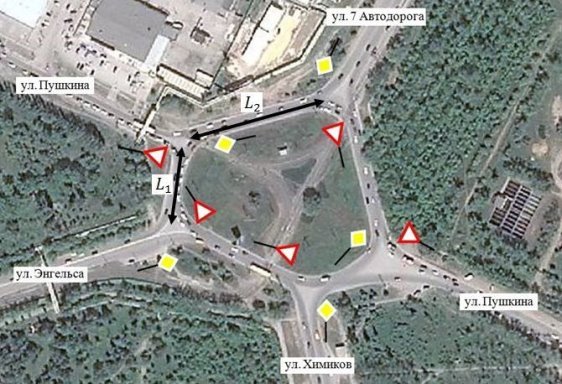
Рис. 1. Рассматриваемый участок улично-дорожной сети
Через данный участок УДС проходят основные рабочего транспорта города во всех направлениях. В пределах этого участка УДС находится «Оптовая база» и трамвайное «кольцо». Так же велик объем частных транспортных средств, проходящих через данный транспортный узел. Ко всему прочему, на данном участке УДС организовано «сложное и непонятно» движение по кольцу. В связи с этим движение через данный транспортный узел затруднительно.
В данной работе изучается влияние на задержки автомобильного транспорта на подходе к кольцевому пересечению ВПЗ, улице Пушкина, трех факторов:
– сумма длин подходов (![]() +
+ ![]() ) в диапазоне 119–153 м.;
) в диапазоне 119–153 м.;
– интенсивность движения на подходе в диапазоне 500–700 транспортных средств за час;
– длительность красной фазы светофора на подходе к пересечению в диапазоне 0–22 сек.
На рисунке 2 показан рассматриваемый участок, построенный в программе Aimsun, где № 1 и 2 — номера светофоров.
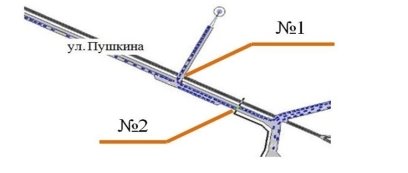
Рис. 2. Модель рассматриваемого участка по ул. Пушкина
Большое количество экспериментальных задач формируются как задачи экспериментальные: определение оптимальных условий процесса и т. д. Благодаря оптимальному расположению точек вфактором пространстве и линейному преобразованию координат, удается преодолеть недостатки классического регрессионного анализа, в частности корреляцию между коэффициентами уравнения регрессии. Выбор плана эксперимента определяется постановкой задачи исследования и особенностями объекта. Процесс исследования обычно разбивается на отдельные этапы. Информация, полученная после каждого этапа, определяет дальнейшую стратегию эксперимента. Таким образом возникает возможность оптимального управления экспериментом. Планирование эксперимента позволяет варьировать одновременно все факторы и получать количественные оценки основных эффектов и эффектов взаимодействия. В конечном счете применение методов планирования значительно повышает эффективность эксперимента.
Верхний уровень по длине подхода ![]() равен 153, нижний
равен 153, нижний ![]() равен 119. Тогда для
равен 119. Тогда для ![]() имеем:
имеем:
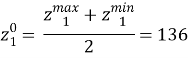
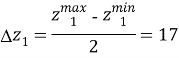
Аналогично для любого фактора
Точка с координатами (![]() , …,
, …, ![]() ) называется центром плана, иногда ее называют основным уровнем;
) называется центром плана, иногда ее называют основным уровнем; ![]() — интервал варьирования по оси
— интервал варьирования по оси ![]() . От переменных
. От переменных ![]() , …,
, …, ![]()
перейдем к новым — ![]() , …,
, …, ![]() путем следующего линейного преобразования:
путем следующего линейного преобразования:

j = 1, 2, …, k.
Для переменных ![]() , …,
, …, ![]() верхний уровень равен +1, нижний уровень -1, координаты центра плана равны нулю и совпадают с началом координат. В данной работе k=3. Число возможных комбинаций N из трех факторов на двух уровнях равно N=
верхний уровень равен +1, нижний уровень -1, координаты центра плана равны нулю и совпадают с началом координат. В данной работе k=3. Число возможных комбинаций N из трех факторов на двух уровнях равно N= ![]() =
=![]() =8. План проведения экспериментов (матрица планирования) записывается в виде табл. 1.
=8. План проведения экспериментов (матрица планирования) записывается в виде табл. 1.
Таблица 1
Полный факторный эксперимент
|
Номер опыта |
Факторы внатуральном масштабе |
Факторы вбезразмерном масштабе |
|||||
|
|
|
|
|
|
|
y |
|
|
1 |
119 |
500 |
0 |
-1 |
-1 |
-1 |
4,95 |
|
2 |
153 |
500 |
0 |
+1 |
-1 |
-1 |
4,65 |
|
3 |
119 |
700 |
0 |
-1 |
+1 |
-1 |
5,15 |
|
4 |
153 |
700 |
0 |
+1 |
+1 |
-1 |
4,82 |
|
5 |
119 |
500 |
22 |
-1 |
-1 |
+1 |
6,50 |
|
6 |
153 |
500 |
22 |
+1 |
-1 |
+1 |
6,55 |
|
7 |
119 |
700 |
22 |
-1 |
+1 |
+1 |
10,54 |
|
8 |
153 |
700 |
22 |
+1 |
+1 |
+1 |
8,99 |
Пользуясь планом, представленным в табл. 1, было построено уравнение регрессии и вычислены его коэффициенты:
Y = ![]() +
+![]() +
+![]() +
+![]() ,
,
Где b — коэффициент уравнения регрессии;
x — фактор в безразмерном масштабе.
Далее в рассмотрение было получено полное уравнение регрессии с коэффициентами взаимодействия:
Y = ![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]()
После исключения незначимых коэффициентов уравнении регрессии с помощью критерия Стьюдента оно имеет вид:
Y = 6,52+![]() +
+![]() +
+![]()
Проверим адекватность полученного уравнения по критерию Фишера:
F=![]() /
/![]() ;
;
![]() =
=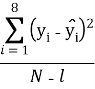 =
=![]() =0,33
=0,33
![]() =0,21
=0,21
l — число значимых коэффициентов в уравнении регрессии, равное 4. Тогда,
F=0,33/0,21=1,6
Табулированное значение критерия Фишера для p=0,05,
F<![]() (
(![]() ,
,![]() ), 1,6<19,25
), 1,6<19,25
Следовательно, полученное уравнение адекватно описывает эксперимент.
Так как для расчетов необходимы конкретные значения, от переменных ![]() , …,
, …, ![]() перейдем к старым переменным -
перейдем к старым переменным -![]() , …,
, …, ![]() путем следующего линейного преобразования линейного уравнения регрессии, без учета незначимых коэффициентов:
путем следующего линейного преобразования линейного уравнения регрессии, без учета незначимых коэффициентов:
Y = 6,52 + 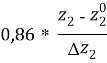 +
+ 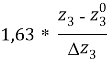 +
+ 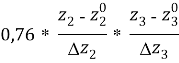
То линейное уравнение регрессии примет вид:
Y = 6,52 + 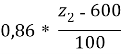 +
+ 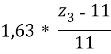 +
+ 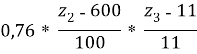
После упрощения уравнение регрессии будет выглядеть:
Y = 4,35–0,27![]() + 0,0007
+ 0,0007![]()
Представим полученные значения в сводной таблице 2:
Таблица 2
Сравнительная таблица теоретических иопытных значений Y
|
|
|
|
|
1 |
4,95 |
4,35 |
|
2 |
4,65 |
4,35 |
|
3 |
5,15 |
4,35 |
|
4 |
4,82 |
4,35 |
|
5 |
6,50 |
6,11 |
|
6 |
6,55 |
6,11 |
|
7 |
10,54 |
9,19 |
|
8 |
8,99 |
9,19 |
Вывод
После проведения полного факторного эксперимента на основе полученных данных о средних задержках из программы и при проверке его критерием Стьюдента были выявлены четыре незначимых коэффициента ![]() ,
, ![]() ,
, ![]() ,
, ![]() , которые следовало исключить из уравнения регрессии. В дальнейшем адекватность полученного уравнения была проверена по критерию Фишера, в ходе которого было доказано, что полученное уравнение регрессии адекватно описывает эксперимент F<
, которые следовало исключить из уравнения регрессии. В дальнейшем адекватность полученного уравнения была проверена по критерию Фишера, в ходе которого было доказано, что полученное уравнение регрессии адекватно описывает эксперимент F<![]() (
(![]() ,
,![]() ), 1,6<19,25.
), 1,6<19,25.
Для удобства расчета линейное уравнение регрессии, путем преобразований, было переведено в первоначальный вид и упрощено:
Y = 4,35–0,27![]() + 0,0007
+ 0,0007![]()
Подставив искомые значения коэффициентов ![]() получились новые значения Y. При сравнении теоретических и практических значений Y видно, что они приблизительно похожи.
получились новые значения Y. При сравнении теоретических и практических значений Y видно, что они приблизительно похожи.
Полученные данные подтверждают теоретические предположения и значения, полученные из программы. Наиболее низкие средние задержки будут при:
– увеличении длины подходов от 119 — до 153 м.;
– уменьшении интенсивность движения до 500 транспортных средств за час;
– полном демонтаже пешеходного светофора на подходи к кольцевому пересечению.
Литература:
1 Автомобильные дороги и улицы [Электронный ресурс]: гос. Стандарт РФ от 11.10.1993 № 221. — Доступ из справ. — правовой системы «Консультант Плюс».
2 Клепик, Н. К. Дорожные условия и безопасность движения: учеб. пособие / Н. К. Клепик, Е. И. Железнов; — ВолгГТУ. — Волгоград, 1997. — 61 с.
3 Клинковштейн, Г. И. Организация дорожного движения: учебник для вузов / Г. И. Клинковштейн, М. Б. Афанасьев. — 5-е изд. перераб. и доп. — Москва: Транспорт, 2001. — 106 с.
4 Коноплянко, В. И. Организация и безопасность дорожного движения: учебник для вузов / под ред. В. И. Коноплянко — Москва: Транспорт, 1991. — 183 с.
5 Сильченков, Д. Д. Применение современных методов проектирования при организации дорожного движения: учеб. пособие / Д. Д. Сильченков, Р. Р. Санжапов, А. В. Шустов; ВолгГТУ. — Волгоград, 2015. — 95 с.







