В статье изложены основные вопросы определения компонентов топологической диаграммы путевой структуры любого железнодорожного узла с помощью полиномиального инварианта Джонса. Представленный способ расчета основан на методах теории узлов и может быть использован для определения оптимальных вариантов узловых путевых структур с использованием известных комбинаторных алгоритмов.
Ключевые слова: железнодорожный узел, ориентированный узел, преобразования Рейдемейстера, скобка Кауфмана, полином Джонса
Железнодорожные узлы являются важнейшими звеньями в организации и пропуске поездопотоков, и по праву считаются высшей ступенью инфраструктуры и транспортной интеграции.
Известно, что железнодорожным узлом называется пункт пересечения или примыкания нескольких линий, объединяющих ряд связанных между собой соединительными ветвями различных по назначению станций, работающих по единой технологии.
Наиболее актуальной задачей в изучении железнодорожных узлов является разработка алгоритма построения и оценки различных узловых путевых структур для обеспечения эффективной организации их работы по продвижению поездопотоков.
В современных задачах проектирования и построения развязок узловых путевых структур важным подходом к выявлению вариантов возможного соединения путей является классический комбинаторный анализ. К сожалению, такой подход позволяет определить лишь возможное число вариантов и требует алгоритмического моделирования на компьютере для выявления и перебора путевых структур соединения линий, но изначально ничего не говорит о самих характеристиках этих структур.
Создание метода оценки узловых путевых структур и степени организации технологических процессов возможно на основе создания новых критериев их оценки с использованием маломерно-топологических принципов теории узлов и теории кос, а также применения комбинаторного анализа для выявления оптимальной их путевой структуры при проектировании новых узлов и проведении по существующим железнодорожным узлам реконструкционных мероприятий.
Определяющим принципом маломерно-топологических методов проектирования и реконструкции является преобразование геометрических схем железнодорожных узлов в алгебраические путем введения довольно простых и естественных объектов алгебро-геометрического характера. Оказывается, этот прием чрезвычайно полезен в первую очередь тем, что позволяет применить для исследования геометрических свойств путевого развития железнодорожных узлов возможности методов алгебры.
В частности, используя этот прием можно определять те или иные качественные топологические характеристики железнодорожных узлов, сравнивать их между собой и применять комбинаторные алгоритмы для более эффективного преобразования одной схемы узла в другую. Остановимся на изложении некоторых основных понятий маломерно-топологических методов моделирования реконструкционных схем путевого развития развязок линий в железнодорожных узлах
На первом этапе путевая схема развязки линий моделируется в виде топологического узла путем соединения путей друг с другом. При этом должно выполняться условие, при котором соединения не должны образовывать новых двойных точек самопересечения. Полученные смоделированные топологические многообразия могут включать в себя как тривиальные и нетривиальные узлы, так и зацепление Хопфа [2, с. 11].
На втором тапе смоделированные топологические узлы превращаются в узлы-обмотки (путем применения алгоритма Вожеля [2, с. 107]) и расправляются в математическую косу с выявлением всей ее алгебраической структуры.
На третьем этапе моделирования проводится комбинаторный анализ для выявления всех вариантов соединения путей в развязке посредством применения соотношений Артина для всех возможных третьих движений Рейдемейстера [1, с. 21].
Один из наиболее важных вопросов моделирования узловых путевых структур в виде топологических диаграмм связан с тем, чтобы по заданным диаграммам определить, каким тривиальным и нетривиальным компонентам они соответствуют. Стандартный метод заключается в использовании полиномиальных инвариантов. На рис. 1 представлен пример схемы простейшей узловой путевой структуры и ее топологическая диаграмма.
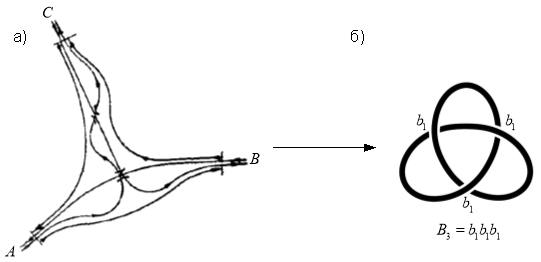
Рис. 1. Пример представления схемы развязки подходов железнодорожных линий в узлах треугольного типа: 
в общепринятом — геометрическом виде; 
в алгебраическом — в виде топологического узла
Построение полинома Джонса [3] мы начнем с того, что сопоставим каждой диаграмме 
неориентированного топологического узла полином 
, предложенный Луисом Кауффманом в работе [4]. Сопоставим топологической диаграмме предложенного примера такую скобку Кауфмана, чтобы выполнялись следующие соотношения:
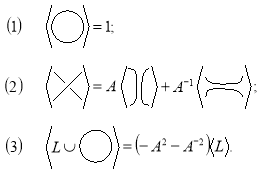
Рассчитаем скобку Кауффмана для топологической диаграммы представленной развязки следующим образом:
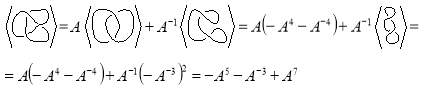
Теперь мы можем построить полином Джонса, который инвариантен относительно всех трех преобразований Рейдемейстера:
Тип I. Скручивание и раскручивание в любом направлении.
Тип II. Перемещение одной петли целиком через другую.
Тип III. Перемещение нити целиком над или под пересечением.
Следует иметь ввиду, что в комбинаторном анализе при определении числа вариантов возможного соединения линий в развязке железнодорожного узла применяется третье движение Рейдемейстера (рис. 2)
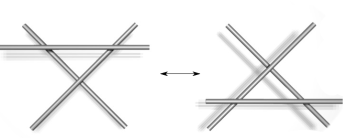
Рис. 2. Графическое представление третьего движения Рейдемейстера
Определение. Ориентированным узлом называется узел, на котором задано направление обхода, или же отображения ориентированной окружности в 
. При этом при изотопии узлов требуется условие сохранения ориентации.
Задав направление обхода на топологической диаграмме (рис. 3), число ее закрученности будет
.
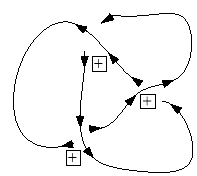
Рис. 3. Определение числа закрученности на топологической диаграмме
Отсюда полином Джонса будет равен:
Применяем другую форму записи полинома Джонса:
. Получим
.
Таким образом, можно сделать вывод, что представленный пример топологической диаграммы железнодорожного узла треугольного типа является «трилистником». Предложенный способ позволяет определить все компоненты (тривиальные и нетривиальные) топологической диаграммы. Дальнейшие рассуждения об использовании множества компонентов диаграммы к нахождению всех возможных вариантов конструкций развязок будут касаться комбинаторных алгоритмов с учетов применения всех возможных третьих преобразований Рейдемейстера.
Литература:
- Кассель К, Тураев В. Г. Группы кос / Перевод с англ. С. Н. Малыгина. ‒ М.: МЦНМО, 2014. ‒ 422 с.
- Мантуров О. Н. Лекции по теории узлов и их инвариантов. ‒ М.: Эдиториал УРСС, 2001. ‒ 304 с.
- V. F. R. Jones. Apolynomial invariant for links via von Neumann algebras, Bull. Amer. Soc. 129 (1985), 103–112.
- L. H. Kauffman. On Knots, Annals of Math Stodies, Princeton Univ. Press, 1987.
