При решении трёхмерных прямых и обратных задач МТЗ возникают проблемы, связанные с необходимостью длительных и сложных расчётов. В процессе обработки данных МТ для каждой точки наблюдения расчитывают частотные зависимости модулей и фаз компонент тензора импеданса. Анализ этих кривых позволяет оценить наличие искажений, обусловленных горизонтальной неоднородностью разреза. В частности они могут быть вызваны как латеральными неоднородностями электропроводности среды, так и неровностью рельефа местности [1, 2]. Интерпретация кривых МТЗ без учёта вышеупомянутых искажений может привести к получению информации о недрах земли, не соответствующий реальности и построению недостоверных геоэлектрических разрезов.
Вышеупомянутые искажения проявляются под действием гальванических и индукционных эффектов [3]. Гальванические искажения обусловлены действием избыточных зарядов, которые возникают на неоднородностях электропроводности среды. Они проявляются на малых частотах зондирования. Индукционные искажения связаны с действием избыточных токов в среде. Они наблюдаются на больших частотах зондирования. В ряде работ [4] гальванический эффект называют так же S-эффектом (так как искажения кривых МТЗ на больших периодах зондирования определяются степенью неоднородности суммарной продольной проводимости разреза [5]), а искажения кривых статическими. Если гальванический эффект вызван мелкими приповерхностными неоднородностями электропроводности, то его называют ρ-эффектом. При гальваническом эффекте искажённая кривая кажущегося сопротивления сдвинута по оси сопротивлений параллельно относительно локально-нормальной кривой, а фазовые искажённая и неискажённая кривые совпадают. При индукционном эффекте закономерности в расположении искажённых кривых МТЗ относительно неискажённых имеют более сложный характер. Его действие нередко приводит к появлению дополнительных минимумов (максимумов) на кривых кажущегося сопротивления — эффект ложного проводящего (высокоомного) слоя [6].
Особенности гальванических и индукционных искажений проявляются при нахождении аналитического решения прямой задачи для двумерной или трёхмерной модели среды. Известно множество способов устранения гальванических искажений кривых МТЗ и дальнейшей обработки полевых данных с помощью одномерной инверсии. В работе [7] предлагаются следующие способы устранения искажений: сдвиг кривых МТЗ, пространственная фильтрация, применение тензора искажений и моделирование. В статье [8] для подавления гальванических искажений рассмотрен способ обработки данных МТЗ с привлечением лишь TE-моды (![]() ) электромагнитного поля и исключением TM-моды (
) электромагнитного поля и исключением TM-моды (![]() ). Обосновано это тем, что TM-мода появляется в горизонтально-неоднородных средах.
). Обосновано это тем, что TM-мода появляется в горизонтально-неоднородных средах.
В данной работе рассматривается использование МТЗ совместно с М-ЗСБ, которая имеет «иммунитет» к гальваническим искажениям и позволяет учесть неоднородность ВЧР и оценить параметры глубинных объектов.
Рассмотрим технологию комплексной интерпретации электроразведочных данных М-ЗСБ и МТЗ на примере модели, построенной на вдоль профиля (рис. 1). Для моделирования среды использовался программный комплекс EM-DataProcessor (ЗАО «Аэрогеофизическая разведка»). Шаг наблюдения МТЗ — 1000 м, М-ЗСБ -500 м. Диаметр приемной петли в методе М-ЗСБ — 1 м, размер генераторной — 100х100 м, расстояние между генераторными петлями — 3500 м. Так как в методе М-ЗСБ регистрируется вторичное электромагнитное поле, то ее результаты не подвержены локальным поверхностным аномалиям и топографическим условиям. Также данный метод обладает достаточно высоким разрешением до глубины 500 м и поэтому более эффективно обнаруживает мелкие аномальные зоны по сравнению с МТЗ.
Как видно из рис. 1 моделируемая среда, состоящая из трех аномальных объектов, расположеных на гбуине ниже 3000 м осложнена приповерхностными неоднородностями.
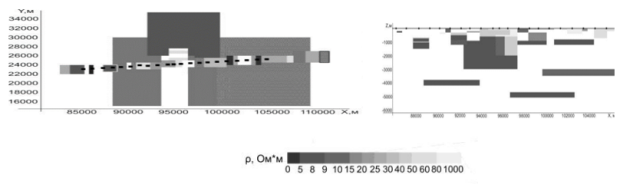
Рис. 1. Модель среды
На рис. 2 представлена кривая сопротивления и геоэлектрический разрез по данным автоматической 1D-инверсии данных МТЗ по профилю, из которого видно, что без нормализации данных МТЗ интерпретировать полученный разрез не представляется возможным. Из за смещения кривой МТЗ в геоэлектрическом разрезе отсутсвуют глубинные аномалии, а поверхностные аномалии локализованы не корректно. Для того, чтобы компенсировать смещение графиков кажущихся сопротивлений, возникающих из-за локальных неоднородностей в ВЧР в большинство случаев прибегают к нормализации данных МТЗ.

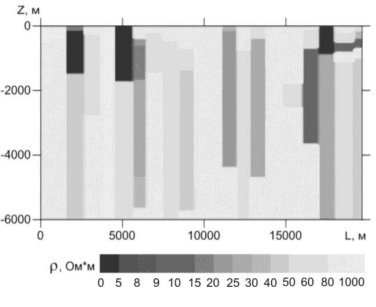
Рис. 2. кривая сопротивления и геоэлектрический разрез по данным 1D-инверсии данных МТЗ
При наличии только данных МТЗ нормализация проводится по среднему уровню в группе схожих кривых (близких по фазам). При такой нормализации искажается информация о ВЧР, которая хотя и не является целевым объектом исследования, но ее неточное восстановление может привести к существенному искажению глубинной части геоэлектрического разреза. Наиболее же корректным способом нормализации является использование данных М-ЗСБ, которые либо практически не реагируют на такого рода объекты — помехи, либо дают достаточную информацию для их корректного учета. Поэтому следующим этапом интерпретации комплекса данных М-ЗСБ и МТЗ является обработка данных М-ЗСБ, после которой получаем кривую сопротивления (рис 3), отличающиеся от траектории кривой МТЗ на аналогичных частотах.
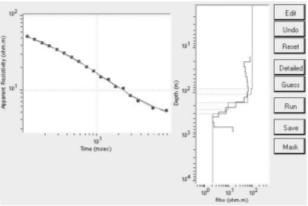
Рис. 3. кривая сопротивления по данным М-ЗСБ
Так как данные М-ЗСБ менее подвержены воздействию локальных неоднородностей рельефа и промышленных помех она является базовой кривой, на которую и делается сдвиг кривых МТЗ по методу Бостика [9]. После нормализации данных МТЗ с учетом сдвига по М-ЗСБ получим кривые, изображенные на рис. 4.
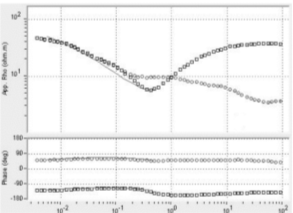
Рис. 4. Нормализованная кривая МТЗ
Для детальной параметризации разреза далее проводится 3D-интерпретация данных МТЗ с фиксированной 3D-моделью ВЧР, полученной по данным М-ЗСБ. В результате инверсии данных МТЗ получаем геоэлектрический разрез, показанный на рис. 5, более качественно локализующая как поверхностные, так и глубинные аномалии.
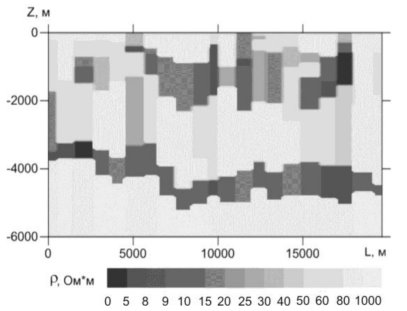
Рис. 5. геоэлектрический разрез по результатам 1D-инверсии нормированных данных МТЗ
Из всего вышеперечисленного следует, что комплексная обработка данных М-ЗСБ и МТЗ в программном обеспечении EM-DataProcessor позволяет повысить разрешение объемной реконструкции глубинной части разреза за счет более детального восстановления неоднородной ВЧР по данным М-ЗСБ, нормализации данных МТЗ на основе полученной модели верхней части разреза.
Литература:
- Jiracek G. R. Near-surface and topographic distortions in electromagnetic induction // Surv. Geophys.. — 1990. — V. 11. — № 2–3. — P. 163–203.
- Плоткин В. В., Губин Д. И. Моделирование влияния рельефа при магнитотеллурическом зондировании // Интерэкспо ГЕО-Сибирь-2014. — [Электронное издание]. Новосибирск: СГГА. 2014. Сборник материалов. — Т. 2. — № 3. — С. 8–13.\
- Альпин Л. М. Теория поля. М.: Недра, 1966, 384 с.
- Berdichevsky M. N. and Dmitriev V. I., 1976, Basic principles of interpretation of magnetelluric sounding curves, In: A. Adam (ed), “Geoelectric and Geotermal Studies”, Akademiai Kiado, Budapest.
- Плоткин В. В., Губин Д. И. Моделирование влияния рельефа при магнитотеллурическом зондировании // Интерэкспо ГЕО-Сибирь-2014. — [Электронное издание]. Новосибирск: СГГА. 2014. Сборник материалов. — Т. 2. — № 3. — С. 8–13.
- Бердичевский М. Н., Дмитриев В. И. Модели и методы магнитотеллурики. М.: Научный мир, 2009, 680 с.
- Барашков А. С., Дмитриев В. И. Об обратной задаче глубинного магнитотеллурического зондирования // ДАН СССР. — 1987. — Т. 295. — № 1. — С. 83–86.
- Plotkin V. V. Synchronous magnetotelluric sounding with non-uniform source field excitation [Электронный ресурс] // Problems of Geocosmos: Proceedings of the 10th International Conference (St. Petersburg, Russia, October 6–10, 2014). — St. Petersburg, 2014. — P. 45–51.
- Bostick, EX.: A simple almost exact method of MT analysis. Workshop on Electrical Methods in Geothermal Exploration, U. S. Geol. Surv., Contract No. 14080001–8-359, 1977







