В данной статье рассмотрены методики анализа динамических погрешностей отработки программной траектории. На основе проведенного исследования автором предлагается блок-схема обобщенного алгоритма вычисления погрешности.
Ключевые слова: динамические погрешности, рабочая точка, программные траектории.
Предлагается следующая методика анализа динамических погрешностей.
- Формулирование требований к законам изменения координат рабочей точки и углов ориентации рабочего органа во времени (может быть, в различных системах координат и разных способах: координаты прямоугольные или иные, как функции времени, скорости, как функции времени или координат, или длины дуги, или координаты, как функции длины дуги, преимущества и недостатки представлений).
- Решение обратных задач геометрии и кинематики, определение программ изменения обобщенных координат и обобщенных скоростей тоже в различных формах (в зависимости от времени, условного параметра, длины дуги, друг от друга, что упрощает реализацию).
- Переход к законам перемещения выходных звеньев двигателей, определение законов перемещения выходных звеньев двигателей и соответствующих скоростей.
- Расчет составляющих вектора погрешностей для двигателя каждого привода в зависимости от времени.
- Расчет составляющих вектора погрешностей по программной траектории в зависимости от длины дуги или координат концевой точки.
- Расчет отклонений (в том числе максимальных), по заданным направлениям (в частности, по нормали и бинормали реальной траектории от программной траектории).
- Определение таких программных скоростей, при которых максимальные отклонения лежат в допустимых пределах.
- Определение отклонений от программной скорости по траектории вследствие динамических погрешностей.
- Расчет компенсирующих динамические погрешности поправок на координаты по траектории.
- Определение приемлемых или наилучших законов аппроксимации реальных траекторий кривыми, принадлежащими тому же семейству для реализации вычисленных поправок.
- Окончательный выбор параметрических поправок к программным траекториям, при которых получается достаточная или наилучшая для выбранного класса аппроксимация (в разных вариантах, например, вписанной и описанной окружностей, при односторонних допусках).
- Анализ остаточных погрешностей после введения поправок. В упрошенном варианте блок-схема обобщенного алгоритма вычисления погрешности отработки программной траектории представлена на рисунке1 [1, c 55].
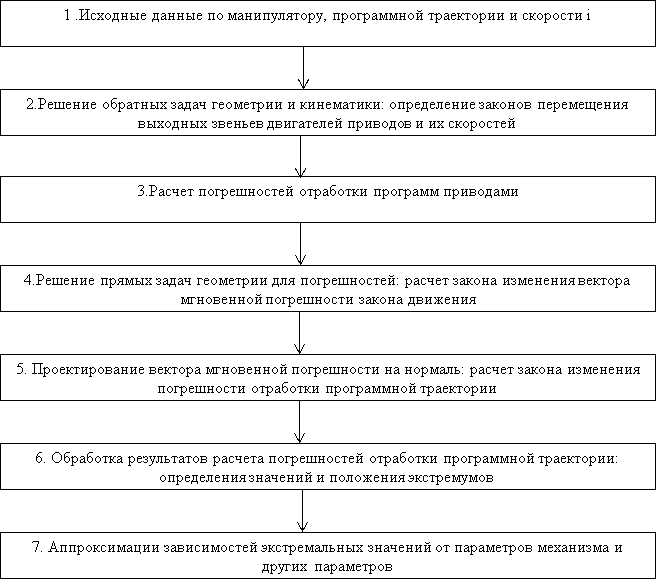
Рис. 1. Блок-схема обобщенного алгоритма вычисления погрешности
Решение обратных задач геометрии и кинематики (заданы траектория движения рабочей точки манипулятора и закон изменения программной скорости, определяются законы движения двигателей приводов) на этапе 2 должно осуществляться точно, в больших углах и в полных диапазонах перемещений.
Для достаточно сложных кинематических схем решение обратной задачи на этапе 2 разбивается на два подэтапа: сначала определяются обобщенные координаты механизма, а затем законы движения выходных звеньев двигателей приводов. На большинстве последующих этапов может быть использована линеаризация, если она дает практическое упрощение вычислительных процедур. При проектировании вектора синхронной погрешности на нормаль необходимо знать направление последней; если программная траектория задается как прямая, окружность или их сопряжение, то одновременно задаются и нормали. Для других, более сложных кривых, тем более пространственных, необходим под этап расчетного определения направления нормали.
На этапе 6 первичной обработки результатов расчетов помимо определения экстремальных значений отклонений может быть предусмотрено определение, например, их положения, среднеквадратичных отклонений и т. п. Возможно также осуществление статистического моделирования при различным образом задаваемых случайных влияющих факторов.
На последнем этапе 7 может осуществляться аппроксимация самих реальных траекторий простыми аналитическими зависимостями, что определяет конструктивные пути построения корректирующих поправок (они рассмотрены подробно далее); аппроксимации могут быть также полезными также для описания зависимостей характеристик остаточных погрешностей (после введения корректирующих поправок) от различных параметров манипулятора и привода.
Погрешность изменяется по дуге контура и может изменять знак. Она будет считаться положительной, если ее вектор направлен от центра кривизны программной траектории, и отрицательной, если направлен к центру кривизны. Если программная траектория — прямая, то выбор положительного направления произволен. Наибольший интерес представляют экстремальные значения погрешности воспроизведения траектории, причем значимость отклонений в одну и другую сторону от программной траектории может быть различной, поэтому их нужно регистрировать раздельно.
Литература:
1. Никифоров C.O., Мархадаев Б. Е. Алгоритм формирования точностных показателей промышленных роботов.// Вестник машиностроения, 2001, № 4,2001.







