1.      Введение и постановка задачи

В настоящее время получили широкое распространение различные корпоративные системы учета класса ERP (enterprise resource planning, корпоративное планирование ресурсов), предназначенные для интеграции данных о функционировании предприятия [2]. Но, как правило, такие системы обладают достаточно скудными возможностями анализа накопленной информации. Одной из актуальных задач является сравнение различных последовательностей данных, например при сравнении множества вариантов бюджетов [4]. Сложность такого сравнения обусловлена большим объемом данных, причем сравнение агрегированных показателей за период не дает точности при оперативном планировании, напротив сравнение последовательностей ежедневных показателей в ручном режиме нецелесообразно.

Другой сложностью является природа исследуемых данных. Их особенностью является наличие резких всплесков, а также небольшие сдвиги относительно друг друга, что делает трудным использование корреляционного анализа. С другой стороны дело осложняется большой протяженностью последовательностей, что при наличии резких всплесков делает трудным использование спектральных методов, из-за сложности выбора гармоник [1]. К тому же, должна достигаться высокая скорость обработки информации и экономия вычислительных ресурсов.

Очевидно, что актуальным является разработка методики сравнения дискретных данных с учетом вышеприведенных требований.

2.      Разработка методики сравнения

Предложенная методика состоит из четырех этапов:

·         кодирование качественных характеристик;

·         дополнение последовательности нулями до длины ;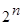

·         вычисление значений векторов 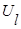 для сравниваемых сигналов;

·         вычисление расстояния 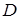 для сравниваемых сигналов.

Первый этап методики необязателен и используется только в случае, если элементами дискретной последовательности являются качественные значения, как например, при использовании KPI (key performance indicators, ключевые показатели эффективности).

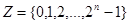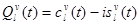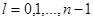Второй этап необходим, так как предложенная базисная комплексная система импульсных функций определяется на множестве , и имеет вид , где  - номер гармоники анализируемого сигнала. 

Третий этап заключается в формировании амплитудно-частотного спектра анализируемой последовательности 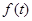 [3], который вычисляется в соответствии с выражением 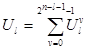, где 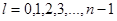. Выражение  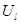представляет собой суперпозицию значений: 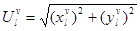, где: 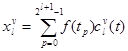, , 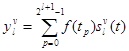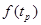- значение анализируемой последовательности в точк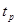е , где 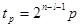. То есть, на каждой гармонике спектр представляет собой суперпозицию значений сигнала умноженного на значения опорных импульсных функций, которые подвергаются сдвигу на значение  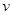подинтервалов внутри каждого интервала. Функци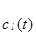и  и 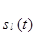 определяются как:  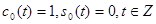для нулевой гармоники 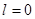. В случае, если  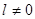и изменяется от 0 до  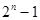с шагом 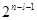, функции записываются как: 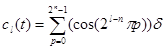,  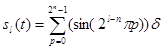     , где .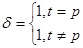

При практической реализации алгоритма, предложено вместо вычисления тригонометрических функций синуса и косинуса использовать матрицу заранее вычисленных значений. Для выражения 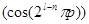 такая матрица записывается как:

,

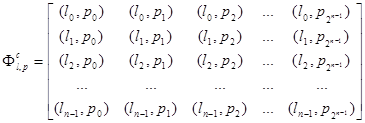Для выражения 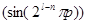 матрица записывается как:

.

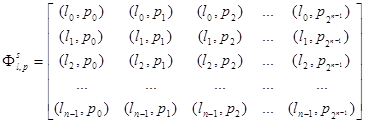Таким образом, импульсные функции запишутся как: , .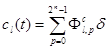

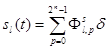Реализация данного подхода позволяет отказаться от вычисления значений тригонометрических функций, что значительно ускоряет процедуру вычисления. Для каждой гармоники множество 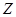 делится на  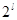интервалов, в каждом из которых происходит сдвиг импульсных функций на  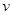подинтервалов. С учетом произведенных изменений спектр  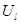запишем как:

.

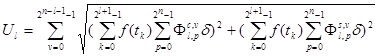Сдвигаемые опорные импульсные функции формируются на основе вспомогательных функци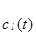й  и 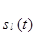, их можно записать как: 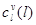и 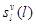. Количество сдвигов можно определить как  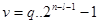, где 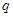 - позиция первого подинтервала, с которого начинается сдвиг.

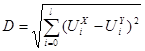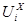Четвертый этап заключается в вычислении евклидова расстояния , где  и 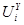 вектора спектров двух последовательностей, описывающих реализации X и Y анализируемых последовательностей соответственно,  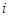- номер гармоники, который соответствует измерению вектора. Сравнивая попарно все исследуемые последовательности, находится 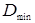, которым определяется наибольшая мера сходства.

3.      Исследование эффективности разработанной методики

Для исследования эффективности был проведен численный эксперимент. Было использовано 30 реализаций значений бюджета затрат на производство в натуральном выражении, характеризующих запланированный выпуск определенного вида продукции.

Все исследованные реализации  имеют одно и то же функциональное назначение и различаются особенностями, которые выражаются в незначительных изменениях фазы и амплитуды, что связано с изменением внешней среды, т.е. при сравнении таких данных должна наблюдаться высокая связь.

Была произведена оценка 435 взаимных сочетаний исследуемых реализаций, которое равно 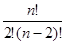, где 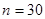- количество исследуемых реализаций. На рисунке 1 изображены значения расстояния  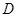для всех сочетаний реализаций, .

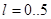Рис.1. Значения расстояния 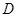 для исследуемых сочетаний реализаций, .

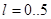На рисунке 2 представлены значения расстояний 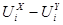 по каждому измерению, где  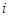- номер измерения. Видно, что на последних гармониках наблюдается больший разброс значений.

Рис.2. Значения расстояний  по измерениям для исследуемых сочетаний реализаций, .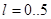

При выборочном сравнении различных сочетаний реализаций было подтверждено, что наибольшие значения 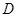 соответствуют наименьшему сходству реализаций.

4.      Выводы

Разработанная методика позволяет сравнивать дискретные данные, используя сжатие в 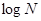 раз. Кроме этого, спектр  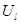инвариантен к сдвигам сигнала и зависит от самых небольших изменений сигнала, что позволяет хорошо выделить структурные особенности данных. Выбранная мера сходства  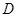позволяет адекватно оценить схожесть данных, причем наименьшим значениям соответствует наибольшее сходство. Указанные преимущества создают предпосылки для разработки практической реализации разработанной методики для использования в различных бизнес-приложениях.

Литература:

1.      Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов: Учеб. Пособие для вузов. - М.: Радио и связь, 1990. – С.123-143.

2.      Рыбников А.И. Система управления предприятием типа ERP. – М.: Азроконсалт, 1999. – 214 с.

3.      Тверетин, А.А. Сравнение конкатенированных данных на основе их спектральных характеристик/ А.А. Тверетин, Л.С. Бекасов // Современные наукоемкие технологии.  – Москва, 2008. - №6. – C. 34-39.

4.      Теплова Т.В. Планирование в финансовом менеджменте. - М.: ГУ ВШЭ, 1998. – С.85 - 91.