Корректный учет нагрузки на валу электрических двигателей является важным условием получения достоверных результатов математического моделирования электрифицированных механизмов. В теории электропривода моменты статического сопротивления механизмов подразделяются на две характерные группы: активные и реактивные. Активные моменты порождаются силами гравитации и упругой деформации и отличаются способностью вызвать движение механизма даже при отключенном двигателе. Реактивные моменты порождаются силами трения и неупругой деформации и всегда проявляют себя как силы, противодействующие движению. Они возникают и в состоянии покоя, как равное противодействие активному усилию двигателя и активной составляющей момента статического сопротивления механизма.
Широко распространенным инструментом решения задач электромеханики является пакет «Matlab – Simulink», где содержится обширная библиотека моделей электрических машин постоянного и переменного тока. Обобщенная структура таких моделей показана на рис. 1.
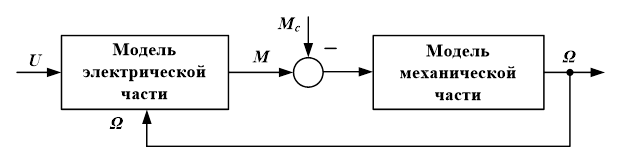 Рис. 1 Обобщенная структура моделей электрических машин
Рис. 1 Обобщенная структура моделей электрических машин
Здесь выделены два основных блока, моделирующих процессы в электромагнитных контурах машины и ее механической части. Момент нагрузки вводится в качестве независимой переменной 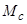 . Такое внешнее воздействие интерпретируется моделью как активный момент статического сопротивления механизма. Отсутствие блока формирования реактивной составляющей момента сопротивления ограничивает область использования подобных моделей в задачах электромеханики. Известны усовершенствованные модели, где порождаемые силами сухого и вязкого трения реактивные моменты статического сопротивления формируются как нелинейные функции скорости [1]. Однако такие модели не учитывают особенностей возникновения и действия сил статического сопротивления механизмов в состоянии покоя.
. Такое внешнее воздействие интерпретируется моделью как активный момент статического сопротивления механизма. Отсутствие блока формирования реактивной составляющей момента сопротивления ограничивает область использования подобных моделей в задачах электромеханики. Известны усовершенствованные модели, где порождаемые силами сухого и вязкого трения реактивные моменты статического сопротивления формируются как нелинейные функции скорости [1]. Однако такие модели не учитывают особенностей возникновения и действия сил статического сопротивления механизмов в состоянии покоя.
Целью данной работы является создание функционального блока, позволяющего моделировать режимы работы электрифицированных механизмов с активными и реактивными моментами статического сопротивления, как при движении, так и при покое.
Теоретическая основа построения такого блока дана в работе [2], где приводится следующая математическая модель вычисления нагрузки на валу двигателя:
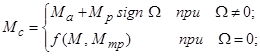 (1)
(1)
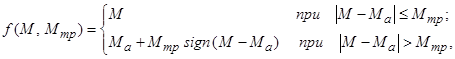
где 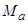 – активный момент статического сопротивления механизма;
– активный момент статического сопротивления механизма;
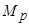 – модуль реактивного момента статического сопротивления, возникающего при движении механизма;
– модуль реактивного момента статического сопротивления, возникающего при движении механизма;
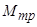 – модуль реактивного момента статического сопротивления при трогании механизма;
– модуль реактивного момента статического сопротивления при трогании механизма;
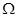 – скорость вращения вала двигателя;
– скорость вращения вала двигателя;
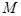 – электромагнитный момент двигателя;
– электромагнитный момент двигателя;
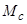 – результирующий момент статического сопротивления механизма, приведенный к валу двигателя.
– результирующий момент статического сопротивления механизма, приведенный к валу двигателя.
Алгоритм функционирования этого блока показан на рис. 2. Правая ветвь алгоритма определяет величину и направление действия реактивной составляющей момента статического сопротивления при движении механизма, как фактора, противодействующего движению. Левая ветвь определяет величину и направление реактивной составляющей момента статического сопротивления в состоянии покоя, как равного противодействия активным усилиям со стороны двигателя и механизма. Средняя ветвь описывает ситуацию, возникающую при трогании механизма, и позволяет учесть различие сил трения в состоянии покоя и движения. Для обеспечения устойчивости численного решения уравнений модели «двигатель-нагрузка» строгие условия идентификации движения (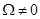 ) и покоя (
) и покоя (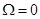 ) из выражений (1) заменены на менее жесткое условие
) из выражений (1) заменены на менее жесткое условие 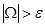 , где
, где 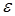 – малая положительная величина.
– малая положительная величина.
Использование данного алгоритма позволяет корректно учесть нелинейные свойства сил трения и неупругой деформации, как при движении, так и при покое, включая условия трогания и остановки механизмов.
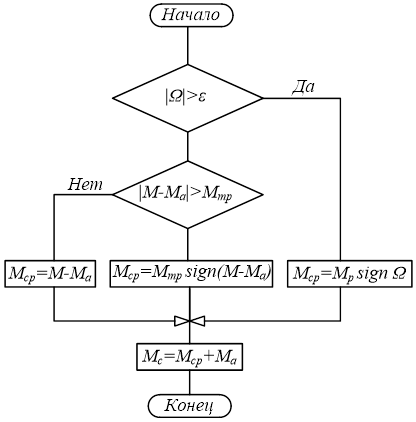
Рис.2 Алгоритм вычисления момента статического сопротивления механизма
Как следует из описанной выше математической модели, момент статического сопротивления механизма представляет собой нелинейную функцию четырех переменных 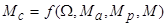 . Для учета сухого и вязкого трения, а также особенностей полезной нагрузки различных механизмов, целесообразно представление модуля реактивной составляющей момента их статического сопротивления, как комбинации постоянной составляющей, линейной, квадратичной и кубической функций скорости:
. Для учета сухого и вязкого трения, а также особенностей полезной нагрузки различных механизмов, целесообразно представление модуля реактивной составляющей момента их статического сопротивления, как комбинации постоянной составляющей, линейной, квадратичной и кубической функций скорости:
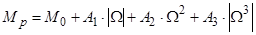 , (2)
, (2)
где 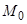 – постоянная составляющая модуля реактивного момента;
– постоянная составляющая модуля реактивного момента;
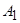 ,
, 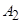 ,
, 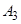 – весовые коэффициенты переменных составляющих модуля реактивного момента сопротивления механизма.
– весовые коэффициенты переменных составляющих модуля реактивного момента сопротивления механизма.
Обобщенная структура модели электрического двигателя с блоком моделирования нагрузки приобретает вид, показанный на рис. 3. В отличие от структуры рис.1 здесь присутствуют связи по электромагнитному моменту и скорости двигателя, необходимые для корректного вычисления реактивной составляющей момента статического сопротивления 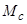 на валу двигателя в блоке модели нагрузки. Модуль реактивной составляющей формируется нелинейным блоком в соответствии с формулой (2).
на валу двигателя в блоке модели нагрузки. Модуль реактивной составляющей формируется нелинейным блоком в соответствии с формулой (2).
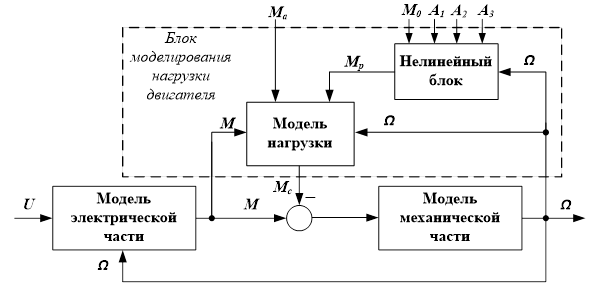
Рис. 3 Обобщенная структура модели электрического двигателя с блоком моделирования нагрузки
В приложение к библиотеке моделей электрических машин пакета «Matlab – Simulink» разработан блок моделирования нагрузки двигателя, структура которого показана на рис. 4. Здесь скорость обозначена как W.

Рис.4 Блок моделирования нагрузки на валу двигателя
В соответствии с алгоритмом вычисления 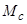 (рис. 2), в модели нагрузки сформированы три субсистемы (Subsystem1, 2, 3), моделирующие три ветви исходного алгоритма. Модели этих субсистем показаны на рис. 5, 6 и 7. Блоки Relay в структурах Subsystem1 и 3 реализуют релейную функцию
(рис. 2), в модели нагрузки сформированы три субсистемы (Subsystem1, 2, 3), моделирующие три ветви исходного алгоритма. Модели этих субсистем показаны на рис. 5, 6 и 7. Блоки Relay в структурах Subsystem1 и 3 реализуют релейную функцию 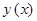 , принимающую значение 1 при
, принимающую значение 1 при 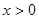 и 0 при
и 0 при 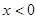 .
.
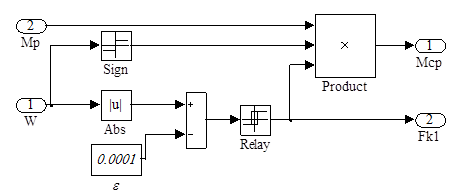
Рис.5 Функциональная модель Subsystem1
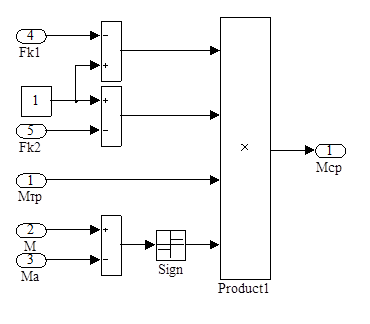
Рис.6 Функциональная модель Subsystem2
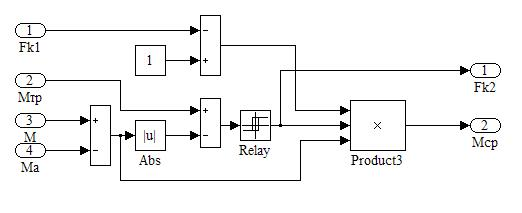
Рис.7 Функциональная модель Subsystem3
Нелинейный блок Subsystem4 позволяет реализовать различные функциональные зависимости модуля реактивного момента от скорости. Соответствующая выражению (2) функциональная модель изображена на рис. 8.
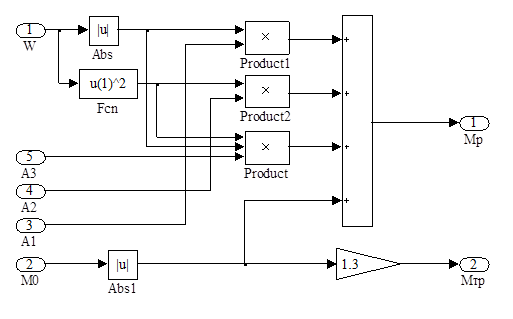
Рис.8 Функциональная модель нелинейного блока
Разработанный блок моделирования нагрузки апробирован в сочетании с моделями различных двигателей постоянного и переменного тока из приложения SimPowerSystems/Machines. В качестве примера использования данного блока на рис. 9 изображена модель электрифицированного механизма с асинхронным короткозамкнутым двигателем, питаемым от управляемого по частоте и амплитуде источника синусоидального напряжения.
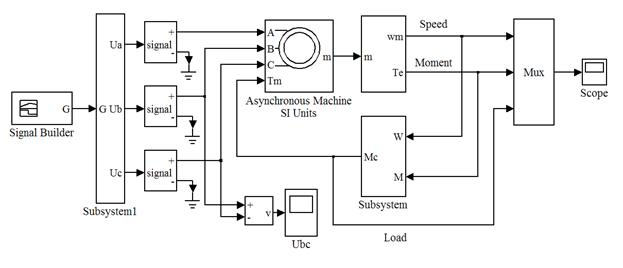
Рис. 9 Модель частотно-регулируемого асинхронного
короткозамкнутого двигателя с блоком моделирования нагрузки
Источник питания двигателя Subsystem1 (структура его модели приведена на рис. 10) обеспечивает пропорциональный закон частотного управления (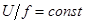 ) и линейное изменение частоты и амплитуды напряжения на зажимах двигателя в режимах пуска, торможения и реверса.
) и линейное изменение частоты и амплитуды напряжения на зажимах двигателя в режимах пуска, торможения и реверса.
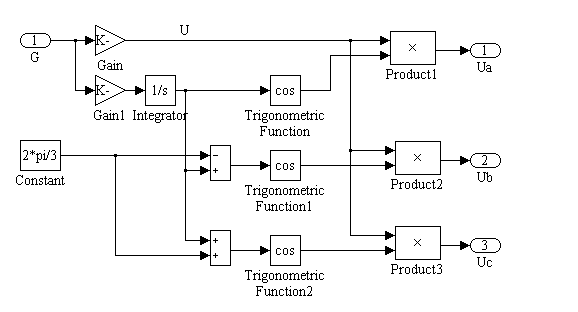
Рис.10 Функциональная модель источника питания двигателя
Асинхронный короткозамкнутый двигатель (Asynchronous Mashine) имеет следующие паспортные данные и параметры схемы замещения: 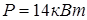 ,
, 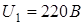 ,
, 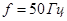 ,
, 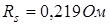 ,
, 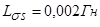 ,
, 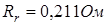 ,
, 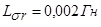 ,
, 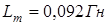 ,
, 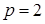 . Приведенный к валу электродвигателя суммарный момент инерции механической системы
. Приведенный к валу электродвигателя суммарный момент инерции механической системы 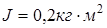 . Механизм характеризуется переменным реактивным моментом, включающим постоянную и квадратичную составляющие зависимости момента сопротивления от скорости. Момент трогания превышает постоянную составляющую на 30%. Принятые при моделировании численные значения параметров нагрузки
. Механизм характеризуется переменным реактивным моментом, включающим постоянную и квадратичную составляющие зависимости момента сопротивления от скорости. Момент трогания превышает постоянную составляющую на 30%. Принятые при моделировании численные значения параметров нагрузки 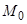 ,
, 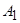 ,
, 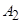 ,
, 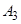 и величины ε в блоке моделирования нагрузки Subsystem (Рис. 9) показаны на рис. 4 и 5.
и величины ε в блоке моделирования нагрузки Subsystem (Рис. 9) показаны на рис. 4 и 5.
На рис. 10 приведены результаты моделирования процессов частотного пуска, установившегося движения и реверса механизма. Графики изменения во времени величин скорости 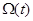 , электромагнитного момента
, электромагнитного момента 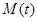 и момента статического сопротивления на валу двигателя
и момента статического сопротивления на валу двигателя 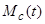 представлены в физических единицах. Как видно, модель адекватно воспроизводит соответствующие реалиям люфты в графиках скорости на начальной стадии пуска и при реверсе, пики момента статического сопротивления при троганиях механизма, а также изменения момента нагрузки
представлены в физических единицах. Как видно, модель адекватно воспроизводит соответствующие реалиям люфты в графиках скорости на начальной стадии пуска и при реверсе, пики момента статического сопротивления при троганиях механизма, а также изменения момента нагрузки 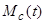 при изменении скорости. Колебания момента
при изменении скорости. Колебания момента 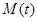 обусловлены электромагнитными переходными процессами в двигателе.
обусловлены электромагнитными переходными процессами в двигателе.
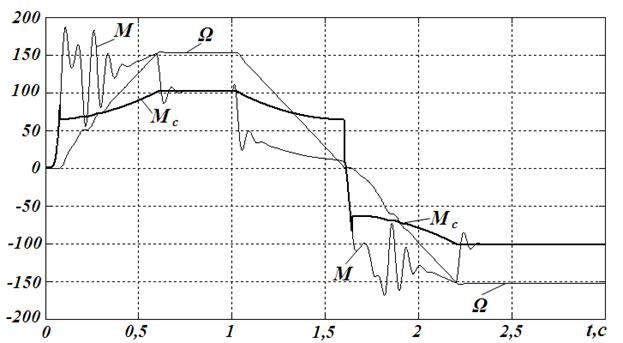
Рис.10 Временная диаграмма пуска, установившегося движения
и реверса электрифицированного механизма с асинхронным короткозамкнутым двигателем
Результаты апробации подтвердили возможность моделирования режимов работы электрифицированных механизмов с различными двигателями и механизмами с активными и реактивными моментами статического сопротивления.
Литература
1. Герман-Галкин С.Г. Matlab & Simulink. Проектирование мехатронных систем на ПК. [Текст] / Спб.: КОРОНА-Век, 2008. – 368 с., ил.
2. Шрейнер Р. Т. Системы подчиненного регулирования электроприводов. [Текст] / Р. Т. Шрейнер. Екатеринбург: Изд-во ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. 279 с.







