Для установления закономерностей каких-либо явлений проводятся экспериментальные исследования, в ходе которых измеряют значение тех или иных физико-химических величин. При проведении любого эксперимента используются приборы различной степени точности. Поэтому результаты любого измерения всегда содержат ошибки и погрешности.

Как правило, при решении прикладных задач необходимо определить точечные и интервальные оценки параметров функций известного вида по полученным экспериментальным данным. В этом случае применяют метод центра неопределенности (МЦН) [1].

При небольшом числе измерений достаточно точные модели позволяет получить метод интервальной оценки параметров трехпараметрического полинома, учитывающий априорную информацию об ошибках измерений непосредственно при расчетах.

Задача принадлежит к классу аппроксимации с целью построения одной общей кривой, проходящей через все заданные точки. Существует два случая:

·         Аппроксимирующая кривая проходит через точки заданной функции в узлах

·         Кривая может не проходить через точки, заданные таблицей, но отклонение от них минимально.

В обоих случаях пытаются минимизировать отклонение. Трудность заключается в том, что значения одной из координат точек заданы в виде интервалов. Чтобы обойти подобное затруднение используют метод центра неопределенностей, где фигурой, оценивающей разброс параметров аппроксимирующих функций, является эллипсоид.

Рассмотрим задачу построения зависимости вида 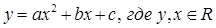 с интервальными значениями y.

Пусть в результате m измерений получены экспериментальные данные, содержащие точные значения входных и интервальные значения выходных переменных:

,

,

........................

.

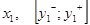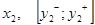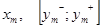Ограничения входных и выходных данных:

1. ;

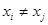2. ;

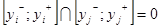3. Данные должны подчиняться определенному закону, а не быть произвольными.

Согласно принципам интервально-статистического анализа запишем систему неравенств:

,.

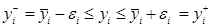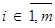Каждое двойное неравенство представляет собой область, ограниченную двумя параллельными плоскостями в декартовой трехмерной системе координат.

Таким образом, искомая область неопределенности заключена в пересечении данных плоскостей и представляет из себя шестигранник. Для того, чтобы получить грубое приближение, нужно найти пересечения для всех троек непараллельных плоскостей путем решения восьми систем линейных уравнений с тремя переменными (для первых трех уравнений):

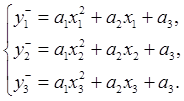
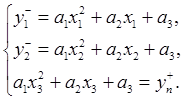
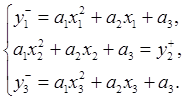
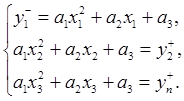
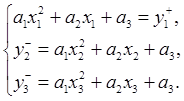
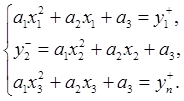
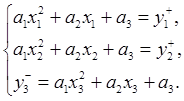
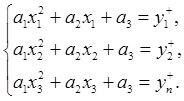
Решив каждую из этих систем, получим координаты соответствующей вершины. Обозначим для удобства искомые переменные как a,b,c, а коэффициенты как k_ij. Тогда система запишется в виде:

 

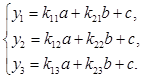
В результате преобразований получим оценки для a, b, c:

;

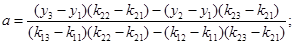
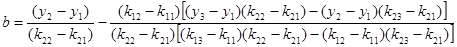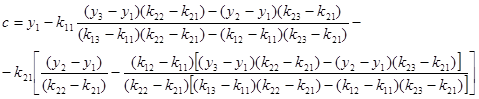
Далее зная координаты точек, можно построить эллипсоид, описанный вокруг шестигранника, который будет начальной грубой оценкой. Так как шестигранник образован парами параллельных плоскостей, то он является параллелепипедом. Его центр находится на пересечении диагоналей, центр эллипсоида будет совпадать с центром параллелепипеда.

Для того чтобы натянуть на параллелепипед эллипсоид минимального объема, найдем матрицу аффинного преобразования с помощью которой данный параллелепипед получается из куба. Выберем новую систему координат, оси которой будут начинаться в центре параллелепипеда и заканчиваться на центрах трех смежных граней. Обозначим 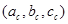 - координаты центра параллелепипеда и эллипсоида. 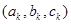, где k=1..3, — координаты центров трех смежных граней. Переход от одних  координат к другим в матричном виде запишется так: 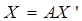, где X – старые координаты, X' – новые, А – матрица перехода. В наших обозначениях, матрица перехода имеет вид:

 

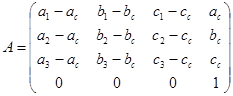
В новых координатах эллипсоид представляет из себя сферу. При подстановке в формулу сферы координат X'=A^-1X, получим явную формулу эллипсоида. Таким образом, получили грубую оценку трехпараметрического множества неопределенности при помощи эллипсоида.

При наличии дополнительных экспериментальных данных, зная первоначальное приближение, необходимо провести уточнение эллипсоида неопределенности. Данные нового измерения в пространстве представляют из себя полосу, ограниченную двумя параллельными плоскостями, которые при пересечении с эллипсоидом грубой оценки дадут новое множество неопределенности. Опишем его новым эллипсоидом минимального объема.

Пусть в R³ заданы эллипсоид E и полоса R, определяемые неравенствами:

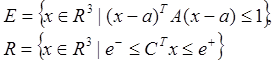
Построим эллипсоид минимального объема, содержащий тело 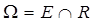. Множество R можно задать следующим образом: 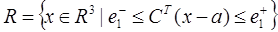, если обозначить

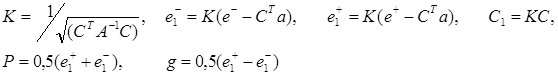
В силу новых обозначений запишем уравнение множества R в эквивалентном виде:

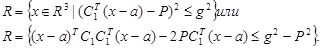
Имеет место нормировочное соотношение: .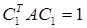

Пусть вещественные числа ω и u удовлетворяют условиям:

.

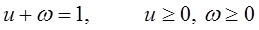Комбинируя неравенства для эллипсоида и полосы получим однопараметрическое семейство эллипсоидов, содержащих тело :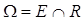

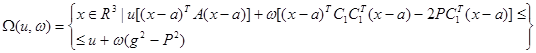
Обозначим 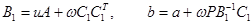. Тогда уравнение примет вид:

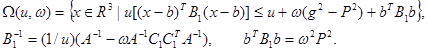
Обозначив 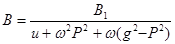, получим выражение для однопараметрического семейства эллипсоидов:

.

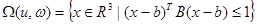Объем такого эллипсоида определяется соотношением:

.

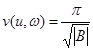Определитель матрицы В пропорционален определителю матрицы A и определяется по формуле:

.

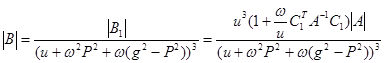Коэффициент пропорциональности зависит от u. Обозначим этот коэффициент:

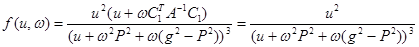
Далее найдем максимум функции 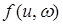. Для этого введем новую функцию  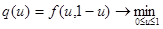, прологарифмируем ее:

.

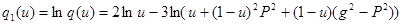Функции q(u) и q₁(u) достигают максимума в одной точке. Исследуя на экстремум функцию q₁(u), получим два корня:

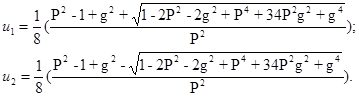
Подставляя найденное значение в соответствующие выражения, получаем матрицу коэффициентов B, и объем искомого эллипсоида.

 

Литература

1.    Белов, В.М. Оценивание параметров эмпирических зависимостей методом центра неопределенности/ В.М. Белов [и др]. – Новосибирск: Наука,2001. – 176 с.