Для улучшения качественных показателей технологического процесса обработки почвы на вырубках предложена новая конструкция лесного дискового плуга с комбинированным рабочим органом (рисунок 1) [1].
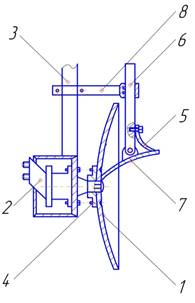
Рисунок 1 – Корпус лесного дискового плуга
Сферический диск 1 приводится во вращение гидромотором 2, к рабочей поверхности диска посредством листовой пружины 5 прижато крыло отвала 7, которое шарнирно соединено с кронштейном 6, закрепленным на консоли 8. Пласт почвы, поднимаясь по диску, скользит по отвалу и укладывается вдоль борозды сплошной лентой.
С целью обоснования основных параметров рабочего органа плуга была разработана математическая модель [2] .
Плуг в модели представляет собой комбинацию двух геометрических поверхностей: сегментного участка сферической поверхности (дисковый корпус) и участка плоскости (отвал) (рисунок 2 а).
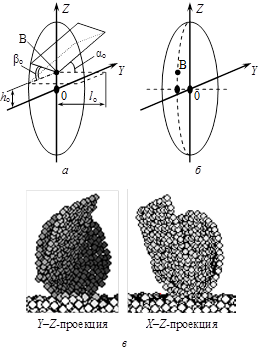
Рисунок 2 – Дисковый корпус с отвалом в модели: а – параметры, задающие положение отвала; б – реальное положение точки B на сферическом диске; в – изображение плуга с отвалом, выводимое на экран компьютера
Основными параметрами, задающими положение отвала в виде участка плоскости, являются поперечный αо и продольный βо углы установки плоскости и положение hо точки B стыковки отвала и сферического диска. Для изучения влияния указанных параметров на эффективность обработки почвы на основе разработанной математической модели было проведено три серии компьютерных экспериментов.
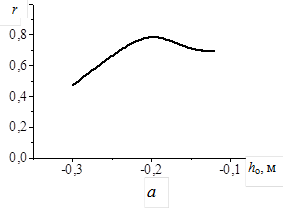
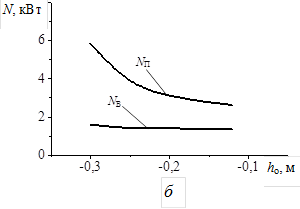
Рисунок 3 – Влияние вертикального положения отвала hо на качественный (а) и энергетические (б) показатели обработки почвы: NП – мощность, затрачиваемая на поступательное движение плуга; NВ – мощность, затрачиваемая на вращение диска плуга.
Вертикальное положение отвала hо изменяли от –0,30 до –0,10 м с шагом 0,05 м (рисунок 3). На графике зависимости коэффициента оборачиваемости пласта от высоты установки отвала r(hо) наблюдается четко выраженный максимум при значении hо вблизи –0,20 м. При слишком высоком расположении отвала вырезаемый диском пласт, поднимаясь по диску, срывается с него, не доходя до отвала, поэтому при больших hо оборачиваемость пласта невысока. При слишком низком расположении отвал "прижимает" формирующийся пласт, не дает ему подниматься по диску, поэтому оборачиваемость пласта r при малых hо также падает.
С уменьшением hо мощность поступательного движения резко возрастает. Это обусловлено тем, что мощность начинает расходоваться на "прижатие" пласта и на протягивание отвала в почве. Вследствие последнего эффекта деформируется профиль борозды (рисунок 4, вверху).
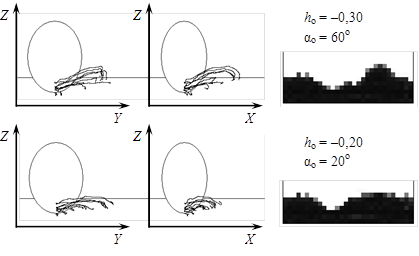
Рисунок 4 – Форма борозды при различных параметрах установки отвала
Слишком низкое расположение отвала hо (вверху) или слишком малый поперечный угол наклона αо (внизу) приводят к "прижиманию" пласта и нарушению формы борозды
Таким образом, оптимальное положение отвала, обеспечивающее высокую оборачиваемость пласта и низкие энергозатраты составляет hо = –0,20 м.
Следующая серия компьютерных экспериментов проводилась с изменением угла αо наклона отвала от 20о до 70о с шагом 10о (рисунок 5).
В целом ход зависимостей NП(αо), NВ(αо) и r(αо) аналогичен предыдущему случаю, так как изменение угла наклона отвала при фиксированной точке B стыковки его с диском равносильно изменению расстояния от отвала до уровня почвы. При αо = 60о наблюдается максимум коэффициента оборачиваемости r. Кроме того, зависимость поперечного смещения пласта d(αо) также имеет максимум при αо = 40о. При увеличении поперечного угла отвала от 40о его плоскость удаляется от почвы, и он оказывает меньшее влияние на смещение пласта. С другой стороны, при уменьшении αо от 40о отвал все сильнее входит в почву, разрушает и перемешивает образовавшийся пласт, и эффективность смещения пласта резко снижается (рисунок 5 б).

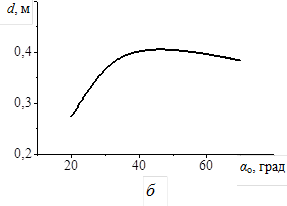

Рисунок 5 – Влияние угла αо наклона отвала на качественные (а, б) и энергетические (в) показатели обработки почвы: NП – мощность, затрачиваемая на поступательное движение плуга; NВ – мощность, затрачиваемая на вращение диска плуга.
Следует отметить, что при малых углах αо достигаются практически нулевые значения коэффициента r (рисунок 5 а). Это означает, что пласт в этом случае смещается, не переворачиваясь.
В следущей серии компьютерных экспериментовов изменялся продольный угол βо установки отвала от –30о до –10о с шагом 5о (рисунок 6).
Как видно из графиков, NВ и r практически не зависят от βо. Отсутствие зависимости, по-видимому, обусловлено тем, что почвенная масса поступает на отвал снизу, поднимаясь по сферическому диску. Поэтому основной эффект переворота пласта оказывает установка отвала под некоторым поперечным углом αо, а не βо. Угол же βо оказывал бы влияние, если бы почвенная масса поступала преимущественно в продольном направлении.
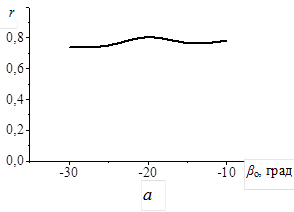
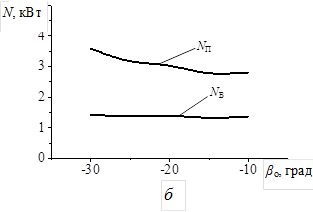
Рисунок 6 – Влияние угла βо наклона отвала на качественный (а) и энергетические (б) показатели. NП – мощность, затрачиваемая на поступательное движение плуга; NВ – мощность, затрачиваемая на вращение диска плуга.
Некоторый рост NП при уменьшении βо, как и ранее, можно объяснить тем, что плоскость отвала начинает "задевать" необработанную почву.
Построенные для αо = 60о графики NП(βо), NВ(βо) и r(βо) демонстрируют практически полное отсутствие функциональной зависимости. Однако при малых значениях αо, например, при αо = 30о, перечисленные зависимости очень сильны. Это будет покзано ниже в ходе оптимизации основных параметров плуга.
Таким образом, на эффективность функционирования отвала наибольшее влияние оказывают параметры hо и αо. Кроме того, при установке отвала необходимо обеспечить некоторый зазор между отвалом и уровнем почвы.
Форма и положение отвала дискового плуга оказывают существенное влияние на эффективность обработки почвы. В частности, важно знать, каковы должны быть углы αo и βo установки основной плоскости отвала, чтобы энергозатраты на обработку почвы были низкими, а качество обработки высоким. Это позволит сформулировать рекомендации по оснащению дискового плуга отвалом.
Параметрическая оптимизация сложных систем в общем случае сводится к задаче поиска экстремума функции нескольких переменных. При этом необходимо определить такие области изменения входных параметров, при которых параметры материала удовлетворяют некоторому принятому критерию, либо нескольким частным критериям [3]. Для того чтобы критерий оптимизации всесторонне характеризовал изучаемую систему, его обычно составляют в виде линейной комбинации с соответствующими весовыми коэффициентами нескольких частных критериев оптимизации ki, представляющих собой экономические или качественные показатели [4]. В данном случае в качестве частных критериев целесообразно использовать затрачиваемую на поступательное движение и на вращение мощность N(αo, βo) и коэффициент оборачиваемости r(αo, βo).
Таким образом, необходимо решить следующую задачу оптимизации: одновременно минимизировать функцию N(αo, βo) и максимизировать функцию r(αo, βo) путем согласованного подбора факторов αo и βo.
В процессе оптимизации углов установки отвала использовали те же интервалы варьирования факторов, что и на этапе систематических исследований: поперечный угол αo варьировали от 30 до 70 градусов с шагом 10 градусов, продольный угол βo варьировали от –30 до –10 градусов с шагом 5 градусов. При этом в каждой из 25-ти точек (αoi, βoi) проводили по два компьютерных эксперимента с последующим усреднением получающихся результатов Ni и ri. Далее, для сглаживания случайных ошибок, полученные в табличном виде зависимости N(αo, βo) и r(αo, βo) аппроксимировали полиномиальной поверхностью второго порядка (рисунок 6), по которой и производили оптимизацию [5].
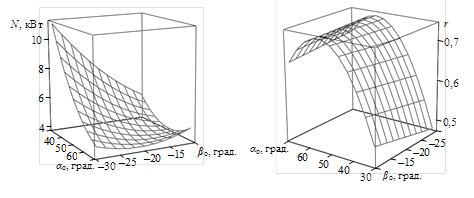
Рисунок 7 – Поверхности отклика N(αо, βо), r(αо, βо), N(hо, ω), r(hо, ω): слева – результаты компьютерного эксперимента, справа – аппроксимирующие поверхности
Важным преимуществом двухфакторной оптимизации является возможность графически изобразить поверхности отклика и провести их визуальный анализ (рисунок 7). Анализируя каждую из поверхностей отклика, представленную с помощью линий уровня, можно условно разделить факторное пространство на две области: благоприятную (заштрихована на рисунке 8), в которой частный критерий оптимизации принимает искомые минимальное или максимальное значения, и неблагоприятную. В качестве границы между благоприятной и неблагоприятной областью экспертным путем выбирается некоторая линия уровня. При этом необходимо учитывать ряд требований [6]:
- благоприятная область должна содержать наиболее экстремальные (максимальные или минимальные) значения критерия;
- в благоприятной области критерий, по возможности, должен быть более-менее постоянным;
- благоприятная область должна занимать значительную долю факторного пространства (20–40 %).
В данном случае в качестве границы были выбраны изолиния мощности N = 4 кВт, изолиния коэффициента оборачиваемости r = 0,75.
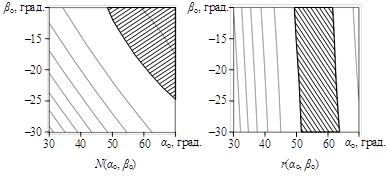
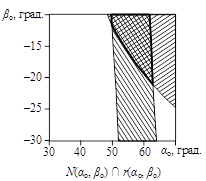
Рисунок 8 – Благоприятные области факторного пространства (заштрихованы) на поверхностях отклика
Совместный учет конфигурации благоприятных областей в факторных пространствах N(αo, βo) и r(αo, βo) позволил сделать вывод, что оптимальные значения параметров αo и βo заключены в области приблизительно треугольной формы, изображенной на рисунке 8 в. Оптимальные диапазоны факторов составляют 50О < αo < 65О; –20О < βo < –10º.
Тот факт, что оптимальная область занимает значительную площадь факторного пространства, косвенно свидетельствует о малой чувствительности предлагаемой конструкции к условиям эксплуатации и поэтому гарантирует стабильную работу предлагаемой конструкции.
Выводы
1. Разработана имитационная компьютерная модель взаимодействия дискового плуга с почвой на основе метода конечных элементов. Модель позволяет по заданным параметрам плуга, почвы и условий эксплуатации определить энергетические затраты и качество обработки почвы.
2. Оснащение плуга отвалом приводит к существенному улучшению качества обработки почвы: на 14 % увеличивается оборачиваемость пласта, уменьшается фрагментация пласта, борозда имеет более четкую округлую форму, а вырезанный пласт отбрасывается дальше в поперечном направлении, что уменьшает вероятность ссыпания пласта обратно в борозду. При этом затраты мощности увеличиваются всего на 8,6 %.
3. При выборе конфигурации отвала и его расположении по отношению к диску необходимо руководствоваться следующими требованиями:
- отвал в совокупности со сферической поверхностью диска должен создавать винтовую поверхность;
- вырезаемый пласт, поднимаясь по вращающемуся диску, должен достигать отвала ранее, чем он сорвался бы с диска;
- отвал необходимо устанавливать с некоторым зазором от уровня почвы (примерно 5 см).
4. Высоту расположения отвала (по отношению к оси диска) необходимо выбирать в зависимости от глубины обработки почвы. При глубине обработки a = 15 см и принятой конфигурации отвала оптимальное положение точки B на 20 см ниже оси диска.
5. Оптимальные диапазоны углов установки отвала αо и βо, обеспечивающие одновременно минимальные энергозатраты и высокую оборачиваемость пласта, следующие: 50О < αo < 65О; –20О < βo < –10О.
6. Согласованная оптимизация высоты расположения отвала ho по условиям минимума энергозатрат и высокой оборачиваемости пласта позволила определить оптимальные диапазоны факторов: –22 см < hо < –13 см.
Литература
1. Пат. 64843 РФ, МПК А 01 В 9 / 00. Дисковый корпус плуга [Текст] / П. И. Попиков, П. Э. Гончаров, С. В. Дорохин, В. Н. Коротких ; заявитель и патентообладатель ВГЛТА. – № 2007108331/22; заявл. 05.03.2007; опубл. 27.07.2007. Бюл. № 21. – 3 с.
2. Коротких, В. Н. Математическая модель взаимодействия сферического диска с приводом от гидромотора лесного плуга с почвой [Текст] / В. Н. Коротких // Вестник КрасГАУ. − 2008. − № 6. − С. 129-135.
3. Мельников С.В., Алешкин В.Р., Рощин П.М. Планирование эксперимента в исследованиях сельскохозяйственных процессов. - 2-е изд., перераб. и доп. - Л.: Колос, 1980. - 168 с.
4. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. - М.: Наука, 1976. - 279 с.
5. Румшиский Л.З. Математическая обработка результатов эксперимента. – М.: Наука, 1971. – 192 с.
6. Дегтярев Ю.И. Методы оптимизации: Учеб. пособие для вузов. - М.: Сов. радио, 1980. - 272 с.







