Рассмотрена задача интерполяции функции, заданной на регулярной сетке, для случая большого числа переменных. Предложена формула для интерполирующей функции в случае произвольного числа переменных n. Исследованы свойства интерполирующей функции и показано ее соответствие случаю одномерной и двумерной интерполяции. Приведен пример использования предложенного алгоритма интерполяции к определению скосов потока в промежуточных точках и режимах обтекания.
Ключевые слова: многомерная интерполяция, регулярная сетка, сеточная вектор-функция, свойства интерполирующей функции.
The problem of interpolation function given on a regular grid, for the case of a large number of variables is considered. A formula for interpolation function in the case of an arbitrary number of variables n is given. The properties of the interpolating function are investigated and show its compliance with the occasion of the one-dimensional and two-dimensional interpolation. An example of using the proposed interpolation algorithm to determine downwash at intermediate points and flow regimes is given.
Keywords: multivariate interpolation, a regular grid, vector function, the properties of the interpolation function
Введение. Необходимость использования многомерной интерполяции часто возникает в реальных приложениях. Достаточно упомянуть задачу масштабирования цифровых изображений или в задачи, возникающие в электронной картографии.
У автора такая потребность возникла при создании математической модели, описывающей поле скоростей неоднородного потока, полученное в экспериментальных исследованиях физической модели при продувке ее в аэродинамической трубе. В результате эксперимента определяются величины продольного e и бокового s скосов потока лишь в точках прямоугольной пространственной сетки координат и для некоторых режимов испытаний, характеризуемых дискретным набором углов атаки a модели и чисел Маха M набегающего потока.
Из необходимости вычисления параметров потока e и s в произвольной пространственной точке R = (x,y,z) и для произвольного режима обтекания, характеризуемого числами a иM, возникает задача интерполяции сеточной функции многих переменных. Число компонент m вектор-функции F в данном случае равно двум: e, s, число переменных nравно пяти: x, y ,z, a, M.
Сложность задачи состоит в большом числе переменных, по которым необходимо осуществлять интерполяцию.
Для случая одной переменной разработаны множество методов интерполяции, основанных, например, на использовании многочленов Лагранжа [1]-[3], сплайн-функций [5]-[6], кривых Безье и B-сплайнов [7].
Задача многомерной, в частности, двумерной интерполяции рассматривались в работах [4], [8], [9], там же отмечены трудности, возникающие при решении этой задачи [4, С. 47], [8, С. 181].
Метод, сводящий многомерную интерполяцию к последовательности одномерных, возможен, но трудоемкость его реализации резко возрастает с увеличением числа переменных n = 2, 3, 4 и т.д.
Предлагаемый подход к многомерной интерполяции сеточной вектор-функции, заданной на регулярной сетке узлов, одинаково пригоден для любого числа аргументов.
Формула и алгоритм интерполяции. Рассмотрим задачу интерполяции в линейной постановке для случая произвольного числа переменных n и произвольного числа компонент m вектор-функции.
Пусть в n–мерной области Dn Ì En введена регулярная пространственная сетка узлов C
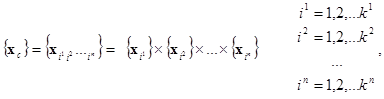
являющаяся декартовым произведением одномерных сеток Cj и разбивающая область Dn на элементарные ячейки 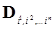 . Индекс вверху j означает номер координаты, индекс внизу i означает номер узла.
. Индекс вверху j означает номер координаты, индекс внизу i означает номер узла.
В области Dn определена сеточная вектор-функция Fc(xc) с размерностью m, т.е. заданы значения m компонент функции Fc в узлах xc:
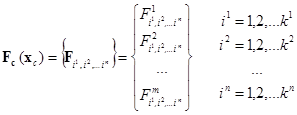
Необходимо построить интерполяционную функцию F(x), где x = {x1, x2,…, xn} – вектор аргументов, которая в узлах сетки совпадала бы с сеточной функцией, т.е. удовлетворяла бы равенству:
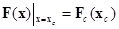 .
.
Для построения такой функции используем локальный подход: значение функции в точке x, попадающее в ячейку сетки 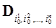 , т.е. удовлетворяющие условиям:
, т.е. удовлетворяющие условиям:
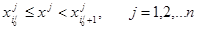 , (1)
, (1)
определяется значениями сеточной функции Fc(xc) только в вершинах этой ячейки.
Таким образом, сначала необходимо определить в какую элементарную ячейку 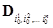 попадает точка x, затем уже определить значение интерполяционной функции F по заданным значениям сеточной функции в вершинах ячейки. При небольшом числе узлов проще и быстрее использовать прямой перебор узловых точек до выполнения условий (1).
попадает точка x, затем уже определить значение интерполяционной функции F по заданным значениям сеточной функции в вершинах ячейки. При небольшом числе узлов проще и быстрее использовать прямой перебор узловых точек до выполнения условий (1).
Образуем величины
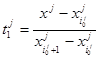
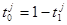 .
.
Требуемую интерполирующую функцию F(x), определенную для каждой ячейки сетки 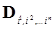 , построим следующим образом:
, построим следующим образом:
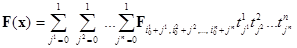 (2)
(2)
Легко заметить, что построенная таким образом функция F(x) в области Dn, являющейся объединением ячеек 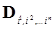 , обладает следующими свойствами.
, обладает следующими свойствами.
1. Функция определена во всей области Dn.
2. Функция совпадает с сеточной функцией Fc(xc) в узлах сетки C.
3. Функция непрерывна во всей области Dn.
4.Функция является кусочно-полиноминальной степени n относительно совокупности переменных x1, x2,…xn.
5. Функция является кусочно-дифференцируемой, разрывы частных производных имеют место лишь на границах ячеек.
6. Функция линейна на границах каждой ячейки.
Предложенный алгоритм интерполяции сеточной вектор-функции многих переменных является обобщением кусочно-линейной интерполяции функции одной переменной, а общая формула (2) в случае, когда имеется зависимость только одной функции от одной переменной (m = 1, n = 1), переходит в обычную формулу линейной интерполяции.
Выпишем явные формулы для одномерной, двумерной, трехмерной интерполяции, записав выражения для относительных координат t1, t2, t3 и формулу (2) для конкретных значений числа аргументов n.
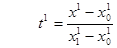 ,
, 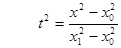 ,
, 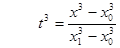 .
.
n = 1: F = F0 (1–t1) + F1 t1 (3)
n = 2: F = F00(1–t1)(1–t2) + F10 t1(1–t2) + F01(1–t1)t2 + F11t1t2 (4)
n = 3: F = F000(1–t1)(1–t2)(1–t3)+ F100t1(1–t2)(1–t3)+ F010(1–t1)t2(1–t3)+ F110t1t2(1– t3)+
+ F001(1–t1)(1–t2)t3+ F101t1(1–t2)t3 + F011(1–t1)t2t3 + F111t1t2t3
На рис. 1 показана иллюстрация предложенного алгоритма интерполяции для случая функции двух переменных.
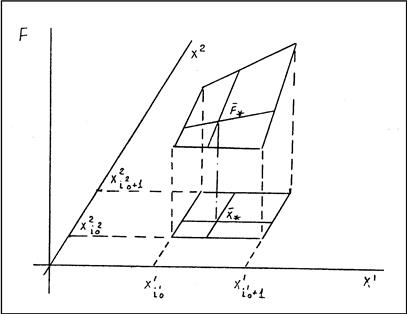
Рис.1 Схема интерполяции для n = 2
Формулы (3), (4) для интерполирующей функции для случая одномерной (n = 1) и двумерной (n = 1) интерполяции соответствуют формулам, приведенным в [10, С. 60]
Из формулы (2) видно, что число слагаемых N экспоненциально увеличивается с увеличением числа аргументов n. Формула (2) содержит n знаков суммирования по индексам переменных, каждый их которых принимает два значения. В соответствии с этим число слагаемых N в формуле (2) для интерполяционной функции связано с числом переменных n формулой
N = 2n.
Так, например, для вычисления интерполирующей функции для случая 10 переменных необходимо использовать более 1000 слагаемых (2n = 1024). Но вовсе необязательно использовать в этом случае явное выражение для интерполяционной функции вида (3) или (4), при написании которой для больших n можно легко ошибиться. При составлении программ, реализующих алгоритм интерполяции, достаточно использовать общую формулу (2) и n вложенных циклов, использующих переменные jk, k = 1,2,…, n. Кроме того, при вычислении всех m компонент вектор-функции F(x) в точке x можно использовать один раз вычисленное значение векторов относительных координат 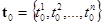 и
и 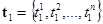 .
.
Пример использования. Описанный алгоритм многомерной интерполяции использован для определения скосов потока e и s в заданной точке R = (x,y,z) и для заданного режима обтекания, характеризуемого параметрами a и M.
В качестве примера на рис. 2 приведены величины скоса потока e для узловых и промежуточных значений аргументов при числе M = 0.6 .
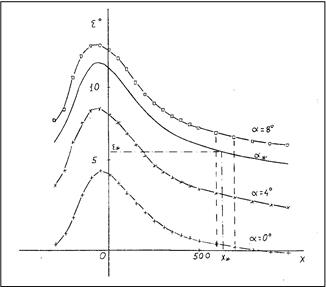
Рис.2 Зависимости скоса потока e для узловых и промежуточных значений x и углов атаки a.
Заключение. В рамках локального подхода предложена формула для интерполяции многомерной сеточной функции для произвольного числа переменных n, в явном виде выражающая ее значения и, соответственно, не требующая решения каких-либо уравнений. Интерполирующая функция обладает рядом необходимых свойств и может быть использована для задач интерполяции в различных приложениях.
Литература:
1. Р.В. Хемминг Численные методы для научных работников и инженеров М. Физматлит, 1972. – 400 c.
2. Б.П. Демидович, И.А. Марон Основы вычислительной математики. – М.: Наука, 1976.
3. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков Численные методы. – М.: Наука, 1987.
4. Н.Н. Калиткин Численные методы. – М.: Наука, 1978– 512 c.
5. Алберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и ее приложения. – М.: Мир, 1972. – 318 c.
6. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. – М.: Наука, 1980. – 352 c.
7. Компьютерная геометрия: Учеб. пособие для студ. вузов. Н.Н. Голованов, Д.П. Ильютко, Г.В. Носовский и др. – М.: Изд. центр “Академия”, 2006 – 312 c.
8. И.С. Березин, Н.П. Жидков Методы вычислений. Т. 1 – М.: Физматлит, 1962. – 464 с.
9. Г.И. Марчук Методы вычислительной математики. – М.: Наука, 1989.
10. Математика и САПР: В 2-х кн. Кн.1. Пер. с франц. / Шенен П., Коснар М., Гардан И. и др. – М.: Мир, 1988. – 204 с.







