В статье описан пример реализации алгоритма Левенштейна на языке  PL/SQL для устранения опечаток в записях баз данных.

Ключевые слова 

Сравнение строк; база данных; редакционное расстояние; расстояние Левенштейна; дистанция редактирования; алгоритм Левенштейна; поиск данных; устранение опечаток.

The example of Levenstein algorithm software realization by PL/SQL language tools for misprint elimination in databases is described in the article.

Keyword

String matching; database; edit distance; Levenstein distance; distance of edit;  Levenstein algorithm; data search; misprint elimination.

Введение

Расстояние Левенштейна (также известное как редакционное расстояние или дистанция редактирования) в теории информации и компьютерной лингвистике – мера различия двух последовательностей символов (строк) относительно минимального количества операций вставки, удаления и замены, необходимых для перевода одной строки в другую [1]. Для одинаковых строк расстояние редактирования равно нулю.

В 1965 году советский математик Владимир Иосифович Левенштейн разработал алгоритм, который позволяет оценить, насколько похожа одна строка на другую. Алгоритм Левенштейна[1] дает возможность получить именно численную оценку похожести строк.

Основная идея алгоритма состоит в том, чтобы посчитать минимальное количество операций удаления, вставки и замены, которые необходимо сделать над одной из строк, чтобы получить вторую.

В настоящее время алгоритм Левенштейна активно применяется в различных программных продуктах, в том числе грамматических приложениях, таких как в MS Office или подобных для решения следующих прикладных задач:

1.                 В поисковых системах для нахождения объектов или записей по имени.

2.                 В базах данных при поиске с неполно-заданным или неточно-заданным именем.

3.                 Для исправления ошибок при вводе текста.

4.                 Для исправления ошибок в результате автоматического распознавания отсканированного текста или записей речи.

5.                 В приложениях, связанных с автоматической обработкой текстов.

Функция Левенштейна может играть роль фильтра, заведомо отбрасывающего неприемлемые варианты (у которых значение функции больше некоторой заданной константы).

Допустим, имеются слова Текст и Тост. Необходимо преобразовать одно слово в другое, используя только операции: удаления, добавления и замены.

Текст Тост – исходное состояние

Шаг 1. Токст Тост (замена)

Шаг 2. Тост Тост (удаление)

Таким образом, для вычисления расстояния Левенштейна от строки Текст до строки Тост потребовалось два шага. В данном случае, расстояние будет равно двум.

Формальное определение

Пусть S₁ и S₂ - две строки (длиной n и m соответственно) над некоторым алфавитом, тогда редакционное расстояние d(S₁,S₂) можно подсчитать по следующей рекуррентной формуле:

,

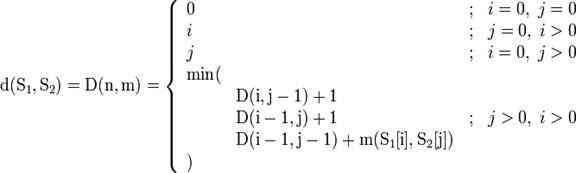где m(a,b) равна нулю, если a = b и единице в противном случае;

min(a,b,c) возвращает наименьший из аргументов.

Рассмотрим формулу более подробно. Здесь шаг по i символизирует удаление (D) из первой строки, по j - вставку (I) в первую строку, а шаг по обоим индексам символизирует замену символа (R) или отсутствие изменений (M). Очевидно, что редакционное расстояние между двумя пустыми строками равно нулю. Так же очевидно то, что чтобы получить пустую строку из строки длиной i, следует совершить i операций удаления, а чтобы получить строку длиной j из пустой, требуется произвести j операций вставки. В нетривиальном случае необходимо выбрать минимальную «стоимость» из трёх вариантов. Вставка/удаление будет в любом случае стоить одну операцию, а вот замена может не понадобиться, если символы равны - тогда шаг по обоим индексам бесплатный. Формализация этих рассуждений приводит к формуле, указанной выше.

Очевидно, справедливы следующие утверждения:

1.    

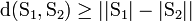
2.    

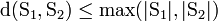
3.    

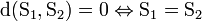
Продолжая пример, построим матрицу преобразования Текст в Тост.

Изначально матрица выглядит, как показано в таблице 1

Таблица 1. Изначальное состояние матрицы.

Проставление значений в матрице происходит по следующей формуле:

а(i,j)= min( а(i-1,j)+1; а(i,j-1)+1; а(i-1,j-1)+ if(S[i]=S[j],0,1) ),

if(S[i]=S[j],0,1) – возвращает 0, если буквы, стоящие в соответствующих позициях одинаковы, 1 если различаются.

Следовательно, чтобы получить значение элемента необходимо узнать значения его соседей сверху, снизу и по диагонали. Для элемента а(1,1) получается:

а(1,1) = min( а(0,1)+1; а(1,0)+1; а(0,0)+ if(S[1]=S[1],0,1) ),

а(1,1) = min( 2; 2; 0+ if(Т=Т, 0, 1) ) = min( 2; 2; 0 ) = 0

а(1,2)= min( а(0,2) +1; а(1,1) +1; а(0,1)+ if(Т=О,0,1) ),

а(1,2)= min( 3; 1; 1+ if(Т=О,0,1) ) = min( 3; 1; 2 )=1

… и тд

В итоге получаем матрицу, значение элемента a(n,m) которой равно расстоянию Левенштейна от S₁ =Тост до S₂=Текст.

Таблица 2. Заполненная матрица.

Трудоемкость алгоритма

Алгоритм в виде, описанном выше, требует O(m*n) операций и такую же память. Если требуется только расстояние, легко уменьшить требуемую память до O(min(m,n)).

Однако всё несколько усложняется, если требуется также найти редакционное предписание. В таком случае снижение использования памяти возможно только за счёт понижения производительности. Наиболее широко распространены следующие варианты (n = max( | S₁ | , | S₂ | )):

·        O(n²) времени и O(n²) памяти;

При вычислении редакционного расстояния хранятся все шаги, затем предписание восстанавливается явно, возвращаясь по сохранённым шагам.

·        O(n³) времени и O(n) памяти;

Хранится только две строки - текущая и предыдущая. Для восстановления предписания O(n) раз идут до текущего элемента (после каждого раза его индекс уменьшается на O(1).

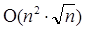·                  времени и  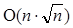памяти.

Метод схож с предыдущим, только каждый раз хранятся полосы высотой 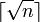, а индекс уменьшается на .

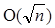Реализация алгоритма на языке PL/SQL

CREATE OR REPLACE FUNCTION LD (

  as_src_i                         IN VARCHAR2

, as_trg_i                         IN VARCHAR2)

RETURN NUMBER

DETERMINISTIC

AS

  ln_src_len    PLS_INTEGER := NVL(LENGTH(as_src_i), 0);

  ln_trg_len    PLS_INTEGER := NVL(LENGTH(as_trg_i), 0);

  ln_hlen       PLS_INTEGER;

  ln_cost       PLS_INTEGER;

  TYPE t_numtbl IS TABLE OF PLS_INTEGER INDEX BY BINARY_INTEGER;

  la_ldmatrix                         t_numtbl;

BEGIN

  IF    (ln_src_len = 0) THEN RETURN ln_trg_len;

  ELSIF (ln_trg_len = 0) THEN RETURN ln_src_len;

  END IF;

  ln_hlen := ln_src_len + 1;

  FOR h IN 0 .. ln_src_len

  LOOP  la_ldmatrix(h) := h;

  END LOOP;

  FOR v IN 0 .. ln_trg_len

  LOOP     la_ldmatrix(v * ln_hlen) := v;

  END LOOP;

  FOR h IN 1 .. ln_src_len

  LOOP

    FOR v IN 1 .. ln_trg_len

    LOOP

      IF (SUBSTR(as_src_i, h, 1) = SUBSTR(as_trg_i, v, 1))

      THEN

        ln_cost := 0;

      ELSE

        ln_cost := 1;

      END IF;

      la_ldmatrix(v * ln_hlen + h) :=

         LEAST(

           la_ldmatrix((v - 1) * ln_hlen + h    ) + 1

         , la_ldmatrix( v      * ln_hlen + h - 1) + 1

         , la_ldmatrix((v - 1) * ln_hlen + h - 1) + ln_cost

         )

      ;

    END LOOP;

  END LOOP;

  RETURN la_ldmatrix(ln_trg_len * ln_hlen + ln_src_len);

END ld;

Заключение.

Полученные в ходе программной реализации и тестирования рассмотренной функции Левенштейна D(n,m) на различных базах данных результаты позволяют сделать выводы об оправданности применения расстояния Левенштейна в тех случаях, когда нужна грубая, но быстродействующая категоризация, а также для устранения опечаток, когда данные содержат лишние или пропущенные символы. Наиболее приемлемые результаты алгоритм показал для устранения опечаток следующих трех наиболее распространенных типов:

1. Пропущенная буква.

2. Лишняя буква/символ.

3. Нарушенный порядок букв в слове («перепутанные» буквы).

Для поиска более точных различий между словами рекомендуется использовать другие алгоритмы, например N-Gram, расширенной выборки, деревья поиска и другие.

Литература:

1.      Левенштейн В.И. Двоичные коды с исправлением выпадений, вставок и замещений символов. Докл. АН СССР, 1965,163, 4, с. 845-848.

2. Web site of the Computer science department of Maryland University. Research on N-Grams in Information Retrieval. http://www.cs.umbc.edu/ngram/
3. А.В. Левитин. Алгоритмы: введение в разработку и анализ.  «Вильямс», 2006. С. 392-398.
4. H. Shang, T.H. Merret. Tries for Approximate String Matching. In IEEE Transactions on Knowledge and Data Engineering, volume 8(4), pages 540 – 547, 1996.
5. E. Ukkonen. Algorithms for approximate string matching. In Information and Control, volume (64), pages 100-118, 1985.
6. E. Ukkonen. Finding approximate patterns in strings, O(k * n) time. In Journal of Algorithms volume 6, pages 132-137, 1985.
7. E. Ukkonen. Approximate String Matching with q- Grams and maximal matches. In Theoretical Computer Science, volume 92(1), pages 191-211, 1992.