Математическая модель опухоли щитовидной железы



Разработана математическая модель роста злокачественной опухоли щитовидной железы, представляющая собой краевую задачу для системы дифференциальных уравнений в частных производных. Учитываются основные биохимические реакции, протекающие в щитовидной железе: клетки опухоли считаются агрессивными по отношению к процессам, происходящим в функциональном пространстве. Исследуется устойчивость стационарных состояний. Решение нелинейных уравнений строится с применением численных методов.

Ключевые слова: математическое моделирование, дифференциальные уравнения, щитовидная железа, ферментативная реакция, новообразование.

Введение. Математическому моделированию злокачественных опухолей, возникающих в организмах млекопитающих, посвящено достаточно много работ [1, 16, 17, 18, 20, 21, 28, 30]. В большинстве из них разрабатываются модели роста новообразований как без учета работы органов, в окрестности которых они возникают, так и модели конкретных видов опухолей. Одной из не простых задач является построение математических моделей работы щитовидной железы и моделей нарушений ее функций [4, 13, 14].

Математическая модель функционирования щитовидной железы, в которой учитываются основные биохимические реакции, протекающие в ней: поступление йода, связывание его с тиреоглобулином с последующим образованием и накоплением гормона разработана в [2, 34]. Модель представлена задачей Коши для системы трех обыкновенных дифференциальных уравнений.

Основные биохимические реакции. Функциональной единицей щитовидной железы является шарообразный фолликул, состоящий из коллоида и окружающих его фолликулярных клеток (тироцитов) [12–14, 25, 31, 32]. В фолликулярные клетки поступает йод (I), который после активизации ферментами поступает в коллоид. В коллоиде в результате связывания йода с молекулами тиреоглобулина (Tg) образуются тиреоидные гормоны, 95 % из которых составляет гормон тироксин (Т4). Гормоны хранятся в коллоиде, а при снижении их уровня в сыворотке крови гормоны отделяются от тиреоглобулина и в свободном виде попадают в кровоток, где и выполняют свои регуляторные функции [5, 14].

Недостаток йода в организме вызывает и недостаток гормона T4, а избыток йода — избыток гормона. В обоих случаях реакцией организма на изменение количества вырабатываемого гормона может являться команда на увеличении объема щитовидной железы в первом случае направленное на увеличение выхода гормона T4, а во втором на — необходимость переработать избыточный йод.

Из клеток фолликулярного эпителия могут происходить различные типы новообразований, отличающиеся строением и молекулярно-биологическими характеристиками [4, 11, 22, 24, 27]. Ткань опухоли состоит из рядов мелких, плотно прилегающих друг к другу клеток, расположенных среди материнской ткани железы. Рост опухоли щитовидной железы сопровождается увеличением количества «нефункциональных» клеток, с малым количеством фолликулов или вовсе без их образования, вытеснением работающих фолликулов опухолевыми клетками, уменьшением общего рабочего объема фолликул щитовидной железы и, в конечном итоге, может произойти полное замещение «функционального» пространства клетками опухоли, не несущих функциональную нагрузку по синтезу тиреоидных гормонов [4, 14].

Математическая модель функционирования щитовидной железы. В модели коллоид и окружающие его многочисленные фолликулы считаются единым целым, равномерно распределенными по всему функциональному пространству, занимаемому щитовидной железой. Учитываются основные процессы, происходящие в железе: поступление внешнего активного йода, присоединение йода к тиреоглобулину, образование гормона Т4, его связывание с тиреоглобулином и высвобождение гормона Т4 через внешнюю оболочку железы [14]. Тиреоглобулин сохраняется в железе, во внешнюю среду не поступает. Предполагается, что среда, в которой происходят реакции, является гомогенной [6, 7, 19].

С учетом этих гипотез, система дифференциальных уравнений, описывающая процессы, происходящие в щитовидной железе, имеет следующий вид [34]:

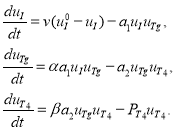(1)

В этих уравнениях — концентрация активного йода в железе, — концентрация тиреоглобулина, — концентрация гормона Т4; — проницаемость внешней мембраны железы, — скорость поступления йода в железу, — равновесная концентрация йода, , , , — положительные константы, характеризующие скорости реакций.

Первое уравнение в (1) описывает скорость изменения концентрации йода: поступление йода в коллоид и выход его остатков (слагаемое ) и скорость связывания йода с тиреоглобулином (слагаемое ). Второе уравнение в (1) описывает скорость изменения концентрации тиреоглобулина: слагаемое — скорость образования тиреоглобулина, слагаемое — скорость связывания тиреоглобулина с гормоном Т4. Третье уравнение в (1) описывает процесс образования тиреоидного гормона Т4: слагаемое — скорость образования гормона Т4, слагаемое — скорость выхода гормона Т4 через внешнюю мембрану железы в кровеносное русло.

С учетом опубликованных в литературных источниках данных по скоростям реакций [7, 8], конверсии йода (90 %) и отношению концентрации гормона к концентрации тиреоглобулина (4:1) [3, 9, 10, 23, 27], в модели за единичную принята константа . Тогда , , , , , , . При принятом наборе констант единица измерения времени в модели соответствует 30 суткам, а концентрации веществ считаются безразмерными. При этом в стационарном состоянии , , . Эта стационарная точка рассматривается как «естественное» положение равновесия, а отклонение от него считается нарушением функции щитовидной железы.

Система уравнений (1) имеет две стационарных точки

,

и

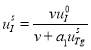, , .(2)

Как показано в [34] первая стационарная точка неустойчивая. Неустойчивость этого положения равновесия рассматривается как начало естественного функционирования щитовидной железы. Вторая стационарная точка устойчивая [34]. При принятых значениях констант матрица Якоби правой части уравнений (1) в этой стационарной точке имеет одно отрицательное собственное значение и пару комплексно сопряженных с отрицательной вещественной частью [34]. То есть при небольших изменениях констант система через затухающие колебания перейдет в новое положение равновесия.

Модель опухоли щитовидной железы. Одной из возможных причин нарушения работы щитовидной железы может являться возникновение опухоли. В модели предполагается, что рост возникшей опухоли сопровождается уничтожением работающих фолликул, уменьшением рабочего объема щитовидной железы и, в конечном итоге, полным замещением «функционального» пространства клетками опухоли. При этом считается, что постоянно растущие клетки опухоли не выполняют функциональную нагрузку по синтезу гормонов [11, 14, 21, 29, 30].

Экспериментальные данные по кинетике роста различных тканей говорят о их экспоненциальном росте [11, 22, 26]. Если — концентрация опухолевых клеток, то кинетика ее собственного неограниченного роста описывается уравнением [8, 11]

,

где — константа. По данным исследования [12], константа для роста опухоли у мышей изменялась в зависимости от опыта в диапазоне 0.01 до 0.1 1/день [14]. По данным клинических исследований для человека она составляла около 0.001 1/день [12].

В модели опухоли предполагается, что возникшие опухолевые клетки размножаются, поглощая и и замещая, таким образом, их. Скорость убыли и за счет опухолевых клеток пропорциональна их количеству и количеству опухолевых клеток. При этом предполагается, что при полном вытеснении и из функционального пространства опухоль перестает расти. Скорость роста опухолевых клеток считается пропорциональной сумме в текущий момент времени. Поскольку в стационарном состоянии и , то в модели принимается, что должно выполняться неравенство . Увеличение количества опухолевых клеток сопровождается и уменьшением поступления йода, а при йод перестает поступать. Щитовидная железа представлена сферой радиуса .

Тогда математическая модель щитовидной железы с растущей в ней опухолью представляется системой дифференциальных уравнений

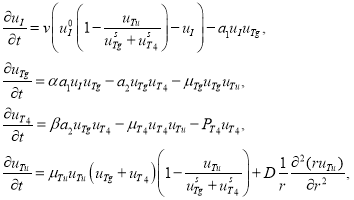(3)

где , и — константы, — коэффициент диффузии опухолевых клеток.

В первом уравнении скорость поступления йода в щитовидную железу описывается функцией и становится равной нулю, если опухоль займет все функциональное пространство. Во втором уравнении слагаемое — скорость поглощения опухолевыми клетками тиреоглобулина считается пропорциональной их концентрациям, а слагаемое в четвертом уравнении — скорость поглощения опухолевыми клетками гормона . Опухоль в рамках предлагаемой модели растет за счет поглощения тиреоглобулина и гормона . Скорость ее роста принята в соответствии с экспериментальными данными [8, 23] пропорциональной произведению . Поскольку первоначальная суммарная концентрация тиреоглобулина и гормона равна , то при достижении этого значения рост опухоли должен прекратиться. Это обеспечивается множителем в четвертом уравнении.

К системе уравнений (3) необходимо добавить граничные и начальные условия. Если опухоль возникает в начальный момент времени, и при этом система уравнений (3) находится в стационарном положении равновесия, то в качестве начальных условий (при ) берутся

, , ,

,

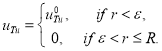где , а малая положительная величина. То есть, предполагается, что опухолевые клетки возникают в центре сферы в малом количестве.

В качестве граничных условий берутся условие ограниченность функции в центре сферы и равенство нулю потока опухолевых клеток через поверхность сферы:

и при .(4)

Гомогенные решения. Стационарная система уравнений (3) имеет два гомогенных решения.

Первое решение

, , ,

соответствует случаю отсутствия опухолевых клеток. В окрестности этого решения для малых значений четвертое уравнение в (3) принимает вид

.

Решение этого уравнения представляется в виде тригонометрического ряда

.

Это решение будет удовлетворять условиям (4), если значения () являются корнями уравнения . Постоянные коэффициенты находятся из удовлетворения начальным условиям.

При выполнении неравенства функция будет убывающей функцией времени независимо от ее значения в начальный момент времени и, соответственно, рассматриваемое гомогенное решение будет неустойчивым [15].

Второе решение

, , ,

соответствует прекращению функционирования щитовидной железы. Пусть наряду с эти решением существует близкое к нему решение

, , ,

такое, что , , — малые положительные величины, а малая по сравнению с величина. Тогда линейное приближение системы уравнений (3) в окрестности рассматриваемой стационарной точки имеет вид

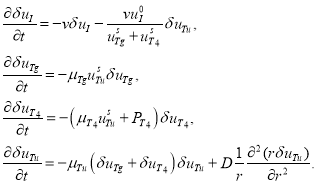(5)

Как следует из второго и третьего уравнений в (5) и будут положительными убывающими функциями времени. Поэтому и при граничных условиях (4) будет также убывающей функцией времени. Поэтому второе гомогенное решение будет устойчивым.

Система уравнений (3) является нелинейной. Построить ее аналитическое решение не представляется возможным. Построение численного решения уравнений (3) осуществлялось на основе дискретизации дифференциальных операторов — производные по пространственной переменной аппроксимировались разностными отношениями. Полученная система нелинейных обыкновенных дифференциальных уравнений решалась предложенными в [33] методами.

На рисунке для случая констант , , , , , , , , , представлено решение в моменты времени . Как показал анализ численных экспериментов, в первом приближении решение представляет собой волну, распространяющуюся со скорость .

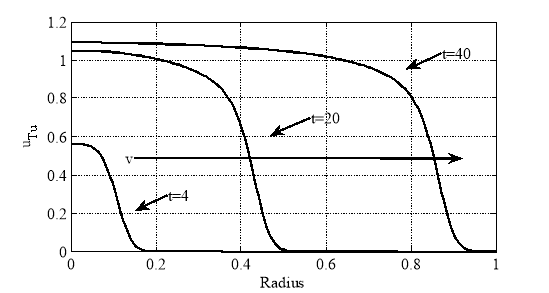
Как следует из полученных результатов, рост опухоли можно интерпретировать как движение автоволны.

Литература:

1. Anderson A. R. A. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion // Mathematical Medicine and Biology. — 2005. — no. 22. — 163–186.
2. Balykina Ju.E., Kolpak E. P., Kotina E. D. Mathematical Model of Thyroid Function // Middle-East Journal of Scientific Research. — 2014. — V. 19. — no. 3. — PP. 429–433.
3. Berson S. A., Yalow R. S. Quantitative Aspects of Iodine Metabolism. The Exchangeable Organic Iodine Pool, and the Rates of Thyroidal Secretion, Peripheral Degradation and Fecal Excretion of Endogenously Synthesized Organically Bound Iodine // J. Clin. Invest. — 1954. — V. 33. — no. 11. — PP. 1533–1552.
4. Carpi A., Mechanick J. I. Thyroid Cancer from Emergent Biotechnologies to Clinical Practice Guidelines. CRC Press Taylor & Francis Group. London, New York. 2011. 382 p.
5. Danziger L., Elmergreen G. L. The thyroid-pituitary homeostatic mechanism // The bulletin of mathematical biophysics. — 1956. — V. 18. — no. 1. — PP. 1–13.
6. Degon M, Chipkin S. R., Hollot C. V., Zoeller R. T., Chait Y. A computational model of the human thyroid // Math. Biosci. — 2008. — V. 212. — no. 1. — PP. 22–53.
7. Distefano J. J., Mak P. H. Optimal control policies for the prescription of thyroid hormones // Math. Biosci. — 1978. — V. 42. — no. 3–4. — PP. 159–186.
8. Edna F. PK-PD modeling of combination efficacy effect from administration of the MEK inhibitor GDC-0973 and PI3K inhibitor GDC-0941 in A2058 xenografts // Cancer Chemotherapy Pharmacol. — 2013. — V. 71, no. 1. — PP. 133–143.
9. Eisenberg M., Samuels M., DiStefano J. J. III. Extensions, validation, and clinical applications of a feedback control system simulator of the hypothalamo-pituitary-thyroid axis // Thyroid. — 2008. — V. 18. — no. 10. — PP. 1071–1085.
10. Hoermann R., Midgley J. E. M., Larisch R., Dietrich J. W. Is Pituitary Thyrotropin an Adequate Measure Of Thyroid Hormone-Controlled Homeostasis During Thyroxine Treatment? // European Journal of Endocrinology. — 2012. — V. 168. — no. 2. — PP. 271–280.
11. Jackiewicza Z., Jorcykb C. L., Kolevc M., Zubik-Kowald B. Correlation between animal and mathematical models for prostate cancer progression // Computational and Mathematical Methods in Medicine. — 2009. — Vol. 10. — No. 4. — pp. 241–252.
12. Jian-Feng Lu. Population pharmacokinetic/pharmacodynamic modeling for the time course of tumor shrinkage by motesanib in thyroid cancer patients // Cancer Chemotherapy Pharmacol. — 2010. — V. 66. — no. 6. — P. 1151–1158.
13. Jugan M.-L., Levi Y., Blondeau J.-P. Endocrine Disruptors and Thyroid Hormone Physiology // Biochemical Pharmacology. — 2010. — v. 79. — 939–947.
14. Kettyle W. M., Arky R. A. Endocrine path physiology. New York. Lippincott — Raven. — 1998. 336 p.
15. King A. C., Billingham J., Otto S. R., Differential equation. Linear. Nonlinear. Ordinary. Partial. Cambridg. University press. — 2003. — 541 p.
16. Kolev M., Zubik-Kowal B. Numerical Solutions for a Model of Tissue Invasion and Migration of Tumour Cells // Computational and Mathematical Methods in Medicine Volume 2011, Article ID 452320, 16 pages doi:10.1155/2011/452320.
17. Kolobov A. V., Kuznetsov M. B. The study of angiogenesis effect on the growth rate of an invasive tumor using a mathematical model // Russ. J. Numer. Anal. Math. Modelling. — Vol. 28. — No. 5. — pp. 471–483 (2013).
18. Lamooki G. R. R., Shirazi A. H., Mani A. R. Dynamical model for thyroid // Commun Nonlinear Sci Numer Simulat. — 2015. — V. 22. — pp. 297–313.
19. Leow M. K. S. A mathematical model of pituitary-thyroid interaction to provide an insight into the nature of the thyrotropin-thyroid hormone relationship // Journal of Theoretical Biology. — 2007. — V. 248. — no. 2. — PP. 275–287.
20. Macklin P., McDougall S., Anderson A. R. A., Chaplain M. A. J. Lowengrub V. C. J. Multiscale modelling and nonlinear simulation of vascular tumour growth // J. Math. Biol. — 2009. — v. 58:765–798.
21. Marciniak-Czochra A., Kimmel M. Dynamics of growth and signaling along linear and surface structures in very early tumors // Computational and Mathematical Methods in Medicine. — 2006. — V.7. — no. 2–3. — pp. 189–213.
22. Martin T. A., Parr C., Davies G., Watkins G., Lane J., Matsumoto K., Nakamura T., Robert E.Mansel R. E., Jiang W. G. Growth and angiogenesis of human breast cancer in a nude mouse tumour model is reduced by NK4, a HGF/SF antagonist // Carcinogenesis. — 2003. — V. 24. — no.8. — pp.1317–1323.
23. McInerney D., Schnell S., Baker R. E., Maini P. K. A mathematical formulation for the cell cycle model in somitogenesis: analysis, parameter constraints and numerical solutions // Mathematical Medicine and Biology — 2004. — V. 21. — no. 2. — PP. 85–113.
24. Parameswaran R. Molecular pathogenesis of follicular cell derived thyroid cancers / Parameswaran R., Brooks S., Sadler G. P. // Int. Journal of Surgery. — 2010. — no. 8. — РP. 186–193.
25. Riggs D. S. Quantitative aspects of iodine metabolism in man // Pharmacology Rev. — 1952. — V. 4. — no. 3. –PP. 284.
26. Rupik W. Structural and ultrastructural differentiation of the thyroid gland during embryogenesis in the grass snake Natrix natrix L. (Lepidosauria, Serpentes) // Zoology. — 2011. — v. 114. — pp. 284– 297.
27. Segev D. L., Umbricht C., Zeiger M. A. Molecular pathogenesis of thyroid cancer // Surg Oncol. — 2003. — V. 12. — no. 2. pp. 69–90.
28. Simpson M. J., Foy H. B., McCue S. W. Travelling waves for a velocity-jump model of cell migration and proliferation // Mathematical Biosciences. — 2013. — v. 244. — pp. 98–106
29. Takano T. Fetal cell carcinogenesis of the thyroid: Theory and practice // Seminars in Cancer Biology. — 2007. — V. 17. — no. 3. — P. 233–240.
30. Tindall M. J., Please C. P., Peddie M. J. Modelling the formation of necrotic regions in avascular tumours // Mathematical Biosciences. — 2008. — v. 211. — 34–55
31. Toda S., Aoki S., Suzuki K. et al. Thyrocytes, but not C cells, actively undergo growth and folliculogenesis at the periphery of thyroid tissue fragments in three-dimensional collagen gel culture // Cell and Tissue Research. — 2003. — V. 312. — no. 3. — PP. 281–289.
32. Toda S., Koike N., Sugihara H. Thyrocyte integration, and thyroid folliculogenesis and tissue regeneration: perspective for thyroid tissue engineering // Pathology International. — 2001. — V. 51. — no. — 6. — PP. 403–417.
33. Балыкина Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вест. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. — 2013. — Вып. 3. — С. 20–31.
34. Колпак Е. П., Терехина Е. И. Математическая модель функционирования щитовидной железы // Молодой ученый. — 2018. — № 4(190). — С. 1–6.