In mathematics, the Cesàro means of a sequence ![]() are the terms of the sequence
are the terms of the sequence ![]() , where
, where
![]() is the arithmetic mean of the first n elements of
is the arithmetic mean of the first n elements of ![]() .
.
This concept is named after Ernesto Cesàro (1859–1905).
A basic result states that the limit of a convergent sequence equals the limit of its Cesàro mean. That is, the operation of talking Cesàro means preserves the convergence and the limit of a sequence. This is the basis for using Cesàro means in summability method in the theory of divirgent series.
Let m space of really limited sequences with norm ![]() where
where ![]() . It is known that, m is a complete bordered space. We denote by
. It is known that, m is a complete bordered space. We denote by ![]() the space of convergent sequence. It is obvious that,
the space of convergent sequence. It is obvious that, ![]() is a closed sub-space in
is a closed sub-space in ![]() . Next, we denote by
. Next, we denote by ![]() the subset of
the subset of ![]() consisting of sequence of convergent in Cesàro mean, i.e
consisting of sequence of convergent in Cesàro mean, i.e
![]() if, exist limit
if, exist limit ![]() , where
, where ![]()
Let the operator ch Cesàro be the operator associated with the ![]() sequence
sequence ![]() . We denote by
. We denote by ![]() set of sequence of
set of sequence of ![]() , for which
, for which ![]() it is easy to notice that,
it is easy to notice that, ![]()
Let ![]()
Statement 1
All ![]() are a linear subspace of
are a linear subspace of ![]()
Task 1
Whether ![]() closed subspace when
closed subspace when ![]() ?
?
We consider sequences of m, such that ![]() or 1
or 1
Task 2
Does ![]() conformity m?
conformity m?
Definition 1. Let us given the sequence ![]() . If the sequence
. If the sequence ![]() which consist of elements of the sequence
which consist of elements of the sequence ![]() converges to
converges to ![]() then the sequence
then the sequence ![]() converges to
converges to ![]() in Cesàro mean.
in Cesàro mean.
Example. Let us consider the following sequence
![]()
We have an oscillating sequence, but in the Cesàro means it has limit ![]()
![]()
![]()
So, the sequence ![]() converges to
converges to ![]() in Cesàro mean.
in Cesàro mean.
Suppose given the sequence
![]()
Where ![]() are terms of arithmetic progression.
are terms of arithmetic progression.
Theorem 1. If ![]() are the terms of arithmetic progression, where
are the terms of arithmetic progression, where ![]() and
and ![]() then sequence (1) is convergent in Cesàro mean.
then sequence (1) is convergent in Cesàro mean.
Proof. ![]()
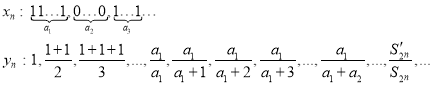
Where ![]() sum of odd members of arithmetic progression,
sum of odd members of arithmetic progression,
![]() sum of all members of arithmetic progression.
sum of all members of arithmetic progression.
Then sequence (1) is convergent in Cesàro mean to ![]()
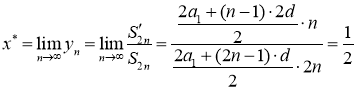
![]() .
.
Theorem 2. If ![]() are terms of geometric progression, where
are terms of geometric progression, where ![]() and
and ![]() when
when
then sequence ![]() is not convergent in Cesàro mean.
is not convergent in Cesàro mean.
Proof.
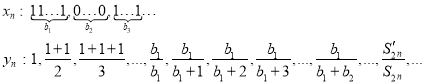
Where ![]() sum of odd members of geometric progression,
sum of odd members of geometric progression,
![]() sum of all members of geometric progression.
sum of all members of geometric progression.
then sequence ![]() is not convergent in Cesàro mean
is not convergent in Cesàro mean
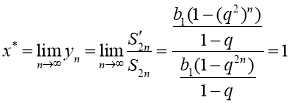 .
.
Definition 2. Let us given the sequence ![]() . The sequences
. The sequences ![]() and
and ![]() whose consist of elements of the sequences
whose consist of elements of the sequences ![]() and
and ![]() accordingly. If the second sequence
accordingly. If the second sequence ![]() converges to
converges to ![]() then the sequence
then the sequence ![]() has the second convergence to
has the second convergence to ![]() in Cesàro mean.
in Cesàro mean.
Theorem 3. If ![]() are the terms of geometric progression, where
are the terms of geometric progression, where ![]() and
and ![]()
Then the sequence (2) has the second convergence in Cesàro mean.
Proof.
Suppose given the sequence ![]() such that
such that
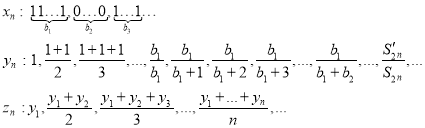
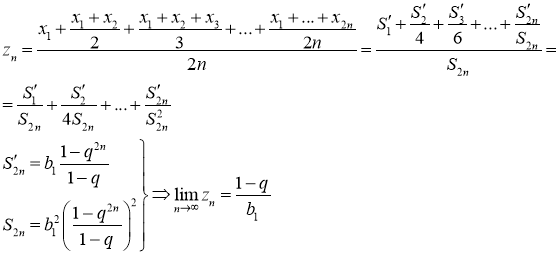
Where ![]() sum of odd members of geometric progression,
sum of odd members of geometric progression,
![]() sum of all members of geometric progression.
sum of all members of geometric progression.
Then sequence (2) is convergent in Cesàro mean to ![]()
References:
- Hardy, G.H.(1992). Divergent Series. Providence: American Mathematical Society. ISBN 978–0-8218–2649–2
- Katznelson, Yitzhak (1976). An Introduction to Harmonic Analysis. New York: Dover publications. ISBN 978–0-486–63331–2







