В хорошо известной модели светового излучения (так называемой модели “спин-бозон”, см. [1–3]) предполагается, что атом, который может находиться в двух состояниях — основном с энергией — 
и возбужденном с энергией , испускает и поглощает фотоны, переходя из одного состояния в другое. Оператор энергии такой системы обозначим через 
.
Задача о полном спектральном описании оператора представляется довольно трудной. В связи с этим будет естественно рассмотреть упрощенные (“урезанные”) модели, отличающиеся от модели тем, что возможное число фотонов в них ограничено и не превосходит 
. В настоящей работе рассматриваем случай 
. Гильбертовым пространством состояний такой модели служит пространство ℋ:=
, где 
— двумерное комплексное пространство и 
гильбертово пространство квадратично — интегрируемых функций, определенных на 
-мерном торе 
со значениями в 
.
Рассмотрим оператор 
задающийся как 
блочно-операторная матрица
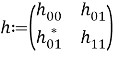
c матричными элементами 
, 
,
Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирований, 
, 
сопряженный оператор к 
, 
энергия фотона с импульсом 
, 
вещественная непрерывная функция на и 
— “параметр взаимодействия”. При этом 
есть непрерывная функция на и
.
В таких предположениях оператор
является ограниченным и самосопряженным оператором в ℋ.
Можно показать, что
В непрерывном случае 
существенный спектр соответствующей модели состоит из полуоси 
, а в данном случае видно, что существенный спектр оператора есть объединение двух отрезков конечной длины, причем они не пересекаются при 
.
Определим регулярную в 
функцию
.
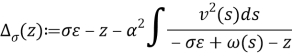Установим связь между собственными значениями оператора и нулями функции 
.
Лемма 1. Число 
является собственным значением оператора тогда и только тогда, когда 
.
Из леммы 1 вытекает, что
Теперь опишем резольвенты оператора . Сначала отметим, что для спектра оператора имеет место равенство
.
При каждом фиксированном 
введем блочно-операторную матрицу 
размером 2
2, действующую в ℋ как
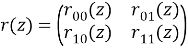, (1)
где матричные элементы 
определяются равенствами:
,
.
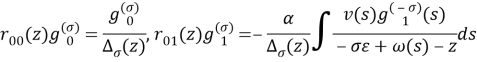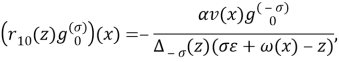
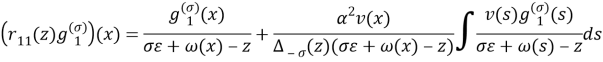Здесь 
.
Основным результатом настоящей работы является следующая теорема.
Теорема 1. При каждом фиксированном резольвента 
оператора действует по формуле (1).
При доказательстве теоремы 1 используются элементы функционального анализа. Обычно с помощью детального исследования резольвенты доказывается существования соответствующего обратного волнового оператора.
Автор приносит благодарность к. ф.-м.н., доц. Т. Х. Расулову за постановку задачи и обсуждение результатов работы.
Литература:
- M. Huebner, H. Spohn. Spectral properties of spin-boson Hamiltonian. Annales de l`Institut Henri Poincare, 62:3 (1995), 289–323.
- R. A. Minlos, H. Spohn. The three-body problem in radioactive decay: the case of one atom and at most two photons. Topics in Statistical and Theoretical Physics, American Mathematical Society Translations-Series 2, 177 (1996), 159–193.
- H. Spohn. Ground states of the spin-boson Hamiltonian. Communications in Mathematical Physics, 123 (1989), 277–304.
