В данной работе рассматриваются неравномерные оценки для последовательности симметрично зависимых случайных величин. В работе [1] изучены теоретико-вероятностные проблемы для вероятностных мер со значениями в пространствах измеримых функций. Будем придерживается определения и обозначения этой работы.
Пусть (T,
) — измеримое пространство, т. е. множество T с выделенной Ϭ — алгеброй его подмножеств. Через S=S(T,) будем обозначать совокупность всех измеримых относительно Ϭ- алгебры 
на пространстве T.
Множество S образует алгебру относительно операций точечного умножения, сложения функций и поточечного умножения на скаляр.
Пусть (T,
) — вероятностное пространство, т. е. измеримое пространство (T,) с числовой вероятностной мерой 
, определенной на элементах Ϭ –алгебры Σ.
Обозначим через 
идеал алгебры S(T,) состоящий из тех функций из S(T,), которые m –п. в. равны нулю.
Фактор алгебру L0(T,
) = S(T,
)/ 
обозначим через E.
Через 
обозначим класс содержащей x. Нуль и единица алгебры E обозначаются соответственно через 
и 1.
Пусть Ω -непустое множество и F- некоторая алгебра его подмножеств.
Определение 1. E-значной вероятностью на измеримом пространстве (Ω, F) называется Ϭ-аддитивная функция P: F 
{x
, 
≤x≤1 }такая, что P(Ω)=1.
Определение 2. Говорят что пространство (Ω, F,P)сE-значной вероятностью P обладает полноты, если M
A
F, P(A)= , то M 
F и P(M)= .
Пусть Γ –конечныйили бесконечный класс подмножестве из F.
Определение 3. Множества из Γ называются P — независимыми, если
P(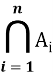
) =
)
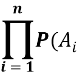для любого конечного набора { Ai, i=1,2, …,n} различных множеств из Γ.
Пусть 
— Ϭ — подалгебры Ϭ — алгебры F.
Определение 4. Вероятность P назовем однородной (или E — однородной) если
P(A
B)=
P(B)
для любого A
, B
F (I(A)- индикатор события A).
E-значные вероятности со свойством E-однородности возникают при рассмотрении условных вероятностей.
Действительно, пусть (Ω,F,P) –вероятностные пространство с числовой вероятностью Р, G — Ϭ-алгебра в F и 
: A F (A) ∈ S(Ω, G) — один из вариантов условной вероятности относительно Ϭ-подалгебры G.
Если E= L0(Ω,G,P) –совокупность классов P-эквивалентных случайных величин из S(Ω, G), то условная вероятность 
определяет на (Ω, F) E-значную вероятность
P(A) =
, A
F.
В этом случае, E-значное математическое ожидание M
=
случайной Ω величина 
есть просто условное математическое ожидание 
, а E-значная функция распределения 
P{
< 
} есть условная функция распределения
(
) = 
, 
.
При этом P- независимость в точности совпадает с понятием условной независимости относительно Ϭ — подалгебры G.
В работа [2] автором получены неравномерные оценки для последовательности P-независимых случайных величин. В случае, когда вероятность P однородный (или E — однородный) как следствие этого результата можно получить следующую неравномерную оценку для последовательности условно независимых случайных величин.
Теорема 1. Пусть (Ω, F,P) — вероятностное пространство с числовой вероятностью P, G- Ϭ — подалгебра F и 1, 2,
n,…- последовательность условно независимых случайных величин относительно Ϭ — подалгебры G.
Пусть существуют P-п.в. конечные третьи условные моменты
и 
=
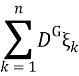>0 P — п.в..
Тогда |
(
) — Φ() |
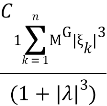P- п.в.,
где () = 
{
(
1+ 2
n)<λ }, Φ()-стандартная нормальная распределения, 
-абсолютная константа.
Пусть 1, 2,n,…последовательность случайных величин заданных в некатором вероятностном пространстве (Ω, F,P) c числовой вероятностью P.
Определение 4. Последовательности случайных величин
1, 2,n,… назовем симметрично зависимыми, если k-мерная числовая функция распределения 
для любого (
инвариантна относительно перестановок индексов 
,
,…,
(индексы ,,…, предполагаются попарно различными).
Для каждого n
обозначим через Un Ϭ — подалгебру в F, порожденную случайными величинами n, n+1,
и пусть 
=
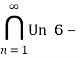алгебра в F асимптотических событий последовательности 1, 2,n,….
Вместо Ϭ — алгебры рассмотрим ее P- пополнение 
, т. е. наименьшую Ϭ — подалгебру в F, содержащую и все множество нулевой вероятности P (сама 
алгебра F предполагается P- полной).
Для симметрично зависимых случайных величин 1, 2,n,… Ϭ –подалгебра совпадает с Ϭ — алгеброй 
= 
, и 
-Ϭ — алгебра, порожденная событиями, симметрично зависящими от 1, 2,n и произвольно зависящими от n+1, n+2,
Теорема 2. (см. например [1]). Если последовательность случайных величин 1, 2,n,… на вероятностном пространстве (Ω,F,P) является симметрично зависимой, то случайные величины 1, 2,n,… являются условно независимыми и имеет одинаковые условные распределения относительно Ϭ — алгебры асимптотических событий последовательности 1, 2,n,….
Обратно, пусть B- произвольная P- полная Ϭ — подалгебра в F и 1, 2,n,… — последовательность случайных величин на (Ω, F,P), которые условно B; тогда случайные величины 1, 2,n,… симметрично зависимы и 
= B. В частности, симметрично зависимые случайные величины 1, 2,n,… независимы в том и только в том случае, когда Ϭ — алгебры вырождена.
С помощью этой теоремы, связывающего понятие, симметричной зависимости случайных величин и условной независимости случайных величин с одной и той же условной функцией распределения из теоремы 1 можно получить следующие неравномерные оценки для последовательности симметрично зависимых случайных величин.
Теорема 3. Пусть 1, 2,n,…- последовательность симметрично зависимых случайных величин на вероятностном пространстве (Ω, F,P) и U= -P-пополнение Ϭ — алгебры асимптотических событий этой последовательности.
Предположим, что существуют P-п. в. конечные третьи условные моменты
и 
=
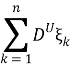>0 P — п. в..
Тогда |
(
) — Φ() |
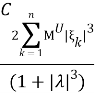P- п. в.,
где, () = 
{
(
1+ 2
n)<λ }, Φ()-стандартная нормальная распределения, 
-абсолютная константа.
Литература:
- Кучкаров Я. Вероятностные распределения со значениями в пространствах измеримых функций. Ташкент, Фан. 1984, 176 стр.
- Мамуров Б. Ж. Неравномерные оценки скорости сходимости в центральной предельной теореме для L0 –значных вероятностей. — Докл. АН УзССР, 1985, № 2, с. 3–5.
