Один из классических методов изучения спектра линейного оператора ![]() в гильбертовом пространстве
в гильбертовом пространстве ![]() — это изучение числового образа этого оператора [1]:
— это изучение числового образа этого оператора [1]:
![]() ,
,
здесь ![]() есть область определения оператора
есть область определения оператора ![]() . Если
. Если ![]() — ограниченный оператор, то
— ограниченный оператор, то ![]() . Известно, что точечный спектр
. Известно, что точечный спектр ![]() оператора
оператора ![]() лежит в
лежит в ![]() , а аппроксимативно точечный спектр
, а аппроксимативно точечный спектр ![]() оператора
оператора ![]() содержится в
содержится в ![]() . Если
. Если ![]() замкнутый оператор и всякая компонента множества
замкнутый оператор и всякая компонента множества ![]() содержит хотя бы одну точку резольвентного множество
содержит хотя бы одну точку резольвентного множество ![]() оператора
оператора ![]() , то имеет место включение
, то имеет место включение ![]() (
(![]() -множество комплексных чисел). В силу теоремы Тёплица — Хаусдорфа числовой образ является выпуклым подмножеством множества
-множество комплексных чисел). В силу теоремы Тёплица — Хаусдорфа числовой образ является выпуклым подмножеством множества ![]() . С одной стороны, свойства выпуклости является важным свойством, например, при доказательстве принадлежности спектра в полуплоскость. Но, числовой образ иногда дает недостаточно хорошую структуру, если спектр состоит из объединения двух не пересекающихся множеств.
. С одной стороны, свойства выпуклости является важным свойством, например, при доказательстве принадлежности спектра в полуплоскость. Но, числовой образ иногда дает недостаточно хорошую структуру, если спектр состоит из объединения двух не пересекающихся множеств.
Учитывая этих неудобств, в работе [2] введено понятие квадратичного числового образа и затем изучены в работах [3,4]. Оно определено, если дано разложение ![]() гильбертово пространство
гильбертово пространство ![]() и
и ![]() , здесь
, здесь ![]() и
и ![]() гильбертово пространства. Тогда оператор
гильбертово пространства. Тогда оператор ![]() всегда записывается как квадратичная блочно-операторная матрица размера
всегда записывается как квадратичная блочно-операторная матрица размера ![]()
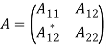 (1)
(1)
с линейными операторами ![]() ,
, ![]() . Для неограниченного линейного оператора
. Для неограниченного линейного оператора ![]() в
в ![]() , его область определении
, его область определении ![]() необязательно должна быть разложимой как
необязательно должна быть разложимой как ![]() c
c ![]() ,
, ![]() и следовательно, это дополнительное предложение, того что оператор
и следовательно, это дополнительное предложение, того что оператор ![]() имел представление (1) такое, что
имел представление (1) такое, что
![]() .
.
Пусть ![]() ,
, ![]() — скалярное произведение и норма в
— скалярное произведение и норма в ![]() ,
, ![]() , соответственно.
, соответственно.
Множество всех собственных значений матрицы
![]()
таких, что
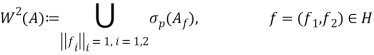
Для двух различных разложений гильбертово пространства ![]() , могут соответствовать различные квадратично числовые образы.
, могут соответствовать различные квадратично числовые образы.
Обозначим через ![]() — множество всех целых, вещественных и комплексных чисел, соответственно.
— множество всех целых, вещественных и комплексных чисел, соответственно.
Пусть ![]() —
— ![]() — мерный тор, т. е. куб
— мерный тор, т. е. куб ![]() — с соответствующим отождествлением противоположных граней. Всюду в работе
— с соответствующим отождествлением противоположных граней. Всюду в работе ![]() рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в ![]() по модулю
по модулю ![]() .
.
Пусть ![]() — гильбертово пространство квадратично — интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично — интегрируемых (комплекснозначных) функций, определенных на ![]() Обозначим через
Обозначим через ![]() прямую сумму пространств
прямую сумму пространств ![]() и
и ![]() , т. е.
, т. е. ![]() .
.
Гильбертово пространство ![]() обычно называется двухчастичным обрезанным подпространством фоковского пространства.
обычно называется двухчастичным обрезанным подпространством фоковского пространства.
В данной статье рассмотрим обобщенную модель Фридрихса ![]() , действующую в гильбертовом пространстве
, действующую в гильбертовом пространстве ![]() как
как ![]() блочно-операторная матрица (1), где элементы
блочно-операторная матрица (1), где элементы ![]()
![]() , определяются по формулам
, определяются по формулам
![]() ,
, ![]() ,
, ![]() ,
, ![]() (2)
(2)
здесь ![]() ;
; ![]() фиксированные вещественные числа,
фиксированные вещественные числа, ![]() вещественнозначная непрерывная функция на
вещественнозначная непрерывная функция на ![]() , а
, а ![]() сопряженный оператор к
сопряженный оператор к ![]() . При этом оператор
. При этом оператор ![]() называется оператором уничтожения, а
называется оператором уничтожения, а ![]() называется оператором рождения.
называется оператором рождения.
Можно проверить, что при таких предположениях операторная матрица ![]() , определенный по формуле (1) с матричными элементами (2), является ограниченным и самосопряженным в гильбертовом пространстве
, определенный по формуле (1) с матричными элементами (2), является ограниченным и самосопряженным в гильбертовом пространстве ![]() .
.
Следующая теорема описывает спектр оператора
Теорема 1. Для спектра оператора ![]() имеет место равенство
имеет место равенство ![]() , т. е. оно имеет чисто точечный спектр, где,
, т. е. оно имеет чисто точечный спектр, где, ![]() — бесконечнократное собственное значение, а
— бесконечнократное собственное значение, а ![]() и
и ![]() — простые собственные значения.
— простые собственные значения.
Следующие две теоремы дают информации о квадратичном числовом образе оператора ![]() .
.
Теорема 2. При ![]() , имеет место равенство
, имеет место равенство ![]() .
.
Для формулировки второго основного результата работы введем следующие множества:
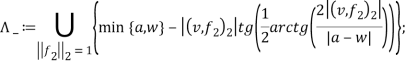
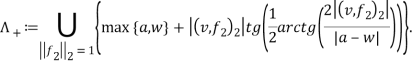
Теорема 3. Если ![]() , то имеет место равенство
, то имеет место равенство ![]() , причём
, причём ![]() .
.
Отметим, что в работе [5] при всех размерностях тора ![]() подробно исследованы числовой образ
подробно исследованы числовой образ ![]() обобщенной модели Фридрихса в терминах матричных элементов. Выделены случаи, когда множество
обобщенной модели Фридрихса в терминах матричных элементов. Выделены случаи, когда множество ![]() замкнуто. Найдены необходимые и достаточные условия для того, чтобы спектр оператора
замкнуто. Найдены необходимые и достаточные условия для того, чтобы спектр оператора ![]() совпадал с множеством
совпадал с множеством ![]() . А связь между числовым образом и спектром модели Фридрихса с двумерным возмущением изучена в работе [6].
. А связь между числовым образом и спектром модели Фридрихса с двумерным возмущением изучена в работе [6].
Литература:
- O.Toeplitz. Das algebraische Analogon zu einem Satze von Fejer. Math. Z., 1918, vol. 2, no. 1–2, pp. 187–197.
- H.Langer, C.Tretter. Spectral decomposition of some nonselfadjoint block operator matrices. J. Operator Theory, 39:2 (1998), 339–359.
- H.Langer, A. S. Markus, V. I. Matsaev, C.Tretter. A new concept for block operator matrices: the quadratic numerical range. Linear Algebra Appl., 330:1–3 (2001), 89–112.
- H.Langer, A. S. Markus, C.Tretter. Corners of numerical ranges. In Recent advances in operator theory (Groningen, 1998), vol. 124 of Oper. Theory Adv. Appl., 385–400 (Birkhauser, Basel, 2001).
- Т. Х. Расулов, Э. Б. Дилмуродов. Исследование числовой области значений одной операторной матрицы. Вестн. Сам. гост. техн. ун-та. Сер. Физ.-мат. науки, 2014. № 2(35). С. 50–63.
- Т. Х. Расулов, Э.Дилмуродов. Оценки для квадратичной числовой области значений одной операторной матрицы. Узбекский математический журнал. № 1 (2015), С. 64–74







