GeoGebra как средство решения стереометрических задач



В статье рассматривается применение возможностей программы GeoGebra решения стереометрических задач.

Математика одна из сложных наук, дающаяся ученикам не просто, ведь она требует достаточно хорошо развитого абстрактного мышления. Несмотря на сложность, овладение данной наукой вносит бесценный вклад в развитие человека. О важности и значимости математики говорит тот факт, что древние ученые, наряду с занятием философией, которую многие считают полной противоположностью точным наукам, занимались математикой, говоря о том, что «она приводит в порядок ум и мысли». Поэтому школьное образование, ставящее перед собой цель развития всесторонне развитой личности, отводит математике особое место.

Глубокому усвоению всему школьному курсу математики способствует стереометрия, изучаемая в старших классах. Ведь решение стереометрической задачи чаще всего требует выделения плоскостных объектов в составе пространственных, а это приводит к необходимости решать ряд планиметрических задач. Таким образом, решая задачи по стереометрии, всё время приходится возвращаться к планиметрии, повторять теоремы и вспоминать различные формулы. При решении стереометрических задач ещё в большей мере, чем в планиметрии, используются средства алгебры и тригонометрии, применяются векторный и координатный методы, дифференцирование и интегрирование. Таким образом, задачи по стереометрии способствуют творческому овладению всей совокупностью математических знаний [1, с. 4].

Решение задачи, неважно какой сфере она принадлежит, начинается с её анализа: выделения условия (что дано) и вопроса (что найти/доказать). Если уже на первом этапе решения ученик не может правильно понять, что от него требуется, задача заведомо будет решена неверно. В стереометрических задачах сложность заключается в том, что именно первый этап зачастую вызывает затруднения у учеников, поскольку требует проявления способности абстрактно мыслить, позволяющей правильно понять условие задачи, представить и изобразить тело, данное по условию, и сообразить, что требуется найти/доказать. На данном этапе самое значимое место отводится рисунку. Ребёнку необходимо не только изобразить чертёж в тетради, но и правильно его прочитать, понять, что рисунок на бумаге не даёт полного представления об изучаемом теле и во многом является условным. Важно, чтобы ученик, глядя на плоский рисунок, мог вообразить это пространственное тело и выявить данные по условию задачи элементы. Для формирования представления геометрических тел на уроках можно использовать макеты, модели геометрических фигур, которые позволяют рассмотреть их со всех сторон и продемонстрировать на них некоторые свойства. Однако, при решении стереометрических задач они не всегда эффективны: на моделях нельзя ставить точки, проводить прямые, плоскости и т. д.

Сегодня есть альтернатива макетам геометрических тел в виде 3D моделей, созданных на компьютере. Существуют компьютерные технологии, позволяющие учителю не только демонстрировать объекты изучения, но и в некоторых случаях даже решать задачи. Одним из таких помощников является программа GeoGebra, которая обладает широким спектром возможностей работы со многими разделами математики. Она применима для демонстрации как алгебраических, так и геометрических понятий и законов.

Для решения задач по стереометрии, GeoGebra обладает некоторым инструментарием, позволяющим не только строить пространственные тела, производить с ними различные манипуляции (изменять точки привязки фигуры, наблюдая изменение формы тела, вращать и анимировать), но и находить расстояние между точками, точкой и прямой, рассчитывать величины углов. Таким образом, продукт, созданный в программе, можно использовать в качестве наглядного пособия для правильного истолкования условия задачи, а также в качестве одного из способов решения или проверки правильности решения.

Удобство применения среды GeoGebra рассмотрим на конкретной задаче, взятой из сборника для подготовки к единому государственному экзамену «ЕГЭ 2018. Тематический тренажёр. Математика. Профильный уровень: задания части 2» [2, с. 38].

Задача 10. 58

В правильной четырёхугольной пирамиде SABCD боковое ребро SA равно , а высота SH пирамиды равна .

Точки M и N — середины рёбер CD и AB соответственно, NT — высота пирамиды с вершиной N и основанием SCD.

а) Доказать, что точка T — середина отрезка SM.

Решение:

К данной задаче, в системе GeoGebra можно создать 3D-модель, причём, если использовать 3D-модель только в качестве наглядного пособия, то точное численное соблюдение всех значений величин пирамиды не требуется и достаточно просто с помощью средств данной программы изобразить пирамиду. Это можно делать во многих программах 3D-графики. Но как было заявлено выше, GeoGebra владеет некоторым инструментарием, позволяющим решать стереометрические задачи, в данном случае, программа позволяет проверить и показать, что действительно точка T, являющаяся основанием высоты, будет ещё и серединой отрезка SM.

Итак, чтобы решить данную задачу средствами GeoGebra, необходимо в первую очередь построить пирамиду SABCD и выделить в её составе пирамиду NSCD.

Переходим к построению правильной четырёхугольной пирамиды SABCD.

Пирамиду в GeoGebra можно построить разными способами, но удобней строить пирамиду по основанию и высоте, с помощью команды Пирамида (<Полигон>, <Высота>).

Начнем построение с основания пирамиды (построение основания удобно выполнять на полотне 2D, связанном с полотном 3D). Так как по условию пирамида правильная, следовательно, в основании лежит квадрат. Таким образом, для построения основания достаточно знать длину стороны квадрата ABCD.

Для проведения вычислений, построим вспомогательную пирамиду (рис. 1).

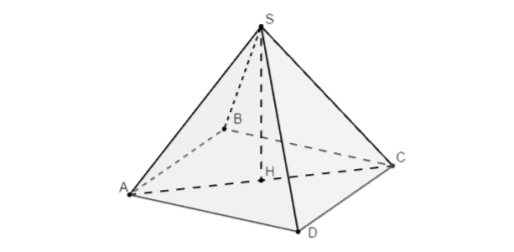
Рис. 1. Вспомогательный чертёж пирамиды SABCD

Вычислить длину стороны квадрата ABCD, обозначив её , не сложно:

, т.e.или.

В свою очередь, , а .

Таким образом,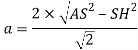, т. е. .

Построим основание пирамиды и обозначим его «многоугольник1». Сделать это можно следующим образом:

– либо отметим точки: A = (-1; -1; 0), B = (-1; 1; 0), C = (1; 1; 0), D = (1; -1; 0), затем соберём их в единый объект с помощью команды: многоугольник1 = (A, B, C, D);

– либо, так как пирамида правильная, с помощью инструмента «Правильный многоугольник», укажем две смежные вершины многоугольника A и B, и в появившемся диалоговом окне введём количество вершин — 4 (программа пропишет эту команду следующим образом: многоугольник1 = (A, B, 4)).

Высота имеет иррациональность в значении (), построить её не просто, так как в GeoGebra отрезок заданной длины не может быть иррациональным числом (программа автоматически такие значения округляет), а геометрия не терпит округлений. Поэтому для получения SH, выполним вспомогательные построения (для вспомогательных построений удобней использовать 2D полотно). Применяя теорему Пифагора, построим прямоугольный треугольник, катет которого будет иррациональным числом равным .

Представим числоследующим образом:.

Отметим на оси координат точки: О(0, 0), Q(1, 0). Построим прямую, перпендикулярную прямой OQ, с помощью соответствующего инструмента (прямая совпадает с осью ординат). Проведём окружность с центром в точке Q и радиусом 2 см, находим точку пересечения данной окружности и проведённой прямой. Получим отрезок OR, длина которого равна см (рис. 2).

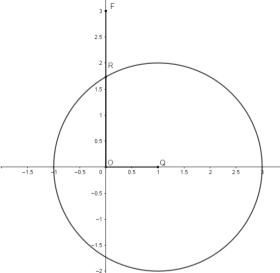
Рис. 2. Длина отрезка SH см

Построим пирамиду либо соответствующим инструментом, либо прописав команду: b = Пирамида (многоугольник1, OR) (рис. 3).

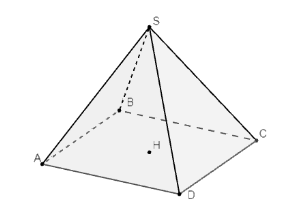
Рис. 3. Пирамида SABCD

Отметим точки M(1, 0, 0) и N(-1, 0, 0).

Выделим пирамиду NSCD, содержащуюся в пирамиде SABCD. Для этого введём в командной строке: d = Пирамида(N, D, S, C) (рис. 4).

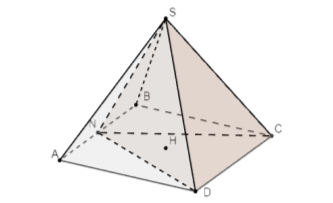
Рис. 4. Построение пирамиды NSCD

Так как пирамида NSCD содержится в пирамиде SABCD, то не каждый ученик, даже смотря на 3D модель, сможет сразу увидеть и понять её форму. Здесь на помощь приходит анимация, которую позволяет осуществить GeoGebra. Создадим анимацию, при которой из основной пирамиды SABCD, будет выезжать на указанный вектор (его определим сами) пирамида NSCD, в которой и нужно выяснить, куда падает высота NT.

Укажем произвольный вектор u. Удобно перемещать пирамиду по оси абсцисс, поэтому с помощью инструмента «Вектор» указываем вектор, началом которого будет являться точка A, а концом D, или вводим команду: u = Вектор (A, D).

Создадим на полотне 2D ползунок k, с помощью инструмента «Ползунок», ему зададим следующие параметры: интервал от 0 до 1.5, шаг — 0.001, скорость — 1, повтор — колебания.

Введём команду анимации: Перенести (d, Вектор (uk)), тем самым указав программе: при движении ползунка перемещать по оси абсцисс пирамиду NSCD на вектор uk. Работа программы продемонстрирована на рисунке 5.

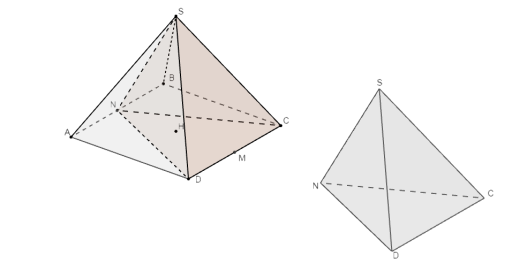
Рис. 5. Анимация выдвижения пирамиды NSDC

После демонстрации тела, с которым необходимо работать, вернёмся к условию задачи. Есть два способа решения:

1. Поэтапно-вычислительный метод решения задачи. Данный способ заключается в следующем: необходимо построить прямую, проходящую через точку N и T — середину SM и посмотреть, будет ли угол между этой прямой и плоскостью SDC равен 90.

В GeoGebra решение данным способ осуществляется следующим образом:

– построим отрезок SM с помощью соответствующей команды;

– отметим точку Т — середину SM с помощью соответствующего инструмента или команды: Т = Середина(S, M). Программа автоматически рассчитает координаты точки Т (0.5, 0, 0.87);

– построим луч NT, для этого используем соответствующий инструмент или команду: k = Луч (N, T);

– с помощью команды Угол (<Линия>, <Плоскость>) или соответствующего инструмента рассчитаем угол между NT и (SDC). Таким образом, команда примет вид: α = Угол (k, e). (При построении пирамиды, программа автоматически называет грани. Грань SDC обозначена е);

– после команды «Угол» программа автоматически обозначит на 3D модели искомый угол и подпишет его значение, так же в самой программе, после символа → появится значение угла, а именно 90 (рис. 6). Следовательно, луч NT перпендикулярен плоскости (SDС), т. е. является высотой пирамиды.

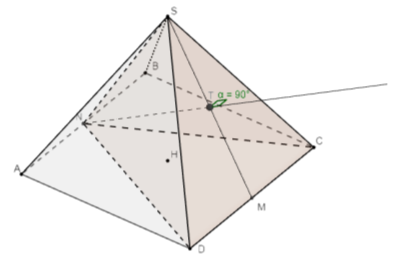
Рис. 6. Решение задачи поэтапно-вычислительным методом

2. Координатный метод решения задачи. Именно этот метод очень удобно использовать при решении задач в программе GeoGebra, так как при построении тел на 3D полотне автоматически задаётся система координат и в списке команд отображаются координаты точек, используемых при построении.

Для решения данной задачи этим способ необходимо найти координаты середины SM и координаты точки T, где NT — высота пирамиды NSDC и сравнить их. Если координаты равны, то точки совпадают.

Реализация решения задачи данным способом выглядит следующим образом:

– построим отрезок SM с помощью соответствующей команды;

– найдём координаты точки T — середины SM (как указано выше). В нашем случае T (0.5, 0, 0.87);

– построим перпендикуляр j из точки N на плоскость (SDC) с помощью команды: j = Перпендикуляр (N, e);

– найдём точку пересечения перпендикуляра j и плоскости (SDC) с помощью соответствующего инструмента или команды: К = Пересечение (j, e). Появляются координаты (0.5, 0, 0.87);

– координаты точки К будут посчитаны автоматически и как видно будут совпадать с координатами точки T, т. е. K = T. Так же в программе будет происходить наложение точки K на точку Т (рис. 7). Значит отрезок NT перпендикулярен плоскости SDC, а следовательно, является высотой пирамиды.

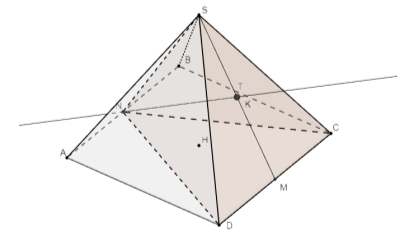
Рис. 7. Решение задачи координатным методом

Таким образом, GeoGebra не только представила 3D модель геометрического тела к задаче, но и позволила показать, что высота действительно падает в середину SM.

Нужно принять во внимание, что, если речь касается числовых вычислений, например, в задаче требуется найти длину отрезка, расстояние между точками, точкой и прямой, то если это значение будет иррациональным, GeoGebra, как отмечалось ранее, его округлит, тем самым ответ будет найден неверно. Данную ситуацию можно проследить на представленном выше примере: высота пирамиды SABCD равна и для точности построения высоты, выраженной иррациональным значением, были произведены дополнительные построения. При таком способе построения пирамиды SABCD значение рёбер должно быть равно . Если измерить длину рёбер, т. е. расстояние между вершиной S и точками A, B, C, D, инструментом «Расстояние», программа выведет значение равное 2.24, что является округлённым значением. Это же касается и тех случаев, когда нужно посчитать значение угла. Поэтому при построении нужно соблюдать точность, иначе при вычислении могут быть допущены ошибки.

Система компьютерной геометрии GeoGebra удобна и, что самое главное, универсальна в применении. Её можно успешно использовать для решения задач разного типа и уровня сложности.

Литература:

1. Готман Э. Г. Стереометрические задачи и методы их решения. — М.: МЦНМО, 2006. — 160 с..
2. Сергеев И. Н., Панферов В. С. ЕГЭ 2018. Тематический тренажёр. Математика. Профильный уровень: задания части 2 — М.: УЧПЕДГИЗ, 2018. — 94, [2] с. (Серия «ЕГЭ. Тематический тренажёр»)