В данной статье рассматривается пример использования обобщенно-регрессионной нейронной сети для прогнозирования результатов в индивидуальных видах спорта. Представлены данные экспериментов с использованием тестовой обучающей выборки, а также произведен анализ полученных данных. Представлены графики, характеризующие результаты, полученные в ходе экспериментов. Приведено описание работы обобщенно-регрессионной сети. Рассмотрена модель системы для прогнозирования спортивных результатов на основе нейронных сетей. Рассмотрены перспективы работы над системой прогнозирования.
Ключевые слова: нейронная сеть, нейрон, обобщенно-регрессионная нейронная сеть, спортивное прогнозирование, система, обучающая выборка, индивидуальные виды спорта, спортивный результат.
Спортивное прогнозирование предполагает предугадывание результатов предстоящих спортивных событий или контрольных результатов, которые спортсмен показывает на тренировке. Спортивное прогнозирование в индивидуальном виде спорта является прогнозированием результата или норматива спортсмена, не учитывая вероятностный коэффициент победы или поражения. Зная спрогнозированный контрольный или соревновательный результат, можно делать выводы о том, как построить тренировочные циклы, для физиологической подводки к прогнозу, теоретически возможно и предугадать место спортсмена, но на этом, в данной статье, подробно останавливаться не будем. Прогноз нейронной сети строится на основе обучающей выборки, которая в свою очередь включает в себя контрольные нормативы и показатели спортсмена, показанные им ранее. В такой обучающей выборке можно использовать данные о спортсмене показанные за несколько микро или макроциклов до момента, предполагаемого прогнозом. Спортивное прогнозирование — это популярное занятие в среде букмекеров, при этом в большинстве случаев все автоматизированные средства спортивного прогнозирования используют вероятностные математические модели, определяя при этом только вероятностный исход [1].
Существующие математические модели, для прогнозирования индивидуальных показателей спортсменов, редко используются в автоматизированных системах прогнозирования, а в случае индивидуального прогнозирования наиболее предпочтительны математические модели на основе методов многокритериального долгосрочного прогнозирования, применяемые в экономике и анализе телекоммуникационных сетей [2]. Для прогноза индивидуальных результатов необходимо учитывать весомый набор факторов, параметров, промежуточных тестовых показателей, погодных условий и даже информацию о фармакологических средствах, используемых спортсменом в процессе подготовки. Многообразны возможности ИТ-сферы для выбора средств прогнозирования, которыми могут являться системы прогнозирования на основе логического вывода [3], временные ряды, корреляционный анализ и системы на основе нейронных сетей (НС). Нейронные сети позволяет решить сложную задачу прогнозирования результата, основываясь на наборе факторов. Прогнозирование с помощью нейронных сетей достаточно распространённый метод, так как способность нейронной сети к прогнозированию напрямую следует из ее способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. Кроме того, НС решает проблему кластеризации больших объемов данных.
Студентами ВятГУ проводится работа по проектированию системы, предполагающей использование, для прогнозирования спортивных результатов в индивидуальных видах спорта, нейронных сетей, каждая из которых прогнозирует группу видов спорта, либо отдельные виды спорта [4]. Структура данной системы представлена на Рис. 1.
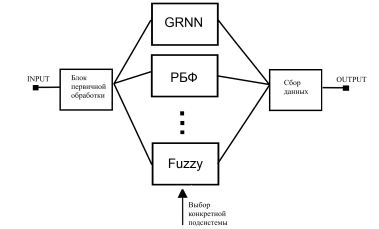
Рис. 1. Обобщенная структура системы для прогнозирования спортивных результатов
Обобщенно-регрессионная нейронная сеть (GRNN) устроена аналогично вероятностной нейронной сети (PNN), но она предназначена для решения задач регрессии, а не классификации. Как и в случае PNN-сети, в точку расположения каждого обучающего наблюдения помещается гауссова ядерная функция. Мы считаем, что каждое наблюдение свидетельствует о некоторой нашей уверенности в том, что поверхность отклика в данной точке имеет определенную высоту, и эта уверенность убывает при отходе в сторону от точки. GRNN-сеть копирует внутрь себя все обучающие наблюдения и использует их для оценки отклика в произвольной точке. Окончательная выходная оценка сети получается, как взвешенное среднее выходов по всем обучающим наблюдениям, где величины весов отражают расстояние от этих наблюдений до той точки, в которой производится оценивание (и, таким образом, более близкие точки вносят больший вклад в оценку) [5].
Обучающая выборка, составлена на основе имеющихся результатов за несколько тренировочных циклов мастера спорта в толкании ядра и содержит девять параметров и профильный, прогнозируемый, результат. Экспериментальные данные получены при использовании трех нейронных сетей, в том числе и обобщенно-регрессионной сети.
Обучающая выборка в экспериментах с GRNN имеет 345 векторов с девятью параметрами в каждом. График, построенный на основе обучающей выборки, представлен на Рис. 2.
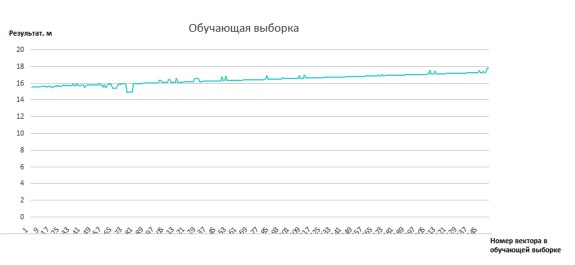
Рис. 2. График построенный на основе обучающей выборки
Сеть создавалась и обучалась в среде MathLab, график построенный после обучения нейронной сети на основе тестовых результатов представлен на Рис. 3.
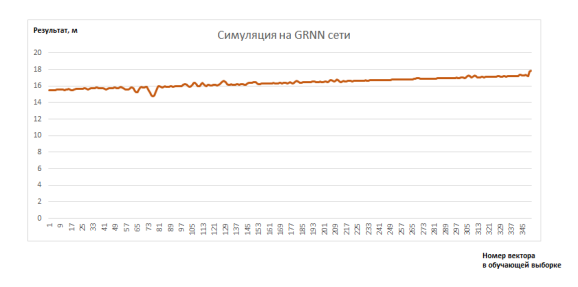
Рис. 3. График, построенный на основе тестовых результатов, полученных после обучения GRNN сети
Как видно их графика, сеть обучена. Часть результатов экспериментов с параметрами нейронной сети представлена в Табл. 1.
Таблица 1
Сравнение результатов обучения GRNN сети
|
GRNN, Целевая ошибка (GOAL) |
Ошибка обучения (MSE) |
|
0.0003 |
0.01e-11 |
|
0.003 |
0.116e-09 |
|
0.03 |
1.8997e-07 |
|
0.3 |
2.5471 |
|
3 |
29.4675 |
|
30 |
31.6274 |
|
300 |
31.6490 |
Специалистам, не имеющим представления о нейронных сетях, а также о той или иной спортивной сфере, может показаться, что такое прогнозирование решается очень просто, временным рядом или простой корреляцией, однако это не так. Ни временной ряд, ни корреляционная зависимость не решит такую проблему как падение результатов при высоких тестовых параметрах, неэффективности восстановительной фармакологии в определенные периоды и т. п. Для примера можно рассмотреть график (Рис. 4), где приведен фрагмент обучающей выборки и результатов уже обученной сети.
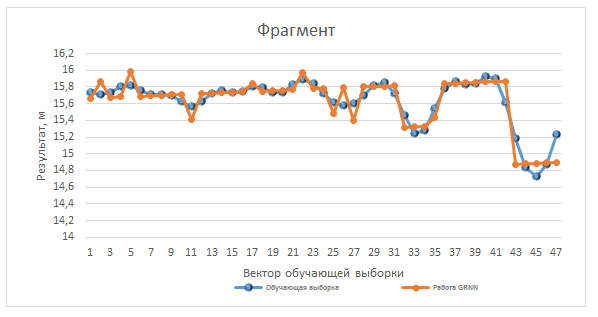
Рис. 4. Совмещенный график
Cеть использует свои способности к обобщению и обучается соответственно. Экранные формы работы данной сети в среде MathLab представлены на Рис. 5.
Рис. 5. Экранные формы
GRNN достаточно успешно проявила себя при прогнозировании результатов в дисциплине легкой атлетики — толкании ядра. Эта дисциплина относится к группе легкоатлетических метаний, которые достаточно близки друг к другу по ряду параметров общей и силовой подготовки, имеют близкие контрольные нормативы, за исключением специализированных упражнений и ряда технических параметров [6]. Поскольку представленная обучающая выборка имеет много общего с выборками, составленными по другим дисциплинам из группы легкоатлетических метаний (во всех легкоатлетических метаниях могут быть добавлены значения параметров спец. упражнений, значения погодных показателей), первично сделан вывод, о том, что GRNN-сеть подходит для достаточно точного прогнозирования результатов легкоатлетических метаний. Обученная сеть хранится в файле среды MathLab и доступна для работы и прогнозирования через стандартный интерфейс этой среды.
Литература:
- Прогнозирование исходов спортивных игр. URL: http://neuronus.com/stat/207-prognosys-sport-neural-claster.html. — (Дата обращения 20.10.2017).
- Усков А. А., Кузьмин А. В. Интеллектуальные технологии управления. –М.: Горячая линия Телеком, 2004. 143 с.
- Страбыкин Д. А. Метод логического прогнозирования развития ситуаций на основе абдуктивного вывода. Известия Российской академии наук. Теория и системы управления. 2013. № 5. С. 87.
- Крутиков А. К., Клюкин В. Л. Прогнозирование спортивных результатов с помощью нейронных сетей. Advanced Science. Технические науки. –ВятГУ, 2017, № 2. С. 44–52.
- Обобщенно-регрессионная нейронная сеть. URL: http://studbooks.net/2052401/informatika/obobschenno_regressionnaya_neyronnaya_set — (Дата обращения 11.03.2018)
- Бондарчук А. Управление тренировочным процессом спортсменов высокого класса. — М.: Олимпия Пресс, 2007, 272 с.







