В статье рассмотрен один из методов использования динамических рекуррентных искусственных нейронных сетей (ИНС) для решения прикладных задач оперативной диагностики оборудования, анализа, обучения и работы линейных (классических), гибридных, адаптивных и нечетких алгоритмов автоматического регулирования и управления. Показано, что от компактности и быстродействия работающих по шаговому принципу процессоров промышленных контроллеров зависят перспективы широкого внедрения нейросетевых технологий в промышленности. Предложен метод кодирования ИНС в сигнальные графы, и показано, что их матрицы смежности могут быть использованы в качестве ассоциативной памяти в шаговых матричных алгоритмах решения динамических рекуррентных ИНС. В статье изложена математическая постановка матричного метода решения рекуррентных ИНС. Показано, что в полносвязных рекуррентных ИНС любой нейрон может быть входным или выходным, причем один нейрон может одновременно быть входным и выходным. Приведены примеры обучения эволюционным алгоритмом оптимизации многоэкстремальных задач рекуррентных динамических ИНС предназначенных для идентификации динамических систем теплоэнергетических объектов. Функциями активационных блоков нейронов в динамических рекуррентных ИНС в настоящей работе использованы разностные выражения имитационных моделей линейных динамических звеньев. Показано, что для идентификации во временной области монотонных и колебательных переходных процессов в динамических системах третьего порядка удовлетворительная точность достигается на выходе любого нейрона рекуррентной динамической ИНС с четырьмя нейронами. При этом установлено, что полезная информация о динамических свойствах исследуемой динамической системы может быть одновременно получена с выхода любого нейрона сети.
Ключевые слова: искусственная нейронная сеть, синаптические веса, ассоциативная память, сигнальные графы, матрицы смежности сигнальных графов, шаговый алгоритм, динамическая рекуррентная нейронная сеть, линейный алгоритм регулирования, гибридный алгоритм регулирования, адаптивный алгоритм регулирования, нечеткий алгоритм регулирования, эволюционный алгоритм оптимизации многоэкстремальных задач, разностные выражения имитационных моделей линейных динамических звеньев контроллер, параметры объектов управления и регуляторов.
Сейчас в мире идет активное развитие перспективных технологий управления искусственного интеллекта, имитирующих природные процессы, такие как деятельность нейронов мозга. В прикладных задачах все большее распространение находят искусственные нейронные сети (ИНС) [1,2,3].
В определенном смысле являясь имитатором мозга ИНС обладает способностью к обучению и ориентации в условиях неопределенности. В процессе обучения она приобретает знания, которые сохраняются в ассоциативной памяти, во множестве значений коэффициентов межнейронных связей, называемых синаптическими весами (СВ).
По виду сигналов различают дискретные (импульсные) и аналоговые (непрерывные) ИНС. По функциональным возможностям ИНС находят применение в прикладных задачах оперативной диагностики и классификации состояния оборудования. Особым классом выделяются динамические ИНС/ Они находят применение в задачах идентификации объектов управления и синтезе линейных и нелинейных классических, гибридных, адаптивных и нечетких алгоритмов автоматического регулирования и управления [4]. От компактности и быстродействия алгоритмов их расчета в работающих по шаговому принципу процессорах промышленных контроллеров зависят перспективы широкого внедрения нейросетевых технологий в промышленности.
Существуют прямонаправленные и рекуррентные ИНС.
В настоящей работе топологию (внутренние связи) ИНС предлагается кодировать сигнальными графами [5]. Модель нейрона ИНС предлагается в сигнальном графе представлять узлом с присвоением ему порядкового номера 1, 2, …, N-1, N. Между собой узлы связаны направленными дугами. Дуги идентифицированы синаптическими весами wi,j, где i –номер нейрона-донора, j — номер нейрона-акцептора.
Для ИНС графы интересны своим матричным представлением. Удобным описателем ИНС является матрица смежности сигнального графа W. Элементы матриц смежности являются хранилищем ассоциативной памяти ИНС различного назначения.
На рис.1 показаны сигнальные графы и соответствующие им матрицы смежности: а) для прямонаправленной и б) рекуррентной ИНС. Из теории графов следует; если столбец матрицы смежности нулевой (рис.1а), то вершина сигнального графа является стоком, а в ИНС этот нейрон является входным. Нулевая строка показывает на вершину истока сигнального графа, а в ИНС этот нейрон является выходным. В рекуррентной ИНС (рис.1 б) нет формального понятия слоев. Любой нейрон может быть, как входным, так и выходным.
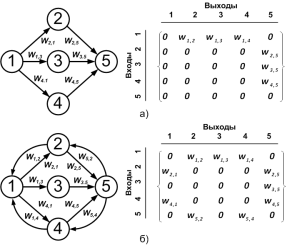
Рис. 1. Сигнальные графы и матрицы смежности: а) прямонаправленной и б) рекуррентной ИНС
Наиболее распространенными в настоящее время являются прямонаправленные ИНС, — персептроны [1]. В настоящее время в технике они широко используются для решения задач классификации состояния оборудования и диагностики событий. Для обучения прямонаправленных ИНС с большим числом нейронов имеется послойный метод обратного распространения [1].
Для моделирования и синтеза систем управления более привлекательными являются динамические рекуррентные ИНС (рис. 1 б).
Из-за внутрисетевых обратных связей для расчета каждого нейрона в рекуррентной ИНС требуются значения сигналов не только от связанных с ним выходов нейронов предыдущих слоев, как в прямонаправленных ИНС, но и значения сигналов, полученных на самом этом нейроне, и других, связанных с ним нейронов. Послойный расчет рекуррентных ИНС становится невозможен. В них каждый нейрон может быть одновременно и входным и выходным. В настоящее время нет формализованных алгоритмов расчета рекуррентных ИНС. Особенно это касается ИНС, предназначенных для моделирования динамических систем.
Известные из литературы алгоритмы имеют своей целью адаптацию алгоритма обратного распространения для расчета прямонаправленных ИНС с обратными связями [6]. Динамические свойства (ассоциативная память) в прямонаправленных ИНС достигается подачей входных сигналов на различные слои ИНС и увеличением общего числа нейронов.
Однако интуитивно просматривается аналогия с нейросетями существующих структур агрегатных и контроллерных алгоритмов регулирования. Причем в алгоритмах регулирования присутствуют реальные нелинейные элементы (аналоги активационных блоков). Но у них совсем небольшое число нейронов (функциональных блоков). Этим обусловлена необходимость, в отличие от многонейронных ИНС сканеров- классификаторов, изучения динамических ИНС с низу, от малого числа нейронов. А сложность их, топология и число нейронов, должны удовлетворять требования поставленным задачам, — качественной реализации различных видов классических, адаптивных, одноканальных и гибридных многоканальных, линейных с переключениями и нелинейных алгоритмов регулирования и логического управления.
Как показали исследования, перечисленные задачи могут быть реализованы динамическими рекуррентными ИНС, для которых в настоящее время нет формализованных алгоритмов расчета.
В настоящей статье предлагается матричный алгоритм численного шагового расчета рекуррентных ИНС.
В предлагаемом алгоритме модели нейронов ИНС представлены статическими уравнениями линейных сумматоров
![]() (1)
(1)
и активационного блока
В выражениях (1) и (2): ![]() — значения сигналов на входе n-го нейрона;
— значения сигналов на входе n-го нейрона; ![]() - СВ каналов на входе n-го нейрона;
- СВ каналов на входе n-го нейрона; ![]() - значение сигнала на выходе сумматора на k-ом шаге расчета ИНС;
- значение сигнала на выходе сумматора на k-ом шаге расчета ИНС; ![]() — функция преобразования активационного блока n-го нейрона;
— функция преобразования активационного блока n-го нейрона; ![]() — сигнал на выходе n-го нейрона на k-ом шаге расчета ИНС.
— сигнал на выходе n-го нейрона на k-ом шаге расчета ИНС.
В процессах обучения или работы ИНС предлагаемый матричный алгоритм требует:
‒ заполненную значениями СВ матрицу смежности сигнального графа ИНС W;
‒ вектор функций активационных блоков ![]()
![]() ; (3)
; (3)
‒ — вектор значений, подаваемых на входы всех нейронов ИНС внешних сигналов ![]()
![]() ; (4)
; (4)
‒ — вектор значений сигналов на выходах активационных блоков
![]() . (5)
. (5)
В процессе расчета ИНС элементы векторов ![]() и
и ![]() от шага к шагу изменяются. Допустим на k — ом шаге они имеют значения
от шага к шагу изменяются. Допустим на k — ом шаге они имеют значения ![]() и
и ![]() . Тогда сигналы, которые на k-ом шаге должны быть поданы на входы всех нейронов складываются из векторов
. Тогда сигналы, которые на k-ом шаге должны быть поданы на входы всех нейронов складываются из векторов ![]() и
и ![]()
Процедура вычисления сигнала на выходе сумматора j-го нейрона ИНС в соответствии с выражением (1) состоит в умножении элементов столбцов матрицы смежности W на элементы вектора ![]() с последующим суммированием результатов умножения с элементами j-го столбца этой матрицы.
с последующим суммированием результатов умножения с элементами j-го столбца этой матрицы.
А вектор сигналов на выходах нейронов на k — ом шаге вычисления получается в результате преобразования элементов вектора S функциями активационных блоков (2).
Если транспонировать матрицу смежности W, то процедура перемножения элементов строки матрицы WT на элементы вектора ![]() с последующим суммированием элементов полученных строк является формальной процедурой перемножения матрицы с вектором.
с последующим суммированием элементов полученных строк является формальной процедурой перемножения матрицы с вектором.
Из сказанного следует, что на k-м шаге процедура расчета ИНС сводится к трем этапам вычислений.
На первом этапе по значениям входных сигналов ![]() и результатам расчета ИНС на k-1 — ом шаге
и результатам расчета ИНС на k-1 — ом шаге ![]() , из выражения (5) вычисляются элементы вектора фактических входов нейронов ИНС для k-го шага
, из выражения (5) вычисляются элементы вектора фактических входов нейронов ИНС для k-го шага ![]() :
:
![]() . (7)
. (7)
На втором этапе производится умножение транспонированной матрицы смежности WT на вектор ![]()
![]() . (8)
. (8)
На третьем этапе после преобразования элементов вектора функциями активационных блоков (3)
![]() (9)
(9)
для k — го шага вычисляются элементы вектора сигналов на выходах нейронов ИНС
![]() . (10)
. (10)
Затем алгоритм возвращается к выполнению первого этапа для вычисления значений сигналов на выходах нейронов на k+1 — ом шаге работы ИНС.
Ниже показаны результаты испытания предлагаемого матричного алгоритма для расчета полносвязной динамической рекуррентной ИНС. На рис. 2 показаны графы четырех полносвязных рекуррентных ИНС.
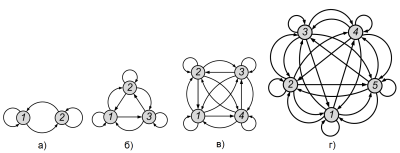
Рис. 2. Сигнальные графы четырех полносвязных рекуррентных ИНС
Топология полносвязных ИНС интересна максимальным интеллектом при обучении. Она хорошо формализована и удобна для алгоритмизации матричных операций преобразования выражений (7), (8), (9) и (10).
В матричном виде эти вычисления удобны потому, что у полносвязной рекуррентной ИНС число СВ равно квадрату от числа нейронов, а в сети любой нейрон, включая входной, может быть использован как выходной.
Для динамических ИНС, ориентированных для работы в системах регулирования и управления важными свойством является их инерционность.
В предлагаемом шаговом алгоритме для вычисления элементов вектора Г на текущем, k-ом шаге требуются значения на выходах всех нейронов на предыдущем (k — 1)-ом шаге. Тогда, если приращение значения сигнала на выходе n-ого нейрона от шага к шагу
![]() (11)
(11)
помножить на принятый интервал времени между шагами расчетов
![]() , (12)
, (12)
то в нейроне будет воспроизведена операция интегрирования примитива имитационной динамической модели нейрона с N входами
![]() (13)
(13)
При этом размер шага (интервал времени между расчетами t) будет определять точность моделирования переходных процессов. Тогда элементы вектора Г будут стековым хранилищем ассоциативной памяти динамической ИНС.
В качестве активационных блоков в предлагаемом алгоритме испытаны упрощенные примитивы рекуррентных выражений с единичными параметрами одномерных имитационных моделей линейного интегрального звена
![]() , (14)
, (14)
и линейного инерционного (апериодического) звена
![]() . (15)
. (15)
Для сравнения алгоритм испытан с функцией сигмоид в качестве активационного блока
![]() .(16)
.(16)
Получено, что выражения (14) и (15) практически одинаково положительно влияют на динамические свойства обучаемой ИНС, а с выражением (16) не удалось обучить ИНС на динамический режим работы. Очевидно, сигмоид применим только для ИНС классификаторов.
Нейросеть обучалась в режиме идентификатора по тестовым графикам реакции объекта на ступенчатое воздействие и на гармонические колебания одинаковой амплитуды на трех частотах. Тестовые сигналы генерировались схемой из рекуррентных выражений последовательного соединения имитационных моделей апериодических звеньев (А-звеньев) с параметрами
Та = 10 с и ka = 3 ед.вых/ед.вх.
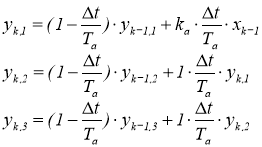 , (17)
, (17)
и схемой из рекуррентных выражений последовательного соединения А-звена и интегрирующего (И-звена) с отрицательной обратной связью
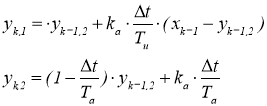 . (18)
. (18)
В системе (18) параметры А-звена Та = 10 с и ka = 3 ед.вых/ед.вх., а для И-звена ИНС обучена для двух вариантов: Ти = 50 с, когда переходный процесс монотонный, и Ти = 3 с, когда переходный процесс колебательный.
Инструментом для настройки ИНС в настоящей работе использован вероятностный эволюционный алгоритм оптимизации многоэкстремальных задач. Алгоритм состоит из вероятностной процедуры Монте-Карло для создания множества (популяции) начальных точек для поиска оптимального решения ![]()
![]() , где Z заданное число, генетической процедуры элиминации (удаления) 10 % неперспективных точек из множества R, операции восполнения множества R новыми, случайно выбранными точками и распределения их регулярным алгоритмом оптимизации по координатам локальных экстремумов. Алгоритм авторская разработка. Его описание опубликовано в [7], а программа зарегистрирована в фонде программ [8].
, где Z заданное число, генетической процедуры элиминации (удаления) 10 % неперспективных точек из множества R, операции восполнения множества R новыми, случайно выбранными точками и распределения их регулярным алгоритмом оптимизации по координатам локальных экстремумов. Алгоритм авторская разработка. Его описание опубликовано в [7], а программа зарегистрирована в фонде программ [8].
Вышерассмотренным эволюционным алгоритмом обучены полносвязные рекуррентные ИНС с двумя, тремя и четырьмя нейронами. Для всех вариантов задавалось одинаковая мощность множества начальных точек µ = 600, а критерием выхода из решения была принята допустимая разница между минимальным и максимальным значениями оптимизируемой функции ![]() . Расчеты производились на ПЭВМ с 3,1 GHz, 2 ГБ ОЗУ и с 64- разрядной операционной системой.
. Расчеты производились на ПЭВМ с 3,1 GHz, 2 ГБ ОЗУ и с 64- разрядной операционной системой.
На рис. 3 показаны результаты работы программы оптимизации; матрицы смежности с оптимальными значениями СВ для ИНС: а) с двумя, б) с тремя и в) с четырьмя нейронами.

Рис. 3. Матрицы смежности синаптических весов для рекуррентных ИНС: а) с двумя, б) с тремя и в) с четырьмя нейронами
Для обучения ИНС с четырьмя нейронами (поиска 16 значений СВ для матрицы в) на рис.3) программа затрачивает от 4 до 6 минут.
На рис. 4,5 и 6 показаны графики результатов исследования процессов обучения ИНС: а) с двумя, б) с тремя и в) с четырьмя нейронами. Видно, что точность идентификации зависит от числа нейронов, а динамическая погрешность ИНС зависит от скорости изменения моделируемого процесса.
Динамическая ошибка моделирования переходных процессов не более 10–3 ед. достигается ИНС в тремя нейронами.
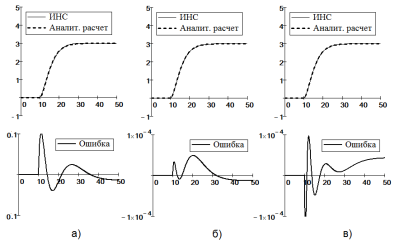
Рис. 4. Графики результатов обучения динамических рекуррентных ИНС на идентификацию системы (17)
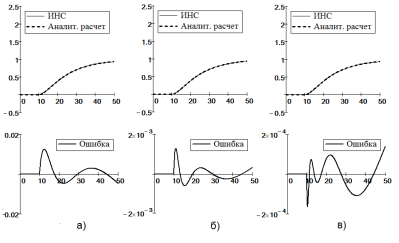
Рис. 5. Графики результатов обучения динамических рекуррентных ИНС на идентификацию системы (18) с параметрами А-звена Та = 10 с и ka= 3 ед. вых./ед. вх. и И-звена: Ти = 50 с
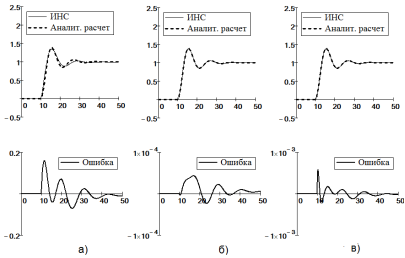
Рис. 6. Графики результатов обучения динамических рекуррентных ИНС на идентификацию системы (18) с параметрами А-звена Та = 10 с и ka = 3 ед. вых./ед. вх. и И-звена: Ти = 3
На рис. 7 и 8 показаны графики результатов исследования процессов обучения динамических рекуррентных ИНС с четырьмя нейронами на идентификацию переходного процесса на выходе: а) первого, б) второго и в) третьего нейронов для монотонных и колебательных переходных процессов.
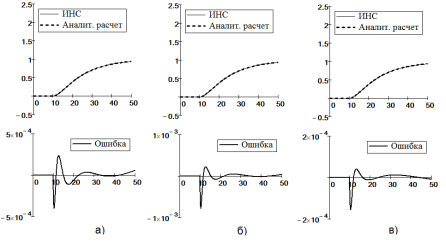
Рис. 7. Графики результатов исследования процессов обучения динамических рекуррентных ИНС с четырьмя нейронами на идентификацию переходного процесса на выходе: а) первого, б) второго и в) третьего нейронов для монотонных переходных процессов системе (18) с параметрами А-звена Та = 10 с и ka= 3 ед. вых./ед. вх. и И-звена: Ти = 50 с
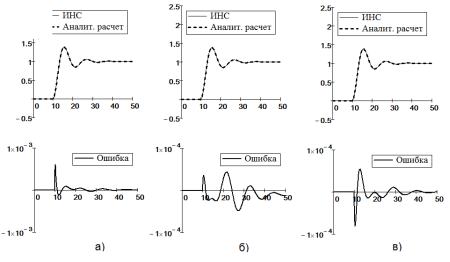
Рис. 8. Графики результатов исследования процессов обучения динамических рекуррентных ИНС с четырьмя нейронами на идентификацию переходного процесса на выходе: а) первого, б) второго и в) третьего нейронов для переходных процессов системе (18) с колебаниями с параметрами А-звена: Та = 10 с и ka= 3 ед. вых./ед. вх. и И-звена: Ти = 3 с
В работе сделано тестирование ИНС с четырьмя нейронами на идентификацию графиков при различных ступенчатых возмущениях. На рис. 9 показаны результаты тестирования при возмущениях: а) 0,5; б) 1,0 и в) 2.0 ед. Видно хорошее совпадение ИНС с аналитическими расчетами с удовлетворительной погрешностью.
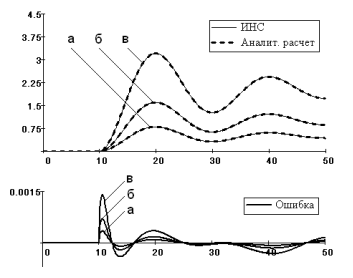
Рис. 9. Графики переходных процессов и динамических ошибок идентификации динамической системы (18) рекуррентной ИНС при ступенчатых возмущениях: а) 0,5; б) 1,0 и в) 2 ед.
На рис. 10 показаны ИНС и графики переходных процессов, полученных на выходах всех нейронов, полученных после обучения ИНС на идентификацию переходных процессов на выходе четвертого нейрона.
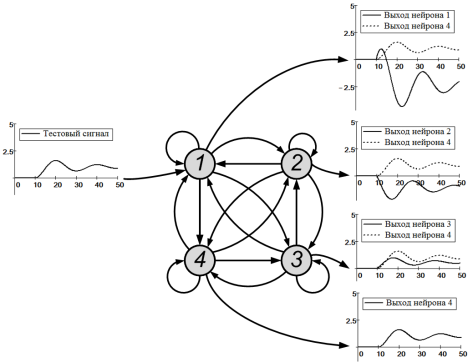
Рис. 10. Сигнальный граф рекуррентной ИНС обученной на идентификацию переходного процесса на выходе четвертого нейрона и графики переходных процессов на выходах остальных нейронов
Выводы
- В работе рассмотрены некоторые проблемы внедрения перспективных нейросетевых технологий в распространенную в РФ технику для решения прикладных задач оперативной диагностики оборудования, анализа, обучения и работы линейных (классических), гибридных, адаптивных и нечетких алгоритмов автоматического регулирования и управления. Показано, что перспективы широкого внедрения нейросетевых технологий зависят от компактности программных модулей и быстродействия работающих по шаговому принципу нейросетей с небольшим числом нейронов.
- Для моделирования и реализации динамических систем в алгоритмах управления в работе предлагается динамическая рекуррентная ИНС. Для лучшего восприятия новой технологии специалистами по автоматизации предлагается ИНС кодировать сигнальными графами.
- Для расчета динамических рекуррентных ИНС предложен пошаговый матричный метод, использующий матрицу смежности сигнального графа в качестве хранилища ассоциативной памяти.
- Для внедрения в программы промышленных контроллеров в работе предлагаются полносвязные рекуррентные ИНС. Топология их имеет максимальный интеллект (максимальное число СВ). Они хорошо формализованы и удобны для алгоритмизации матричных вычислений. В полносвязной рекуррентной ИНС число СВ равно квадрату от числа нейронов, а любой нейрон в сети, включая входной, может быть использован как выходной.
- Испытания показали, что для идентификации динамической системы третьего порядка достаточно обучить полносвязную рекуррентную ИНС с четырьмя нейронами.
- Испытываемая ИНС обучалась на ступенчатый тестовый сигнал и на три гармоники с разными частотами. Обучение выполнено вероятностным эволюционным алгоритмом оптимизации многоэкстремальных задач. На ПЭВМ с 3,1 GHz, 2 ГБ ОЗУ и с 64- разрядной ОС обучение выполнялось за 4–6 минут.
- Испытания показали, что в ИНС обученной на выбранный (см. рис.10, четвертый) выходной нейрон, на выходах ее остальных нейронов наблюдаются динамически связанные с сигналом на четвертом нейроне активные сигналы. Требуется исследование для возможного использования этих свойств рекуррентных ИНС в качестве виртуальных промежуточных сигналов в динамических системах.
Литература:
- Ж. Л. Лорьер. Нейронные сети. Системы искусственного интеллекта/ Ж. Л. Лорьер. 1991 год. — 568 с.
- Автоматические системы регулирования на основе нейросетевых технологий // Сабанин В. Р., Смирнов Н. И., Репин А. И. Сборник трудов конференции Control 2003. МЭИ, 2003. С. 45–51.
- Управление и инноватика в теплоэнергетике: учебное пособие / А. В. Андрюшин, В. Р. Сабанин, Н. И. Смирнов, — М.: Издательский дом МЭИ, 2011, — 392 с. ил.
- Некоторые результаты использования искусственных нейронных сетей в качестве регулятора автоматической системы регулирования // Сабанин В. Р., Дементьев Д. А., Казьмирук И. Ю. Сборник трудов 26-й международной научно-технической конференции «Современные технологии в задачах управления, автоматики и обработки информации» г. Алушта, Крым, Россия 14–20 сентября 2017 г. С. 60–61.
- Харари Френк. Теория графов // Перев. с англ. и предисл. В. П. Козырева. Под ред. Г. П. Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с.
- Методология обучения рекуррентной искусственной нейронной сети с динамической стековой памятью// В. Б. Лила, Е. В. Пучков // Продукты и системы //Software & Systems, № 4 (108), 2014.
- Модифицированный генетический алгоритм для задач оптимизации и управления// В. Р. Сабанин, Н. И. Смирнов, А. И. Репин// Exponenta Pro. Математика в приложениях. 2004. № 3–4. С.78–85.
- Универсальная программа для оптимизации многоэкстремальных задач «Optim-MGA»// В. Р. Сабанин, Н. И. Смирнов, А. И. Репин//Свидетельство об официальной регистрации программы для ЭВМ № 2004610862, 2004 г.







