C развитием мелкого и среднего бизнеса, все чаще возникает потребность в получении тонкодисперсного продукта без примесей в небольших количествах, что особенно важно для химической (красители, растворимые минеральные удобрения, различные добавки и др.), фармацевтической, пищевой, строительной и других отраслей народного хозяйства.
Ходаков Г.С. [1-2], Шинкоренко С.Ф. [3-4] и ряд других исследователей установили, что эффективность удара с ростом дисперсности частиц уменьшается вследствие увеличения затрат энергии на разрушение вторичных структур (агломератов), возникающих в порошке. Порошок достаточно высокой дисперсности по отношению к внешнему воздействию ведет себя подобно вязкой жидкости. С увеличением удельной поверхности порошка число контактов в нем растет и, соответственно, повышается его сопротивление удару, поэтому раздавливание и истирание является наиболее соответствующими физике процесса сверхтонкого помола. Что можно реализовать в мельницах с деформируемыми рабочими камерами[5].
При деформировании основным свойством рабочей камеры является способность изменять свои размеры под действием нагрузки. Использование в качестве рабочего органа деформируемую рабочую камеру позволяет получить новый механизм воздействия на обрабатываемую среду. При этом изменение жесткости, степени и способа деформирования, способа установки корпуса дает возможность изменить характер воздействия на материал в зависимости от его свойства и требуемых условий проведения процесса. По степени деформирования рассматриваемые типы камер относятся к кинематически деформируемым.
Для организации раздавливающих и истирающих воздействий на частицы, измельчаемого материала, как наиболее целесообразных при помоле материала с предварительно деформируемой структурой необходимо объем рабочей камеры предложенных устройств «плотно» заполнять мелющими телами.
Задача о максимальном заполнении пространства мелющими телами (шарами) имеет множество решений [6-7]. Рассмотрим некоторые из них.
В одном слое одинаковые шары уложены “плотнейшим” образом, это если каждый шар окружают шесть шаров (рис. 1). Перпендикулярно слою через центры шаров проходят поворотные оси шестого порядка и шесть плоскостей симметрии. Точечная группа позиции шара 6m (рис. 1, а). Каждый шар окружают шесть лунок. Через центры лунок проходят оси третьего порядка и три плоскости симметрии. Точечная группа позиции лунки 3m. Центры шаров, образующие гексагональную сетку, обозначены буквой А (рис. 1, б). Проекции центров лунок на плоскость, образованную центрами шаров первого слоя, обозначены буквами В и С.
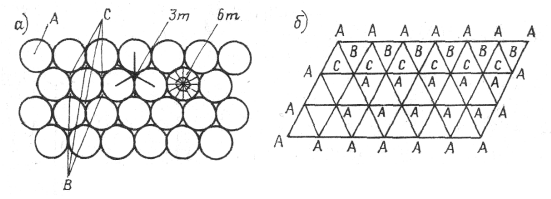
a – один плотноупакованный слой одинаковых шаров; б – центры шаров, образующие гексагональную сетку.
Рис. 1.
Следующий слой шаров образуется укладкой шаров в лунки между шарами нижнего слоя. Отметим, что шары второго слоя занимают лишь половину лунок, образованных шарами первого слоя. При этом центры шаров второго слоя будут располагаться либо над позициями В, либо над позициями С, но эти возможности равноценны.
Общими для двух слоев шаров останутся оси третьего порядка и плоскости симметрии. Во втором слое каждый шар окружают также шесть шаров и шесть лунок. При этом центры трех лунок во втором слое расположены над позициями А. Такие лунки А соответствуют несквозным отверстиям, находясь над центрами нижележащих шаров первого слоя. Центры других трех лунок находятся над позициями С. Такие лунки С соответствуют сквозным отверстиям, располагаются над лунками первого слоя. Укладку шаров третьего слоя можно осуществить двояким путем: помещая шары третьего слоя либо в несквозные лунки А, либо в сквозные С.
Пусть шары третьего слоя лежат в лунке типа А. Повторяя вышележащие слои шаров в указанном порядке, получим укладку шаров, которую обозначают как упаковку ...АВАВАВ.... В такой упаковке третий слой шаров повторяет первый, четвертый - второй и т.д. (рис. 2, а). Перпендикулярно слоям через центр шара проходят инверсионная ось шестого порядка и три плоскости симметрии. Точечная группа позиции шара 6m имеет гексагональную симметрию и называется “гексагональной упаковкой”.
Поскольку упаковка имеет периодическое строение, ее можно охарактеризовать элементарной ячейкой (рис. 2, б). В вершинах ячейки располагаются шары первого и третьего слоев, шар внутри ячейки принадлежит второму слою плотноупакованных шаров. Ближайшее расстояние между двумя шарами равно а, высота ячейки с. Высота элементарной ячейки с равна удвоенной высоте тетраэдра, образованного тремя шарами другого слоя. Поскольку сторона тетраэдра равна а, высота будет 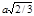 .
.
Итак, отношение 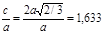 . В элементарной ячейке двухслойной упаковки слои шаров располагаются нормально направлению [00.1].
. В элементарной ячейке двухслойной упаковки слои шаров располагаются нормально направлению [00.1].
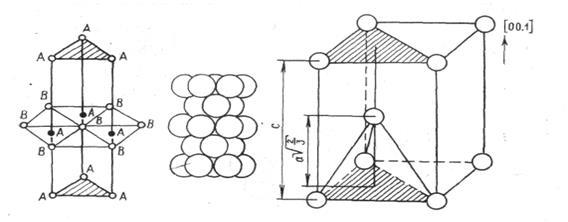
а) б)
а – двухслойная гексагональная упаковка; б – элементарная ячейка двухслойная гексагональная упаковка.
Рис. 2.
В гексагональной упаковке каждый шар в объеме окружен двенадцатью ближайшими соседями (рис. 3, а). Координационное число равно двенадцати. Однако часто для гексагональной упаковки указывают координационное число 6+(2´3). Такая запись подчеркивает тот факт, что в упаковке в ближайшем окружении любого шара имеются две симметрически независимые группы соседей: шесть шаров в слое и две тройки шаров в вышележащем и нижележащем слоях.
В гексагональной упаковке координационный многогранник имеет комбинированную форму и состоит из пинакоида и двух тригональных дипирамид (рис. 3, б). Такой многогранник называют гексагональным кубооктаэдром.
Рассмотрим иную укладку шаров третьего слоя. Пусть шары третьего слоя лежат в лунках типа С. Повторяя следующие слои в том же порядке, получим трехслойную укладку шаров, которую можно обозначить как упаковку ...АВСАВС... (рис. 4, а). В такой упаковке четвертый слой шаров повторяет первый, пятый - второй и т.д. Это трехслойная упаковка.
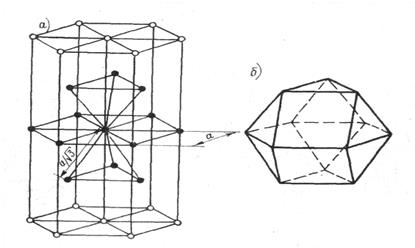
а – гексагональная упаковка с координационным числом равным двенадцати; б – координационный многогранник, состоящий из пинакоида и двух тригональных дипирамид.
Рис. 3.
По нормали слоям через центр шара проходят поворотная ось третьего порядка и три плоскости симметрии. Точечная группа позиции шара 3m. Такая укладка обладает периодичностью и, значит, ее можно охарактеризовать элементарной ячейкой. Это гранецентрированная кубическая ячейка (рис. 4, б). В элементарной ячейке трехслойной упаковки плотноупакованные слои шаров располагаются по нормали поворотной оси третьего порядка.
Особо следует подчеркнуть, что в трехслойной упаковке кроме плоскостей, используемых для построения упаковки, нормальных выбранному направлению, возникают еще три семейства таких плоскостей. Значит, плотнейшая упаковка имеет элементы симметрии, отличающиеся от элементов симметрии, перпендикулярных плоскости исходного слоя шаров.
Упаковки шаров можно характеризовать плотностью. Плотность выражают отношением объема шаров в элементарной ячейке к объему всей ячейки и выражают в процентах. Найдем плотность кубической упаковки шаров. Для этого выразим радиус шара R через ребро элементарной ячейки (рис. 4, б): 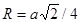 . Плотность упаковки -
. Плотность упаковки - 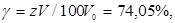 где V0 - объем ячейки (а3). Такую же плотность имеет гексагональная плотнейшая упаковка (рис. 5). Итак, шарами любых упаковок пространство заполняется на 74,05%. Немногим более четверти всего пространства принадлежит пустотам.
где V0 - объем ячейки (а3). Такую же плотность имеет гексагональная плотнейшая упаковка (рис. 5). Итак, шарами любых упаковок пространство заполняется на 74,05%. Немногим более четверти всего пространства принадлежит пустотам.
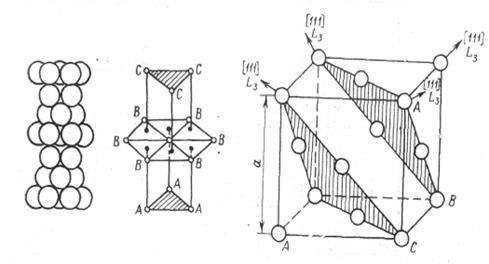
а) б)
а - плотнейшая трехслойная упаковка; б – гранецентрированная кубическая ячейка.
Рис. 4.
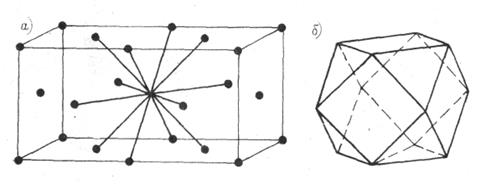
Рис. 5. - Гексагональная упаковка.
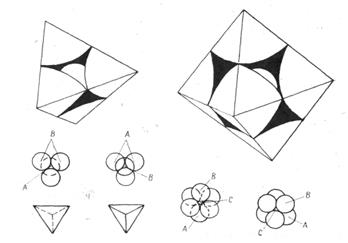
При укладке двух слоев шаров возникают пустоты двух видов. Одни из них называются тетраэдрическими (рис. 6, а), другие - октаэдрическими (рис. 6, б).
Тетраэдрическую пустоту образуют четыре шара. Если соединить центры этих шаров, получится тетраэдр (рис. 6, а). Центры тетраэдрических пустот располагаются над позициями А и В (рис. 1, б). Октаэдрическую пустоту образуют шесть шаров; если на центрах построить многогранник, получим октаэдр (рис. 6, б). Центры октаэдрических пустот располагаются над позициями С (рис. 1, а).
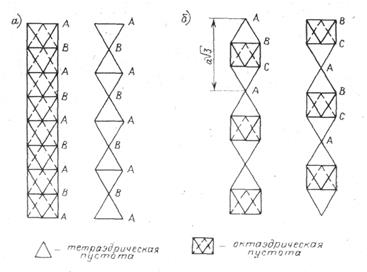
Чередование, взаимное расположение пустот в двухслойной и трехслойной упаковках шаров различно (рис. 7). Необходимо подчеркнуть, что в гексагональной упаковке (рис. 7, а) в отличие от кубической (рис. 7, б) имеются сквозные “люки”, образованные колонками октаэдрических пустот.
а) б)
а – тетраэдрический тип пустот между шарами; б – октаэдрический тип пустот между шарами.
Рис. 6.
а) б)
а – расположение пустот в двухслойной упаковке; б - расположение пустот в трехслойной упаковке.
Рис. 7.
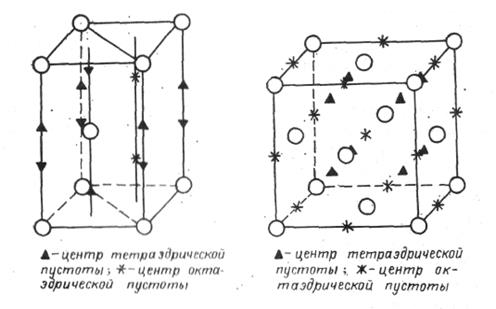
Элементарную ячейку трехслойной упаковки образуют четыре шара (8*1/8+6*1/2=4) (рис. 8, б). Ячейке полностью принадлежит восемь тетраэдрических и четыре октаэдрических пустоты. Центры тетраэдрических пустот совпадают с центрами восьми октантов.
Из четырех октаэдрических пустот одна располагается в центре ячейки. В середине каждого ребра ячейки также находится пустота. Таких пустот три (12*1/4=3). Соотношение числа пустот и шаров в трехслойной упаковке такое же, как и в двухслойной, т.к. соотношение между числом шаров и числом пустот можно выявить, сопоставляя окружение, с одной стороны, пустот шарами и, с другой, - шаров пустотами.
Любая октаэдрическая пустота составлена шестью шарами; любой шар “экспонируется” в шесть октаэдрических пустот (рис. 8, б), следовательно, число шаров и число октаэдрических пустот совпадает. Любая тетраэдрическая пустота составлена четырьмя шарами, любой шар “экспонируется” в восемь октаэдрических пустот вдвое больше числа шаров, поэтому число тетраэдрических пустот вдвое больше числа шаров. Это отношение числа шаров и пустот соответствует любой из рассмотренных упаковке шаров.
а) б)
а – элементарная ячейка гексагональной упаковки; б -элементарная ячейка трехслойной упаковки.
Рис. 8.
При помоле материалов интерес представляют не виды упаковок мелющих тел (шаров), а осуществляемые на их основе виды взаимодействий с частицами измельчаемого материала. Для реализации преимущественно раздавливающе-истирающих воздействий на измельчаемые частицы, камера должна быть плотно заполнена мелющими телами и материалом после ее деформирования, как видно из выше изложенного это есть совокупность кубической и гексагональной видов упаковок.
Библиографический список
1. Ходаков Г.С. Физика измельчения. - М.: Наука, 1972. - 307 с.
2. Ходаков Г.С. Тонкое измельчение строительных материалов. - М.: Стройиздат, 1972. - 239 с.
3. Шинкоренко С.В. Исследования в области теории и технологии измельчения руд (кинетика, моделирование интенсификация процессов):Автореф дисс. ...докт. техн. наук. - Днепропетровск , 1978. - 53 с.
4. Шинкоренко С.Ф. Технология измельчения руд черных металлов. - М.: Недра, 1983. - 213 с.
5. Лозовая С.Ю. Схемы мельниц с деформируемыми рабочими камерами. //Материалы международного конгресса «Современные технологии в промышленности строительных материалов и стройиндустрии», посвященного 150-летию В.Г.Шухова. - Белгород:БГТУ, 2003, Ч. IV. - С. 85-88.
6. Шаскольская М.П. Кристаллография. – М.: Высшая школа, 1984, 391 с.
7. Mizuno М., Fukaya А., JImbo G. Характеристика упаковки частиц при центробежном уплотнении тонкодисперсных порошков. // Funtai Kogaku Kaishi = of the Soc. of Powder Technology, Japan. - 1989. - Vol. 26, N 9. -P. 632-637.







