Использование матриц комбинаторного типа для построения разделяющей гиперплоскости в задачах кластеризации

Методы распознавания образов используются в различных прикладных областях. В результате сбора и первичной обработки данных формируются описания объектов или явлений. Далее возникает проблема классификации объектов, восстановления некоторых неизвестных значений их свойств, прогнозирования состояний.

Во многих задачах, где описания объектов задаются наборами значений числовых признаков (объекты суть точки n-мерного пространства), такие описания, принадлежащие разным классам, могут быть разделены поверхностями достаточно простого вида. Это есть принцип разделения. Простейший класс разделяющих поверхностей – гиперплоскости.

В реальном процессе распознавания нет полного перечня объектов, а имеется некоторые представители классов (априорная выборка). Возникает задача построения решающих функций и решающих правил на основе имеющейся выборки. Эти решающие функции определяются как меры близости новых объектов с имеющимися представителями каждого класса. Для детерминированных признаков чаще всего используются меры типа расстояние (метрика Хэмминга, евклидова метрика, метрика Минковского, взвешенная евклидова метрика).

Сформулируем проблему построения разделяющей гиперплоскости на примере разделения объектов двух классов.

Пусть, имеется w точек, заданных в пространстве Rⁿ, относящихся к двум различным классам K₁ и K₂: xⁱ Î K₁, i = 1, 2, …, k, y^j Î K₂, j=1, 2, …, l, w = k + l. Требуется построить гиперплоскость вида 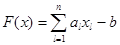, разделяющую два данных множества с учетом возможного отсутствия некоторых значений параметров в задании объектов.

Вообще говоря, для построения гиперплоскости, разделяющей объекты двух классов можно применить следующие рассуждения: если объект x принадлежит классу K₁, выполняется F(x) £ 0, если x Î K₂, то F(x) ³ 0), т.е. необходимо решить задачу нахождения коэффициентов a Î Rⁿ и b Î R таких, что

(a, xⁱ) £ b, i = 1, 2, …, k

(a, y^j) ³ b, j=1, 2, …, l

Таким образом, имеем систему, совместность которой говорит о существовании разделяющей гиперплоскости.

Опыт решения задач распознавания свидетельствует о том, что часто основная информация заключена не в отдельных признаках, а в их сочетаниях. К тому же не всегда известно, сочетание каких именно признаков информативно, а каких нет. Кроме того, на практике всегда имеются ограничения на ресурсы, на создание средств измерения признаков или ситуации отсутствия данных по некоторым из них. В связи с данной проблемой рассмотрим задачу построения решающего правила (разделяющей гиперплоскости), работающей как для всего признакового пространства, так и для отдельных его подпространств (которые, по сути, представляют собой наборы сочетаний признаков).

Рассмотрим первый объект, относящийся к классу K₁, во всевозможных подпространствах n-мерного пространства (всего их 2ⁿ – 1). Предположим, что при отсутствии измерений некоторых признаков, их значения полагаются равными нулю, что идентично операции проектирования на соответствующее подпространство. Будем формулировать задачу кластеризации таким образом, чтобы одно решающее правило работало во всех подпространствах признакового пространства, включая его самого. Тогда для отделения объекта необходимо решить относительно вектора a и числа b систему вида:

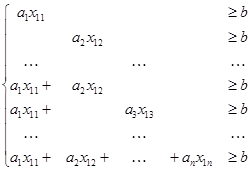        (1)

или в матричном виде:

Xa ³ b,

где a Î Rⁿ и b Î R, X Î R^m´n.

Матрица X имеет определенную структуру, запишем ее следующим образом: первые n строк матрицы содержат по 1 ненулевому элементу и представляют сочетание из n элементов по 1 или, что то же самое, подмножества множества {1, …, n} состоящие из одного элемента, следующие 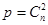 строк содержат по 2 элемента и являются подмножествами множества {1, …, n}, состоящими из двух элементов и т.д. Последняя строка содержит все n элементов. Очевидно, 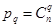, где q – число элементов в подмножестве. Таким образом, строки матрицы представляют наборы лексикографически упорядоченных подмножеств множества {1, …, n}.

Матрицу, элементы которой подчиняются такому принципу будем называть матрицей комбинаторного типа. Символом K_m,n будем обозначать множество всех вещественных матриц размера m ´ n, имеющих структуру комбинаторного типа.

В общем случае число ненулевых элементов матрицы комбинаторного типа равно
k = 2ⁿ×n / 2 = 2^n-1 × n, нулевых .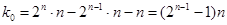

Построив для каждого объекта из представленной выборки систему вида (1), и применив описанные ранее рассуждения о построении разделяющей гиперплоскости, получим систему следующего вида:

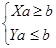,         (2)

где 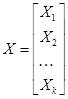, , 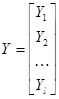X_i – матрицы комбинаторного типа, содержащие координаты i-го объекта класса K₁, Y_j – аналогичные матрицы для класса K₂. Необходимо найти коэффициенты a Î Rⁿ и b Î R такие, что система (2) является совместной.

Каждая матрица X_i, Y_j содержит в общем случае 2ⁿ-1 строк, следовательно, всего в системе (2) будет содержаться k (2ⁿ – 1) + l (2ⁿ – 1) = (k + l)(2ⁿ – 1) неравенств. Таким образом, имеем переопределенную систему линейных неравенств комбинаторного типа. В случае совместности данной системы, можно говорить о существовании гиперплоскости с заданными свойствами. Однако наиболее вероятным видится случай, когда подобная система неравенств будет противоречива (несовместна). Следовательно, имеет смысл говорить о постановке задачи коррекции, которая для произвольного общего случая формулируется в следующем виде.

Пусть имеется несобственная задача P (не имеющая решения в смысле данного определения). Эта задача погружается в класс P(x), являющийся параметризованным расширением исходной задачи. Область значений параметра x есть T, причем существует x₀ÎT такое, что P(x₀) º P, то есть совпадает с исходной задачей. Множество T значений параметра x разбивается на две области T =T₀ È T₁, T₀ Ç T₁ = Æ, такие, что при x Î T₀ задача P(x) – несобственная, а при x Î T₁ задача P(x) собственная (имеющая решение в смысле данного определения). Естественно предполагается, что класс P(x) выбран так, что T₁ ¹ Æ (очевидно, T₀ ¹ Æ, так как x₀ Î T₀). На классе P(x) вводится мера близости между его элементами (задачами). Достаточно определить «расстояние» между элементом P (то есть P(x₀)) и любым элементом P(x) при x Î T₁. Обозначив эту последнюю меру близости через j(x) = r(P, P(x)), задачу минимальной матричной коррекции модели (исходной задачи) можно сформулировать как нахождение значения параметра x₁ такого, что 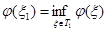. При этом P(x₁) будет коррекцией исходной задачи P.

В качестве меры близости j можно брать квадратичный критерий или максимальное по модулю значение параметра или другую метрику (псевдометрику).

В изучении проблемы коррекции несовместных систем линейных алгебраических уравнений получены серьезные результаты [1]-[5]. В последние годы особое внимание уделяется задачам структурной коррекции. В таких задачах система уравнений имеет матрицу определенной структуры (матрицы Теплица, блочные, разреженные матрицы), которую необходимо учитывать при коррекции [3], [4].

Рассмотрим задачу коррекции системы (2).

Задача 1. Пусть дана несовместная система (2), которую запишем в виде:

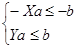    (3)

Необходимо найти матрицу 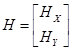размера (k + l)×(2ⁿ – 1) ´ n и вектор  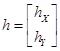размера (k + l)×(2ⁿ – 1), 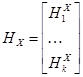, , 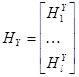, , 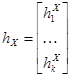, 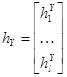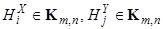такие, что система

                                                         

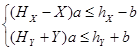
совместна и выполнено условие

.

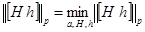Кроме того, в данной задаче имеем дополнительные ограничения на коррекцию: система (2) состоит из k + l блоков по 2ⁿ – 1 строк. В каждом блоке имеем матрицу комбинаторного типа (1), в столбцах которой находятся равные значения коэффициентов. Этому ограничению есть очевидное геометрическое объяснение: объекты выборки - суть точки n-мерного пространства, параметры (признаки) x_ij – координаты, очевидно, что каждая координата объекта определяется однозначно. Следовательно, в результате коррекции должны получить матрицу A + H с теми же свойствами (т.е. и матрица коррекции H должна соответствовать указанным ограничениям, которые примем как условия на коррекцию).

Решим данную задачу. Для начала приведем систему неравенств (3) к системе линейных уравнений с помощью стандартного перехода от ограничений-неравенств к равенствам:

                                                           .

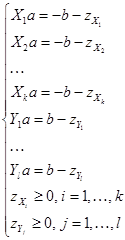Матрица H для данной системы примет вид:

                                           .

Для решения задачи 1, прежде всего понадобится провести процедуру параметризации матрицы комбинаторного типа H. Структура матрицы комбинаторного типа такова, что, зная размер матрицы m ´ n, по полученному в результате параметризации вектору a размерности k она может быть однозначно восстановлена. Данный факт позволяет в сформулированной задаче заменить понятие малости нормы матрицы на эквивалентное понятие – малость нормы вектора a, что в свою очередь дает возможность свести рассматриваемую задачу к задаче безусловной оптимизации.

Вообще говоря, вектор, параметризующий матрицу H(a) будет иметь размерность 2^n–1×n×w, a = [a₁, a₂, …, a_w]^T, где a_i – векторы, параметризующие соответственно матрицы H_i, H_j, i =1, …, k, j = 1, …, l, w = k + l. Однако с учетом ограничений, связанных с особенностями рассматриваемой задачи (каждая матрица X_i содержит k ненулевых элементов, n из которых различны), данное число можно значительно уменьшить:

" H_i, H_j, i =1, …, k, j = 1, …, l

                         .

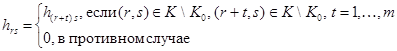Другими словами получаем матрицу вида

                                       .

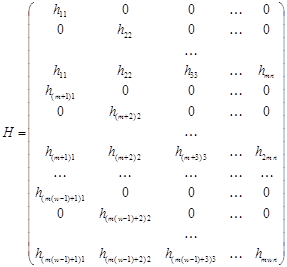Вектор a_i в таком случае может состоять из n×w элементов. Формирование индексов происходит по следующему принципу:

                                          

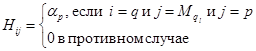
где p = 1, …, n×w, 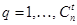, l = 1, …, t, t = 1, …, n, 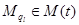, M(t) – множество всех подмножеств индексов j, состоящих из t элементов, упорядоченное в лексикографическом порядке.

Вектору a поставим в соответствие m ´ k матрицу A(a) следующим образом:

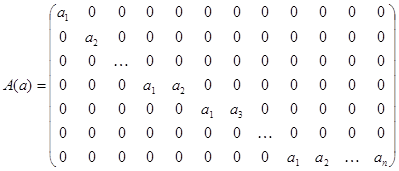
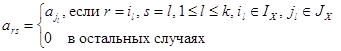
I_X={i: (i, j)ÎK\K₀}={i_l | l=1, …, k},

J_X={j: (i, j)ÎK\K₀}={j_l | l=1, …, k}

После проведенных преобразований можно применить алгоритм обобщенной наименьшей нормы [4] для решения задачи 1:

Вход: векторы a ÎR^k, b ÎR, e > 0.

Выход: векторы a_opt, z_opt, a_opt.

1.      Сформировать X(a) Î K_M,n.

2.      Положить x = x₀, z =z₀, сформировать A(a), r = - b – z - Xa.

3.      Повторять

                 

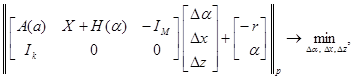
                  x = x + D x, a = a + Da, z_i = max(z_i + Dz_i, 0)

                  Сформировать H(a), A(a), r = (-b - z) - ( X + H )a

пока не выполнится ||Da, Dx, Dz||_¥ £ e.

a_opt = a, a_opt = a, z_opt = z.

 

Полученное решение позволит говорить о возможности минимального исправления положения объектов в признаковом пространстве таким образом, чтобы можно было провести разделяющую гиперплоскость, отделяющую объекты двух классов как во всем признаковом пространстве, так и в каждом из его подпространств.

 

Литература:

1.      Ватолин А.А. Несобственные задачи математического программирования и методы их коррекции: Дисс. на соиск. учен. степ. д-ра физ.-мат. наук: 01.01.09. - Екатеринбург, 1992.

2.      Горелик В.А., Ерохин В.И. Оптимальная матричная коррекция несовместных систем линейных алгебраических уравнений по минимуму евклидовой нормы. – М.: ВЦ РАН, 2004, 193 с.

3.      Горелик В.А., Ерохин В.И., Печенкин Р.В. Численные методы коррекции несобственных задач линейного программирования и структурных систем уравнений. – М.: ВЦ РАН, 2006, 150 с.

4.      Горелик В.А., Золтоева И.А., Печенкин Р.В. Методы коррекции несовместных линейных систем с разреженными матрицами. // Дискрет. анализ и исслед. операций, Сер. 2, 2007, Т. 14, № 2, С. 62-75.

5.      Горелик В.А., Муравьева О.В. Матричная коррекция данных в задачах оптимизации и классификации. // Моделирование, декомпозиция и оптимизация сложных динамических процессов. - М.: ВЦ РАН, 2004. С. 94 - 120.

6.      Журавлев Ю.И. Избранные научные труды. – М.: Магистр, 1998, 420 с.

7.      Горелик А.Л., Скрипкин В.А. Методы распознавания. – М.: Высш. шк., 2004. – 261 с.