Инженерно-техническое образование предусматривает серьезную графическую подготовку будущих специалистов, качество которой обеспечивается изучением в вузе таких общепрофессиональных дисциплин, как «Начертательная геометрия», «Инженерная графика», «Компьютерная графика», «Инженерная графика изделий машиностроения». Основной дисциплиной инженерного цикла является "Начертательная геометрия», которая способствует развитию пространственного воображения, творчески конструктивного мышления, а также воспитанию профессиональной и графической культуры обучающихся.
Содержание предмета «Начертательная геометрия» определяется специфически конкретными целями, а именно – научить студентов:
– способам изображения пространственных фигур на плоскости;
– мысленно воспроизводить пространственную форму изображенной на чертеже фигуры;
– решать графическим способом геометрические задачи, определяя позиционные, метрические и конструктивные характеристики изображенных на чертеже пространственных фигур и их совокупности.
В преподавании начертательной геометрии необходимо акцент делать на личностно-ориентированное направление в обучении, которое находит своё выражение в компетентностном подходе, понимаемом нами как единство теоретической и практической готовности студента к осуществлению трудовой творческо-конструкторской деятельности.
Реализация компетентностного подхода требует внедрения современных методов обучения, которые формируют профессиональную компетентность студентов как будущих специалистов, вооружают способами активизации знания, которое часто остаётся пассивным, то есть не находит практического применения [3]. При обучении начертательной геометрии на первом курсе, одним из таких методов является системный подход к обучению студентов.
Системный подход в изучении начертательной геометрии представляет собой некоторую особую методологическую (в широком смысле) установку, регулирующую направление выбора способов решений задач, а также теоретических и практических средств для изучения графических задач. При этом важно подчеркнуть следующее. Задачи, состоящие из большого числа подзадач или групп подзадач, должны рассматриваться в рамках одного типа задач (позиционные, метрические, аксонометрические и др.). Подход, сводящий по существу свойства элементов при решении сложных графических задач к свойствам целого, единого – демонстрирует свою эвристическую эффективность и носит название системного подхода.
Современные представления о системе позволяют выделить два подхода к пониманию системы [5]:
 |
Рисунок 1 – Два подхода к пониманию системы
С одной стороны это некоторый образ геометрических объектов, который отражает наши представления о предмете решения, является способом организации информации и служит целям познания, с другой стороны это некоторая конструкция, которая является инструментом решения задач и служит целям учебного процесса.
Система в начертательной геометрии определяется заданием системных объектов и связей между ними, представленных на рисунке 2.
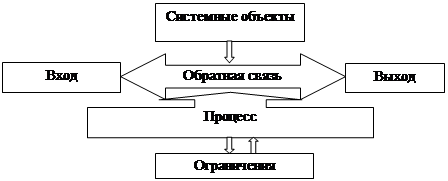 |
Рисунок 2 – Системные объекты и связи между ними
Вход – это то, что предшествует процессу усвоения дисциплины. Входом является информация на учебных занятиях. Во время протекания процесса усвоения материала входы могут меняться.
Любой процесс состоит из отдельных элементов, частей, операций и представляет собой динамичную систему взаимодействия различных факторов, явлений, подпроцессов. Под процессом при изучении начертательной геометрии понимаются следующие виды деятельности: лекции, практические, лабораторные занятия и др., преобразующие входы и выходы информации.
Следовательно, результат сложного процесса зависит от множества частных процессов. Поэтому выбор путей решения графических задач (вход) оказывается наиболее эффективным, если он осуществляется как системный процесс достижения необходимого результата (выхода).
Вход, выход и процесс системы являются ее главными элементами, позволяющими описывать систему. Систему, в зависимости от цели анализа, можно рассматривать в обоих направлениях – как от входа к выходу, так и от выхода к входу. Связь определяет последовательность процессов – выход данного процесса является входом другого определенного процесса, как на рисунке 3.
 |
|||
 |
|||
Рисунок 3 – Последовательность процессов
Позиционные задачи №1 (П.З. №1) – это задачи на принадлежность, по имеющимся проекциям точек, прямых находим недостающие проекции;
Позиционные задача №2 (П.З. №2) – это задачи на пересечение геометрических фигур, когда одна из них частного положения, одна из задач представлена на рисунке 3;
Позиционная задача № 3 (П.З. №3) – пересечение геометрических фигур общего положения.
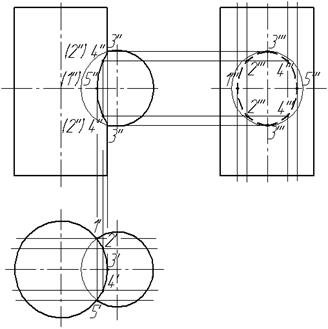
Рисунок 4 – Позиционная задача №2
Повеpхность цилиндpа, изобpаженная на pисунке 4, является гоpизонтально пpоециpующей, т. к. цилиндр перпендикулярен горизонтальной плоскости проекций (П1) значит на П1 уже есть одна из проекций линий пересечения – гоpизонтальная пpоекция линии пеpесечения совпадает с гоpизонтальной пpоекцией цилиндpа. Для нахождения второй проекции возвращаемся обратно, а именно к позиционной задаче № 1, фpонтальная пpоекция линии стpоится пpи помощи опpеделения pяда ее точек [2, с.35].
Применяя системный подход к решению графических задач, необходимо учитывать следующее:
– постановка задачи осуществляется с учетом главных элементов системы: входа, выхода и самого процесса решения задач;
– первоначальное генерирование идеи решения задач осуществляется с учетом достижения цели, остальные ограничения накладываются после генерирования идей;
– система должна иметь измеритель деятельности;
– критериями оценки вариантов решения является цель;
– для системы существует среда оказывающая влияние на эффективность деятельности системы и накладывающая дополнительные внешние ограничения;
– каждая задача должна рассматриваться как система в ее связях с другими задачами;
– при постановке и решении задач важно определить причинные факторы, от которых зависит решение задачи и новые проблемы, порождаемые решениями задачи;
– в процессе решения целесообразно сопоставлять промежуточные и окончательные результаты с выходными данными по цепи обратной связи, что позволяет процесс решения превратить в итеративный процесс постепенного улучшения решения;
В понятии системы можно выделить основные стороны:
1) состав системы – множество её элементов или частей. При изучении начертательной геометрии важно показать и дать четкое представление студентам о каждом элементе и каждой его позиции в начертательной геометрии;
2) структура системы – совокупность связей или отношений между частями. По мере овладения начертательной геометрией необходимо демонстрировать связь между задачами, постепенно переходя к более сложным задачам.
Например, чтобы построить изображение какого-нибудь предмета, (предметом называется неделимая совокупность геометрических тел и их частей между собой), необходимо обратиться сначала к первому этапу, затем к следующему и т. д. Только, пройдя все этапы, решение выстроится в стройную систему понятий и представлений, как на рисунке 5.
|
 |
||||
|
 |
||||
Рисунок 5 – Структура системы
3) сама система – то целое, которое образуется в результате соединения частей при помощи связей и не сводится к отдельным частям;
4) взаимодействие системы как целого с окружающей её средой, в котором проявляются свойства системы. Возникает необходимость показывать связь дисциплины с реальными производственными графическими задачами, результат деятельности – на производстве.
5) целевой характер системы или её связь с целью деятельности: цель определяет принцип отбора частей и связей, а значит, разным целям будут соответствовать разные системы. Например, качество подготовки специалистов влияет на их производственную деятельность [5].
Одним из главных направлений изучения начертательной геометрии с помощью системного подхода является формирование графического языка и системы понятий для теоретического и практического изучения курса.
Для освоения графического языка – языка техники в настоящее время необходимо наличие следующих условий [4]:
– развитое пространственное воображение, без которого невозможно никакое инженерное творчество;
– техническая эрудиция;
– знание правил оформления конструкторской документации;
– специальная подготовка по использованию вычислительной техники.
В обеспечении первого условия особую роль играет изучение начертательной геометрии, которая традиционно является теоретическим фундаментом инженерной графики. В начертательной геометрии изучаются основы построения и исследования геометрических моделей на базе методов графического отображения.
К следующим направлениям изучения начертательной геометрии с помощью системного подхода являются:
– разработка оптимальных способов решения задач;
– декомпозиция исходной системы на относительно обособленные части, для которых задачи начертательной геометрии становятся понятными;
– сведение нескольких понятий в одно, нескольких обособленных систем в одну – общую и разработка стратегии выбора решения задач и способа оценки состояния настоящей системы.
Относительно мышления системный подход выступает как способ организации процесса мышления, так как требует выполнения определенной последовательности действий. В большей мере это относится и к пространственному мышлению, без которого невозможно овладеть графическими дисциплинами.
В процессе реализации системного подхода при изучении начертательной геометрии задействованы все основные мыслительные операции в структуре пространственного мышления:
– анализ (расчленение на части);
– синтез (переход от частей к целому);
– сравнение (сопоставление целого и выявление взаимодействия);
– абстрагирование (выделение существенно важного с точки зрения цели);
– обобщение (переход от конкретных объектов к системе);
– конкретизация (движение от общего понятия системы к частной системе).
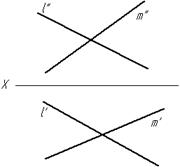
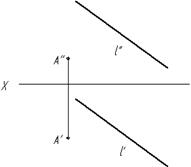
Рисунок 6 – Метрические задачи на определение расстояний
Например, решая метрические задачи, представленные на рисунке 6, используем все операции пространственного мышления [2, с.6-10].
Искомое расстояние во всех задачах этой группы измеряется длиной отрезка, заключенного между заданными геометрическими фигурами и перпендикулярного к одной из них или одновременно к обеим. Этот отрезок проецируется в конгруэнтный ему отрезок на плоскость проекций, которая будет перпендикулярна одной или обеим геометрическим фигурам, между которыми определяется расстояние. Отсюда вытекает общая схема решения задач этой группы:
Одним из способов преобразования комплексного чертежа привести обе заданные геометрические фигуры (или одну из них) в положение, перпендикулярное какой-либо
плоскости проекций. Построить проекцию искомого отрезка на эту плоскость.
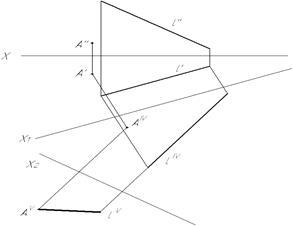
Рисунок 7 – Решение задачи на определение расстояния от точки А до прямой l
На основании этой схемы составляется алгоритм решения каждой конкретной задачи этой группы.
Выбирая способ преобразования комплексного чертежа при составлении алгоритма, следует исходить из требований компактности чертежа, четкости и простоты графических операций.
Системный подход выступает как средство упорядочения информации об объекте, потому что он представляет информацию в виде системы, включает систему в иерархию систем в качестве подсистемы и в качестве надсистемы. Это упорядочение играет важную роль в процессе обучения.
Системный подход не самоцель: в каждом конкретном случае его применение должно давать реальный, вполне ощутимый эффект [3].
При обучении начертательной геометрии необходимо:
– четко определять цели каждого вида работы (аудиторной – лекции, практические занятия, лабораторные работы, самостоятельной – выполнение расчетно-графических работ, решение задач в рабочих тетрадях);
– в соответствии с целями определять технологии обучения, которые соединяют методы, средства и формы обучения (применение прикладных компьютерных программ, изучение работы в графическом редакторе KOMPAS и классического решения задач (ручным способом);
– обучение студентов проводить с соблюдением логики умственного развития и достижения компетенций, вырабатываемых каждым студентом (использование многоуровневых тестовых заданий).
Основу выявления проблем системного характера, подготовки и принятия соответствующих решений при решении графических задач составляют такие типы мышлений: конструктивное образное, пространственное, ассоциативное, системное.
– конструктивное образное мышление – оно является универсальным средством применения знаний других предметных областей;
– пространственное мышление – способствует адекватному восприятию разнообразных форм окружающего мира;
– ассоциативное мышление – позволяет связать известный и понятный материал и на этой основе выявлять новые закономерности;
– системное – дает возможность обнаруживать связи между этапами решения задач, и, уясняя их подлинную природу и соответствующие закономерности, тем самым оказывать влияние на ход решения всей задачи.
Иными словами, системное мышление дает студенту инструмент для управления решениями графических задач.
В каждом конкретном случае такой ответственейший акт, как принятие решения, невозможно локализовать, как невозможно локализовать анализируемую систему и возникающую в ней проблему. Система может быть адекватно представлена только во взаимосвязях со своим окружением. Иначе говоря, объект анализа (в более широком контексте – познания) следует рассматривать как систему, существующую (функционирующую) в среде и взаимодействующую с другими системами. Лишь при таких условиях могут быть выявлены причины возникающей проблемы, источники и направления ее развития. И только на этой основе могут быть определены цели, способы и требуемые ресурсы для решения проблемы, то есть весь процесс решения проблемы должен быть систематизирован, технологичен, и только тогда может быть достигнут результат работы системного подхода.


 Изложение курса «Начертательная геометрия» с использованием системного подхода должно базироваться на следующих основных принципах, представленных на рисунке 8.
Изложение курса «Начертательная геометрия» с использованием системного подхода должно базироваться на следующих основных принципах, представленных на рисунке 8.
 |
 |
||||||
|
|
||||||
Рисунок 8 – Принципы изложения курса «Начертательная геометрия»
Системность предполагает использование системного подхода при решении как позиционных, так и метрических задач, что требует умения выделять в сколь угодно сложных системах элементы и отношения между ними, строить и исследовать модели систем, строить прогнозы развития систем и на их основе принимать и оценивать решения.
Принцип конкретности в процессе обучения означает следующее. Перед обучаемым, ставятся конкретные задачи из реальной практики решения пространственных задач, требующие привлечения соответствующих теоретических, методологических и методических материалов системного анализа для их решения. Это стимулирует студентов к опережающему обучению и развивает их способности к адаптации к незнакомым предметным областям.
Образность в процессе обучения достигается за счет использования современных графических, графоаналитических и модельных описаний изучаемых объектов, процессов и систем, введения в процесс обучения информационных систем, систем визуализации данных и различных графических пакетов. Это позволит повысить эффективность восприятия студентами учебного материала, развить их образное мышление, оснастить будущих специалистов новыми мощными средствами решения задач.
Информативный подход в процессе обучения реализуется за счет повышения "компьютерной" грамотности студентов первого курса и
Таким образом, для реализации системного подхода при изучении начертательной геометрии в техническом университете необходимо решать проблемы структуризации и иерархичности изучаемой дисциплины, выявляя закономерности и взаимосвязи с целью их более эффективного использования.
Задача преподавателей – научить студентов воспринимать причинно-следственные связи как некие нити, связывающие всё в окружающей его действительности. Тогда, выработав привычку к системному мышлению, они начинают видеть не просто отдельные части, а единое целое и взаимосвязанное, сами учатся осознанно и целенаправленно формировать обстоятельства, определять свои цели и задачи [1, с.56].
Особенности принятия системных решений заключаются в том, что основные усилия студента должны вкладываться в выявление и постановку проблемы, в ее формализацию, анализ, поиск множества альтернативных способов решения. Кроме того, отдельными важными моментами в творческой работе должно быть умение строить и исследовать модели предлагаемых задач, планировать и управлять на основе принимаемых решений, оценивать их последствия, внедрять новые информационные технологии.
Литература
1 Ботвинников, А.Д. Пути совершенствования методики обучения черчению / А. Д. Ботвинников. – М. : Просвещение, 1983. – 129 с.
2 Русинова, Л. П. Методические указания по решению метрических и позиционных задач для студентов 1 курса / Л. П. Русинова. – Сарапул, 2010. – 48 с.
3 Федотова, Н. В. Системный подход к изучению графических дисциплин в вузе / Н. В. Федотова, Г. В. Ханов // Успехи современного естествознания. – 2009. – №3. – Режим доступа : http://www.rae.ru.
4 Чопова, Н. В. Формирование профессиональных качеств будущего специалиста при обучении инженерной графике в вузе / Н. В. Чопова // Вестник ЦМО МГУ. – 2009. – №3. – Режим доступа : http://vestnik.cie.ru.
5 Шантаренко, В. Г. Системный подход к обучению студентов математике на основе моделирования в визуальном информационном поле как способ реализации когнитивно-визуального подхода / В. Г. Шантаренко // Вестник Омского государственного педагогического университета, 2007. – Режим доступа: http://www.omsk.edu.







