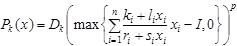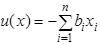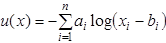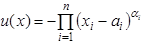В данной работе рассмотрены более распространенные функции полезности, каждая из которых исследовано численное решение задачи потребительского выбора с нелинейными ограничениями при модификации бюджетных ограничениях используя математический метод штрафных функций и учитывая разные виды штрафных функций.
In the given work were considered more well-known functions of utility, each of which the numerical solution of the consumer choice’s problem with nonlinear restrictions at updating budget restrictions is investigated using a mathematical method of penalty functions and considering different types of penalty functions.
Ключевые слова: теория потребления, функция полезности, штрафные функции, нелинейное программирование, метод штрафных функций, множество Парето.
Keywords: consumption theory, utility function, penalty functions, non-linear programming, penalty function method, Pareto set.
Считается, что потребитель располагает доходом I, который он полностью тратит на приобретение благ (продуктов). Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определенные количества благ, и математическая модель такого его поведения называется моделью потребительского выбора. На множестве потребительских наборов 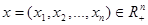 благ определена функция
благ определена функция 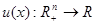 называемая функцией полезности потребителя, которой на потребительском наборе
называемая функцией полезности потребителя, которой на потребительском наборе 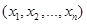 равно потребительской оценке индивидуума для этого набора.
равно потребительской оценке индивидуума для этого набора.
Функция полезности удовлетворяет следующим свойствам:
1) Возрастание потребления одного продукта при постоянном потреблении других продуктов ведет к росту потребительской оценки.
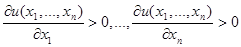
2) Предельная полезность (первая частная производная) каждого продукта уменьшается, если объем его потребления растет (это свойство предельной полезности называется законом убывания предельной полезности).
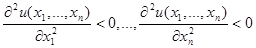
3) Предельная полезность каждого продукта увеличивается, если растут количества других продуктов.
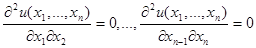
Линия, соединяющая потребительские наборы 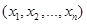 , имеющие один и тот же уровень удовлетворения потребностей индивидуума, называется линей безразличия. Линия безразличия есть не что иное, как линия уровня функции полезности.
, имеющие один и тот же уровень удовлетворения потребностей индивидуума, называется линей безразличия. Линия безразличия есть не что иное, как линия уровня функции полезности.
Задача потребительского выбора заключается в выборе такого потребительского набора 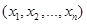 , который максимизирует его функцию полезности при заданном бюджетном ограничении. Задача потребительского выбора является задачей выпуклого программирования, так как функция полезности является выпуклой, то на бюджетном множестве существует единственная точка максимума функции полезности
, который максимизирует его функцию полезности при заданном бюджетном ограничении. Задача потребительского выбора является задачей выпуклого программирования, так как функция полезности является выпуклой, то на бюджетном множестве существует единственная точка максимума функции полезности
Бюджетное ограничение означает, денежные расходы на продукты не могут превышать денежного дохода, т.е. 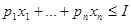 , где
, где 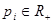 - рыночная цена одной единицы
- рыночная цена одной единицы 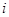 -го продукта, а
-го продукта, а 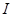 - доход индивидуума.
- доход индивидуума.
Пусть задана целевая функция полезности (предпочтения) потребителя 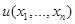 , где
, где 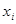 - количество
- количество 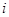 -го блага, вектор цен
-го блага, вектор цен 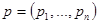 и доход
и доход 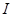 . Записав бюджетное ограничение и ограничения на неотрицательность, получаем задачу
. Записав бюджетное ограничение и ограничения на неотрицательность, получаем задачу
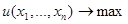
при условиях
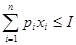
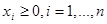
Для решения этой задачи на условный экстремум применим метод Лагранжа к задаче выпуклого программирования. Функция
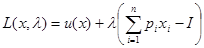
заданная на декартовом произведении 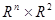 , называется функцией Лагранжа задачи потребительского выбора.
, называется функцией Лагранжа задачи потребительского выбора.
Выписываем необходимые условия экстремума:
а) условие стационарности
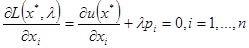
где 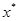 - точка локального экстремума в задаче потребительского выбора.
- точка локального экстремума в задаче потребительского выбора.
б) условие дополняющей нежесткости
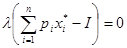
в) условие неотрицательности (согласования знаков)
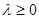
г) условие допустимости
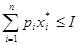
Из условия а) вытекает, что 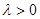 , в противном случае все предельные полезности были бы равными нулю и это влечет к противоречию свойства 1). Откуда следующая система уравнений
, в противном случае все предельные полезности были бы равными нулю и это влечет к противоречию свойства 1). Откуда следующая система уравнений
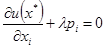
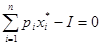
Отсюда вытекает, что для всех 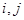 в точке
в точке 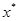 локального рыночного равновесия выполняется
локального рыночного равновесия выполняется
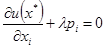
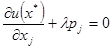
Исключив λ из этой системы, получаем следующее равенство
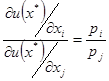
Итак, в точке оптимума отношение предельных полезностей любых двух благ равно отношению их рыночных цен.
Геометрически решение 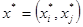 можно интерпретировать как точку касания линии безразличия (линии уровня) функции полезности
можно интерпретировать как точку касания линии безразличия (линии уровня) функции полезности 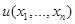 , с бюджетной прямой
, с бюджетной прямой 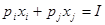 (см. рис. 1). Это определяется тем, что отношение
(см. рис. 1). Это определяется тем, что отношение 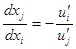 показывает тангенс угла наклона линии уровня функции полезности, а отношение
показывает тангенс угла наклона линии уровня функции полезности, а отношение 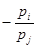 представляет тангенс угла наклона бюджетной прямой. Поскольку в точке потребительского выбора (или локального рыночного равновесия) они равны, в этой точке происходит касание данных двух линий.
представляет тангенс угла наклона бюджетной прямой. Поскольку в точке потребительского выбора (или локального рыночного равновесия) они равны, в этой точке происходит касание данных двух линий.
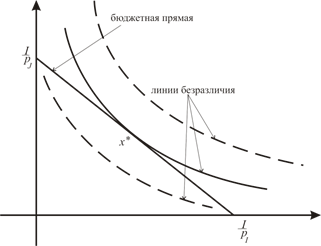
Рис.1
Задача
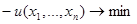 (1)
(1)
при условиях
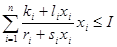 (2)
(2)
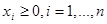 (3)
(3)
здесь 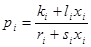 - функция, зависящая от
- функция, зависящая от 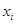 (количества благ
(количества благ 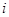 -го вида),
-го вида), 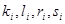 - числовые параметры, является двойственной задачей потребительского выбора с нелинейными ограничениями.
- числовые параметры, является двойственной задачей потребительского выбора с нелинейными ограничениями.
Основная задача метода штрафных функций состоит в преобразовании задачи минимизации функции 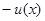 с соответствующими ограничениями, наложенными на
с соответствующими ограничениями, наложенными на 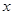 , в задачу поиска минимума без ограничений функции
, в задачу поиска минимума без ограничений функции 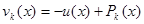 .
.
Функция 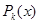 является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию
является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию 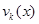 , т.е. увеличивала её значение. В этом случае минимум функции
, т.е. увеличивала её значение. В этом случае минимум функции 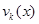 будет находиться внутри области ограничений.
будет находиться внутри области ограничений.
Методы штрафных функций разделяются на методы внутренней точки и методы внешней точки. Метод штрафных функций называется методом внутренней точки (внешней точки), если все точки последовательности 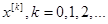 , являются допустимыми (недопустимыми). Вид метода (внутренней или внешней точки) определяет вид штрафной функции и правило, по которому производится пересчет штрафного параметра после решения очередной задачи безусловной минимизации.
, являются допустимыми (недопустимыми). Вид метода (внутренней или внешней точки) определяет вид штрафной функции и правило, по которому производится пересчет штрафного параметра после решения очередной задачи безусловной минимизации.
В качестве внутренней штрафной функции к (1)-(3) была рассмотрена следующая штрафная функция
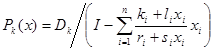 (4)
(4)
В качестве внешней штрафной функции была рассмотрена следующая штрафная функция
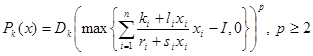 (5)
(5)
где 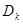 - коэффициенты штрафа (штрафные параметры),
- коэффициенты штрафа (штрафные параметры), 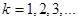
Тогда учитывая штрафную функцию (5), исходная задача потребительского выбора переходит к следующей задаче безусловного экстремума
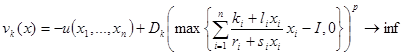
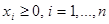
Алгоритм численного задачи условной минимизации методом штрафных функций заключается в следующем.
1. Задаются 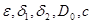 и
и 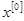 ; определяется
; определяется 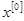 (внутренняя или внешняя); выбирается штрафная функция
(внутренняя или внешняя); выбирается штрафная функция 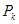 ; строится расширенная функция
; строится расширенная функция 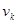 ; полагается
; полагается 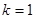 .
.
2. Решается одним из численных методов задача безусловной минимизации
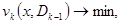
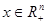 .
.
При этом начальная точка 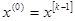 , условие окончания вычислений
, условие окончания вычислений
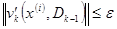 .
.
Результатом решения задачи безусловной минимизации является точка 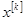 , в качестве которой используется оценка
, в качестве которой используется оценка 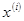 точки минимума задачи безусловной минимизации.
точки минимума задачи безусловной минимизации.
3. Проверяется условие при 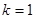 .
.
Если оно выполняется, то осуществляется переход к п. 5.
Если условие не выполняется, то осуществляется переход к п. 4.
4. Проверяются условия окончания решения исходной задачи:
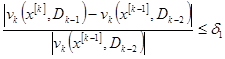
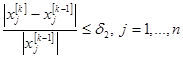 .
.
Если они выполняются, то полагается 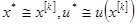 и вычисления завершаются.
и вычисления завершаются.
Если условия не выполняются, то осуществляется переход к п. 5.
5. Определяется 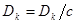 (в случае внутренней штрафной функции) и
(в случае внутренней штрафной функции) и 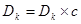 (в случае внешней), полагается
(в случае внешней), полагается 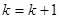 и осуществляется переход к п. 2.
и осуществляется переход к п. 2.
Для приведенного численного решения задачи потребительского выбора с нелинейными бюджетными ограничениями были рассмотрены следующие функции полезности:
1. функция полезности с полным взаимозамещением благ
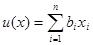
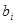 - числовая оценка полезности от потребителя единицы блага
- числовая оценка полезности от потребителя единицы блага 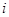 -го вида;
-го вида;
2. логарифмическая функция полезности
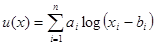
где 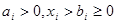 ;
;
3. функция полезности Стоуна
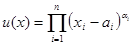
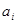 - минимально необходимое количество
- минимально необходимое количество 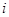 -го блага, которое приобретается при любом случае и не является предметом выбора, коэффициенты
-го блага, которое приобретается при любом случае и не является предметом выбора, коэффициенты 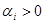 характеризуют относительную “ценность” благ для потребления.
характеризуют относительную “ценность” благ для потребления.
Ввод данных: размерность 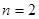 , параметры штрафной функции
, параметры штрафной функции 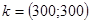 ,
, 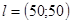 ,
, 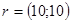 и
и 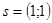 , бюджет потребителя
, бюджет потребителя 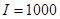 . Критерий останова
. Критерий останова
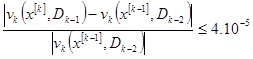 ,
, 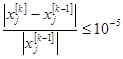 .
.
Результаты эксперимента отражены в таблице 1:
|
Функции полезности. |
Штрафные функции. |
|
|
|
|
|
|
|
-487,727322770006 |
-487,945044032733 |
|
|
-8,56921116125062 |
-8,5725068326183 |
|
|
-7,19309286473106 |
-7,19864290237822 |
Таблица 1. Результат минимизации 3-х функций полезности методом внутренних и внешних штрафных функций.
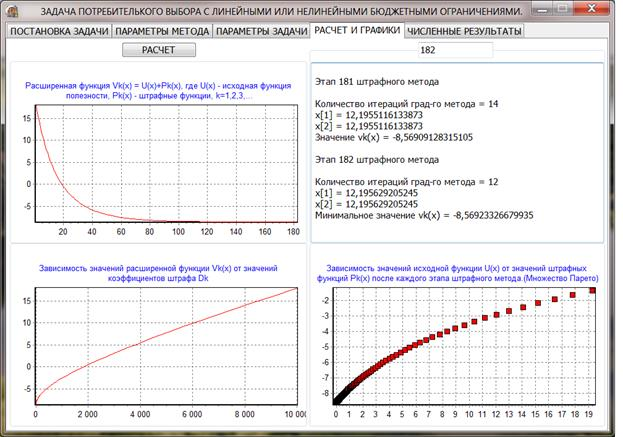
Компьютерное приложение, показывющее результат программы, написанной на языке delphi для исследования сходимости метода штрафных функций. Здесь показаны результаты эксперимента на функции Бернулли (логарифмическая функция полезности), преведены анализ зависимости значений расширенной функции от значений коэффициентов штрафа и анализ зависимости значений функции полезности Бернулли от значений штрафных функций после каждого этапа штрафного метода, т.е. строится множество Парето.
Литература:
1. Андреева Е. А., Цирулёва В. М. «Вариационное исчисление и методы оптимизации». – Тв. 2001.
2. Замков О. О., Толстопятенко А. В., Черемных Ю. Н. «Математические методы в экономике». – М. 2004.
3. Аллен Р. Математическая экономика. – М. Ил, 1963
4. Ашманов С.А. Введение в математическую экономику. – М.: Наука, 1984
5. Вагнер Г. Основы исследования операций. Тома I-III. –М.: Мир, 1972-73гг.
6. Гейл Д. Теория линейных экономических моделей. – М.: Ил, 1963
7. Джонстон Дж. Эконометрические методы. – М.: Статистика, 1980