Введение
Развитие мирового сообщества наглядно демонстрирует, что в последнее время критически важным государственным ресурсом, оказывающим все большее влияние на национальную безопасность, становится информация, циркулирующая в автоматизированных системах управления и связи. Ускоренное развитие информационных технологий открыло дополнительные возможности для преднамеренного деструктивного воздействия на них противостоящей стороны.
Во многих прикладных задачах необходимо знать ресурс, обеспечивающий отражение атаки противоборствующей стороны с заданной надежностью, примерами таких задач могут служить: оценка требуемой оснащенности правоохранительных органов для поддержания заданного уровня преступности; оценка численности защитников и их квалификации для поддержания уровня потерь организации от внешних и внутренних атак на ее ресурсы на приемлемом уровне; определение параметров устойчивости в обществе, состоящее из социальных групп с противоположными интересами. С целью решения этих и многих других задач разработан программно-аналитический комплекс по исследованию противоборства субъектов «Сфера» [1].
В связи с не возможностью использования статистических методов из-за отсутствия достаточных и достоверных материалов в области противоборства субъектов в основу программного комплекса положены теоретические методы исследования процессов противоборства субъектов в рамках направлений: теории игр, моделей противоборства субъектов с разными интересами (модели В.Вольтерра и их модификации), моделей сражения Ланкастера [2,3,4].
Программный комплекс является инструментом поддержки принятия решений аналитиков, занимающихся моделированием и исследованием процессов противоборства субъектов. С помощью данного инструмента можно производить анализ множества моделей противоборства субъектов, описанных по определенным правилам, удовлетворяющим архитектуре и логике работы программного комплекса, так же составлять прогноз состояния модели во времени.
Программный комплекс обеспечивает выполнение следующих функций:
- первичный ввод параметров математической модели противоборства субъектов;
- динамическое изменение параметров математической модели противоборства субъектов;
- решение систем дифференциальных уравнений, описывающих модели противоборства субъектов, численными методами (Рунге-Кутта, Рунге-Кутта-Адамса, Рунге-Кутта для уравнений Колмогорова) [5];
- построение фазовых портретов математических моделей противоборства субъектов с возможностью изменения скорости процесса расчета;
- построение серий фазовых портретов с изменяемым параметром;
- анализ устойчивости систем дифференциальных уравнений;
- построение графиков численностей противоборствующих субъектов;
- анализ результатов моделирования процессов противоборства субъектов;
- экспорт и импорт результатов исследуемых процессов;
- динамическое подключение модулей, содержащих описание исследуемых процессов противоборства субъектов;
- разработка динамически подключаемых библиотек, содержащих описание исследуемых процессов противоборства субъектов.
Архитектура программного комплекса
Программный комплекс имеет модульную структуру. Логика работы программного комплекса состоит в динамическом подключении библиотеки, содержащей описание математической модели противоборства субъектов.
Модуль построения графиков отвечает за визуальное представление полученных результатов моделирования в виде настраиваемых графиков.
Аналитический модуль позволяет определить точки экстремума и области резких спадов/подъемов графиков исходя из заданных коэффициентов спада/подъема, а также отметить эти точки на графиках.
Модуль разработки библиотек, содержащих описание математических моделей противоборства субъектов, позволяет вводить все расчетные формулы математических моделей и создавать скомпилированный вариант библиотеки.
Главный модуль обеспечивает взаимодействие и совместную работу всех подключенных модулей, а так же предоставляет графический пользовательский интерфейс программного комплекса. Схематически архитектура программного комплекса представлена на рисунке 1.
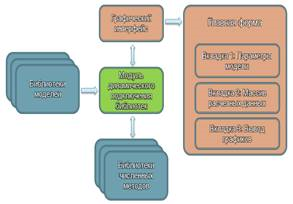
Рисунок 1 – Архитектура программного комплекса «Сфера»
Динамически подключаемые библиотеки математических моделей должны иметь определенную структуру, это необходимо для обеспечения правильного функционирования программного комплекса при работе с моделями, созданными сторонними разработчиками.
Описание программного комплекса
При первом запуске программного комплекса будет отображен экран с главным меню (см. рисунок 2), при последующих запусках будет отображено состояние последнего запуска.
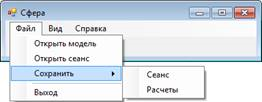
Рисунок 2 – Главное меню программного комплекса
Меню «Файл» содержит следующие пункты: «Открыть модель» – выбор динамической библиотеки модели для подключения; «Открыть сеанс» – выбор файла сохраненного сеанса работы; «Сохранить сеанс» – сохранение текущего сеанса работ в файл; «Сохранить расчеты» – сохранение текущих расчетов в файл. Меню «Вид» позволяет скрывать и показывать окна приложения.
В функциональном окне «Графики», показанном на рисунке 3, выполняется управление построением фазовых портретов и графиков динамики численности противоборствующих субъектов.
Описание окна «Графики» (рисунок 3): 1) выбор численного метода решения; 2) задание начального момента времени моделирования и шага времени; 3) компоненты управления временем моделирования; 4) компоненты управления масштабом области построения графиков; 5) область построения графиков; 6) выбор плоскости построения графиков; 7) настройка проведения серии вычислений с изменяемым параметром; 8) функция отображения стационарных точек; 9) выбор типа графика.
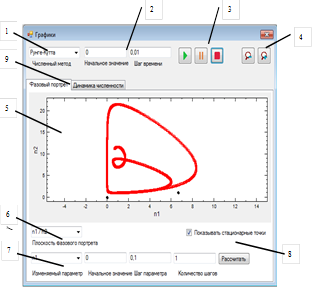 Рисунок 3 – Окно «Графики»
Рисунок 3 – Окно «Графики»
Основным окном управления параметрами моделирования является окно «Модель», которое состоит из следующих вкладок (см. рисунок 4): «Параметры» - позволяет осуществлять управление параметрами модели; «Стационарные точки» - отображает координаты стационарных точек и характер их устойчивости; «Описание» - отображает общие сведения о модели; «Условия» - позволяет настраивать поведение параметров, задавая определенные кусочно-линейные функции на различных временных промежутках.
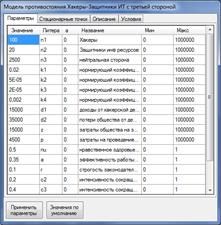
Рисунок 4 – Окно «Модель»
В окне «Графики» во вкладке «Динамика численности» отображаются результаты работы аналитического модуля по определению точек экстремума (см. рисунок 5) и областей резких спадов/подъемов графиков, которые выделяются специальными маркерами или линией.
Модуль разработки библиотек позволяет создавать различные математические модели противоборства субъектов без участия программиста. После разработки математической модели противоборства субъектов и определения всех расчетных формул необходимо последовательно добавить все параметры модели, затем уравнения системы дифференциальных уравнений и стационарные точки, затем произвести компиляцию данной модели в динамически подключаемую библиотеку.
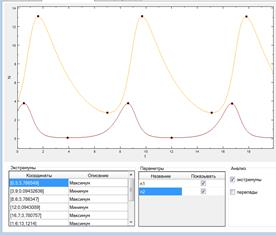
Рисунок 5 – Вкладка «Динамика численности» «Графики» (точки экстремума)
Заключение
Разработанный программный комплекс позволит: проводить моделирование процессов противоборства субъектов для различных прикладных задач и строить прогнозы состояния этого противоборства на интересующий интервал времени; отслеживать в динамике состояние противоборства субъектов, что позволит в пиковые интервалы времени службе безопасности быть в режиме повышенной готовности; обучать необходимое количество работников службы безопасности и не содержать «лишних»; проводить исследования по влиянию параметров модели на уровень противоборства субъектов в динамике с целью принятия решений по изменению стратегии защиты объекта; корректировать описание модели противоборства субъектов в соответствии с изменившимися условиями функционирования объекта защиты.
Библиографический список:
1. Свидетельство о государственной регистрации программы для ЭВМ от 29 июля 2010 года № 2010614978.
2. Вольтерра В. Математическая теория борьбы за существование /В. Вольтерра. - М.: ИКИ, 2004. – 288с.
3. Котенко И.В., Уланов А.В. Компьютерные войны в Интернете: моделирование противоборства программных агентов // Защита информации. Инсайд, № 4, 2007. С.38-45.
4. Гуц А.К., Коробицын В.В. Компьютерное моделирование этногенетических процессов. // Ученый совет мат. фак. ОмГУ. - Деп. в ВИНИТИ 24.09.97, N2903 B97. 23 c
5. Мудров А.Е. Численные методы для ПЭВМ на языках паскаль, Фортран и Бейсик. Томск: МП «Раско», 1991. – 285с.







