В данной работе решается задача сбора статистических данных при использовании программы, которая решает экономические задачи теории игр, сводя их к задачам линейного программирования (ЗЛП). Приводится теоретическая часть экономической интерпретации теории игр, описан алгоритм приведения задачи к ЗЛП. Анализируется использование прикладной программы для сбора математической статистики.
Ключевые слова: теория игр, экономические задачи, линейное программирование, математическая статистика.
1 Теория игр. Экономическая интерпретация.
Теорию игр чаще всего рассматривают как раздел математической экономики, изучающий решение конфликтов между игроками и оптимальность их стратегий. Конфликт может относиться к разным областям человеческого интереса: чаще всего это экономика, социология, политология. В данной работе рассматривается как раз область экономики.
В данном случае целью теории игр является выработка рекомендаций или нахождение конкретных решений для различного поведения конкурентов (игроков) в конфликтной ситуации (игре), т. е. выбор оптимальной стратегии для каждого из них. Игровая модель, в отличие от конфликтной ситуации, строится по определенным законам, а игроки придерживаются определенных правил.
Решение экономической игры сводится к получению результатов, которые показывают в каком соотношении нужно выбирать тактику для получения наибольшей выгоды или набор тактик, которые нужно выполнять одновременно. Для более точного прогнозирования прибыли (убытков) следует так же вести статистику и на основе полученных данных делать анализ.
2 Общая теория матричных игр. Алгоритм.
Описание игры включает перечень игроков, множество возможных их действий и оценки эффективности этих действий для каждого из игроков. Преимущество представления игры в виде матрицы заключается в хорошей наглядности.
Все возможные исходы игры сводятся в таблицу (табл. 1), которую принято называть платежной матрицей. Строки таблицы соответствуют различным стратегиям первого игрока, а столбцы — стратегиям второго игрока. ![]() называется выигрыш первого игрока.
называется выигрыш первого игрока.
Выбор действия называют выбором стратегии игрока. Если каждый игрок может выбрать только одно из конечного множества своих действий, то это называется решением игры в чистых стратегиях, иначе — решением игры в смешанных стратегиях.
Проверкой игры на решение в чистых (смешанных) стратегиях является проверка на наличие седловой точки. В играх с нулевой суммой седловая точка платёжной матрицы является равновесием Нэша. Таким образом, если седловая точка была определена, то решение находится в чистых стратегиях и наоборот.
Для нахождения седловой точки нужно найти минимальный элемент в каждой строке и максимальный в каждом столбце. Далее найти ![]() — максимальный из минимальных и
— максимальный из минимальных и ![]() — минимальный из максимальных элементов. Первое значение является нижней ценой игры и минимальным гарантированным выигрышем первого игрока, второе — верхней ценой игры и максимальным значением проигрыша второго игрока. Если нижняя и верхняя границы совпадают — это значение является седловой точкой и, соответственно, ценой игры т. е. первый игрок получит максимальную выгоду, равную этому значению, а второй проиграет не больше этого значения.
— минимальный из максимальных элементов. Первое значение является нижней ценой игры и минимальным гарантированным выигрышем первого игрока, второе — верхней ценой игры и максимальным значением проигрыша второго игрока. Если нижняя и верхняя границы совпадают — это значение является седловой точкой и, соответственно, ценой игры т. е. первый игрок получит максимальную выгоду, равную этому значению, а второй проиграет не больше этого значения.
При условии, что седловая точка не была найдена, решение ищется в смешанных стратегиях. Смешанной стратегией первого игрока называется вектор ![]() , где m — количество строк, все
, где m — количество строк, все ![]() и
и ![]() . При этом
. При этом ![]() – вероятность, с которой первый игрок выбирает свою i-ю стратегию. Аналогично определяется смешанная стратегия второго игрока. Чистая стратегия также подпадает под определение смешанной — в этом случае все вероятности равны нулю, кроме одной, равной единице.
– вероятность, с которой первый игрок выбирает свою i-ю стратегию. Аналогично определяется смешанная стратегия второго игрока. Чистая стратегия также подпадает под определение смешанной — в этом случае все вероятности равны нулю, кроме одной, равной единице.
Таблица 1
Платежная матрица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для начала определяется седловая точка. Считаем, что первый игрок выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а второй игрок выбирает свою стратегию так, чтобы минимизировать выигрыш первого игрока. Находим гарантированный выигрыш, определяемый нижней ценой игры ![]() . Верхняя цена игры
. Верхняя цена игры ![]() . Точка является седловой, если
. Точка является седловой, если ![]() . Если такая точка была найдена, то выписывается решение в чистых стратегиях. Иначе цена игры находится в промежутке
. Если такая точка была найдена, то выписывается решение в чистых стратегиях. Иначе цена игры находится в промежутке ![]() и решение игры находится в смешанных стратегиях.
и решение игры находится в смешанных стратегиях.
Для решения игры в смешанных стратегиях рассмотрим задачу отыскивания оптимальной стратегии второго игрока по ПМ из таблицы 1.
Цена игры v неизвестна, однако можно считать, что ![]() . Последнее условие выполняется всегда, если все элементы ПМ неотрицательны, а этого можно достигнуть, прибавив ко всем элементам матрицы минимальный элемент в ней. Будем считать, что
. Последнее условие выполняется всегда, если все элементы ПМ неотрицательны, а этого можно достигнуть, прибавив ко всем элементам матрицы минимальный элемент в ней. Будем считать, что ![]() .
.
Таблица 2
Преобразованная платежная матрица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Целевая функция имеет вид:
Ограничения ЗПЛ определяются по формулам:
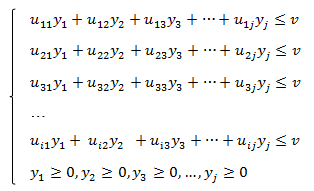 (2)
(2)
Преобразуем систему ограничений 2, разделив все члены неравенства на v.
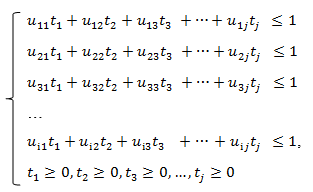 (3)
(3)
где ![]()
По условию ![]() , разделим обе части на v и получим новую целевую функцию:
, разделим обе части на v и получим новую целевую функцию: ![]() (4)
(4)
Оптимальная стратегия ![]() игрока 2 должна минимизировать величину v, следовательно, функция
игрока 2 должна минимизировать величину v, следовательно, функция ![]() должна принимать максимальное значение.
должна принимать максимальное значение.
Получена задача линейного программирования: найти максимум целевой функции (4) при ограничениях (3).
Решаем задачу симплекс-методом и получаем значения ![]() . Цена игры находится по формуле:
. Цена игры находится по формуле: ![]() , а вероятности использования тактик игроком 2 по формуле:
, а вероятности использования тактик игроком 2 по формуле: ![]() .
.
Из таблицы, в которой содержатся значения последней итерации симплекс-метода, можно получить значения решения двойственной задачи ![]() . Эти значения являются значениями в столбцах добавочных переменных в последней строке. Для нахождения вероятности использования тактик игрока 1 применяем формулу:
. Эти значения являются значениями в столбцах добавочных переменных в последней строке. Для нахождения вероятности использования тактик игрока 1 применяем формулу: ![]() . Так как мы преобразовывали матрицу, то следует отнять от цены игры минимальный элемент:
. Так как мы преобразовывали матрицу, то следует отнять от цены игры минимальный элемент: ![]() .
.
В итоге получим решение матричной игры в смешанных стратегиях:
Данный метод решения подходит для всех матричных игр для двух игроков с неограниченным количеством стратегий игроков.
4 Прикладная программа
Данная программа была написана в интегрированной среде разработки MS Visual Studio 2017 с использованием языка c# и платформы.NET Framework, выполняющая 9 различных функций. Интерфейс и пример решения показан на рис. 1.
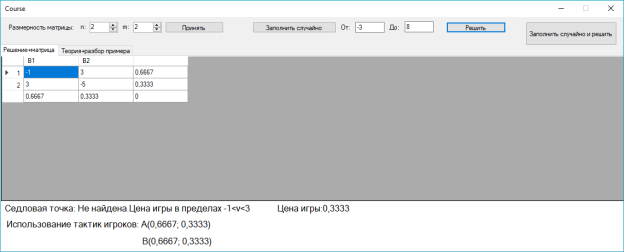
Рис. 1. Демонстрация интерфейса и решения с помощью прикладной программы
Рассмотрим пример решения задачи: швейное предприятие, выпускающее детские платья и костюмы, реализует свою продукцию через фирменный магазин. Сбыт продукции зависит от состояния погоды. Но данным прошлых наблюдений предприятие в течении апреля — мая в условиях теплой погоды может реализовать 600 костюмов и 1975 платьев, а при прохладной погоде 1000 костюмов и 625 платьев. Известно, что затраты на единицу продукции в течение указанных месяцев составили для костюмов 27 руб., для платьев 8 руб., а цена реализации равна соответственно 48 руб. и 16 руб.
Предприятие располагает в этих условиях двумя стратегиями: стратегия ![]() — в расчете на теплую погоду и стратегия
— в расчете на теплую погоду и стратегия ![]() — в расчете на холодную погоду. Природу будим рассматривать как второго игрока также с двумя стратегиями: прохладная погода (
— в расчете на холодную погоду. Природу будим рассматривать как второго игрока также с двумя стратегиями: прохладная погода (![]() ) и теплая погода (
) и теплая погода (![]() ).
).
Если предприятие выберет стратегию ![]() , то в случае прохладной погоды (
, то в случае прохладной погоды (![]() ) доход составит: 6 800 руб., а в случае теплой погоды (
) доход составит: 6 800 руб., а в случае теплой погоды (![]() ) доход равен 28 400 руб.
) доход равен 28 400 руб.
Если предприятие выберет стратегию ![]() , то реализация продукции в условиях прохладной погоды даст доход 26 000 руб., а в условиях теплой погоды 6 800.
, то реализация продукции в условиях прохладной погоды даст доход 26 000 руб., а в условиях теплой погоды 6 800.
Таблица 3
Условие задачи. Платежная матрица
|
|
|
|
|
|
6800 |
28400 |
|
|
26000 |
6800 |
Внесем условие задачи в прикладную программу и найдем решение (рис. 2).
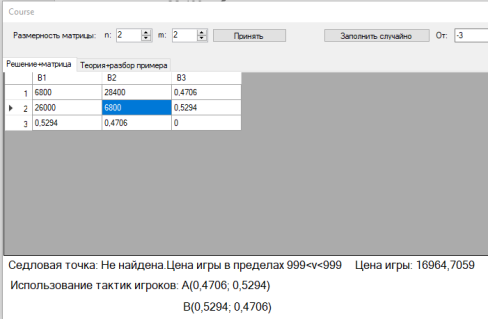
Рис. 2. Решение задачи
Таким образом получаем, что с вероятностью 53 % будет прохладная погода, а 47 % — тёплая. Таким образом швейному предприятию стоит выпускать 47 % продукции в расчете на теплую погоду, а 53 % продукции — с расчетом на прохладную погоду, от общего количества реализованной продукции за период, чтобы получить среднюю прибыль в размере 16964руб.
Найдем решения случайно заполненных платежных матриц при разных значениях размерности и диапазона значений случайного заполнения.
Таблица 4
Зависимость частоты присутствия седловой точки от диапазона случайного заполнения иразмерности матрицы
|
Размерность матрицы Диапазон значений |
3*3 |
6*6 |
9*9 |
|
3 |
27 |
8 |
6 |
|
7 |
25 |
5 |
4 |
|
10 |
21 |
0 |
2 |
|
15 |
20 |
1 |
0 |
|
20 |
14 |
2 |
0 |
|
30 |
13 |
0 |
0 |
|
40 |
18 |
1 |
0 |
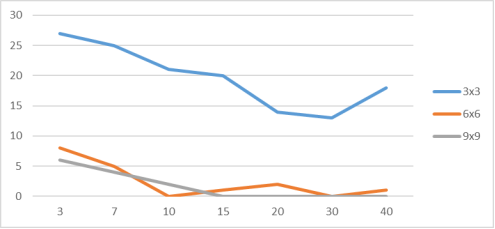
Рис. 3. Графики зависимости частоты присутствия седловой точки от диапазона случайного заполнения
Данные из таблицы 4 и рис. 3 наглядно демонстрируют, что данную прикладную программу можно использовать в целях сбора статистических данных о проведении ряда экспериментов со случайными значениями. Так, например, в матрице размерностью 3*3 за 7 экспериментов средний процент присутствия седловой сточки составляет 39,4 %. Также можно заметит, что процент присутствия седловой точки уменьшается с увеличением диапазона допустимых значений. В итоге для задач, где количество допустимых стратегий игроков меньше, соответственно больший шанс выбора единственно верной тактики.
Анализ полученных результатов при решении задач и тестовых прогонов прикладной программы показывает, что программа в полной мере справляется с поставленной задачей и выполняет все реализованные функции.
Данная система прошла все проверки и находится в полностью работоспособном состоянии. Дальнейшая разработка связана с расширением функционала программы.
Литература:
- Д. Кнут «Искусство программирования. Том 1. Основные алгоритмы» 2015г. 720стр. Издательство: Вильямс.
- Романьков, В А Введение В Теорию Игр: Учебное Пособие / Романьков В А. — Москва: ИЛ, 2016. — 834 cтр.
- Рейзлин В. И. Численные методы оптимизации: Учебное пособие / Погребной В. К. — Томск: НИ ПТУ, 2013. — 103стр.
- Ашманов С. А. Линейное программирование. М.: Наука. 1981.
- Орлов А. И. Теория принятия решений Учебное пособие. — М.: Издательство «Март», 2004.
- Зиборов, В. В. Visual C# 2012 на примерах / В. В. Зиборов. — М.: БХВ-Петербург, 2013. — 480с.







