Профессиональное становление обучающихся средних профессиональных заведений происходит в процессе изучения учебных и специальных дисциплин, в разнообразии видов их деятельности. Особая роль отводится дисциплине «Физика». Статья посвящена рассмотрению вопроса о роли решения физических задач в реализации развивающей функции обучения.
Ключевые слова: физическая теория, развивающее обучение, физическая задача.
Учебная дисциплина «Физика» является основой для изучения студентами средних профессиональных заведений специальных дисциплин и последующей профессиональной деятельности. При учении физики большое значение имеет практическое применение теоретических знаний, главное из которых — умение решать задачи.
В ходе решения задач у обучающихся вырабатываются приемы и навыки решения на основе общего подхода, помогающие им в дальнейшем решать производственные задачи.
В общем алгоритме решения задачи можно выделить три этапа. Наиболее содержательный этап решения задачи — это физический этап — этап осмысления проблемы, изложенной в задаче, и составление замкнутой системы уравнений с учетом связей и отношений в физической системе и используемых идеализации; математический этап — этап решения системы уравнений и расчет численного значения искомой величины; и последний этап — этап формирования результата решения задачи.
Следует заметить, что любая частная физическая задача представляет собой дедуктивно выстроенную последовательность рассуждений от фундаментального ядра физической теории к теоретическому следствию. В обычных текстовых задачах, которые решает обучающийся, содержательно отражается гипотетико-дедуктивная модель организации знания физической теории. Реализуемый при решении задачи предоставленный алгоритм отражает в динамике мыслительных операций такую организацию знания.
Средством решения задачи, безусловно, является физическая теория, но знание теории не является непосредственным гарантом умений решать задачи [1]. В этой связи важным является формирование знаний об обобщенных приемах действий, осознание обучающимися операционного состава умственных действий на каждом этапе решения физической задачи.
На физическом этапе решения задачи осуществляется: 1) уяснение сущности физического процесса, сформулированного в задаче; 2) анализ условий протекания процесса, сформулированных в задаче; 3) вычленение связей и отношений в физической системе, используемых идеализаций; 4) выявление возможности использования тех или иных фундаментальных законов с целью составления математической модели задачи в виде замкнутой системы уравнений; 5) составление математической модели-задачи, т. е. собственно замкнутой системы уравнений.
На последнем этапе — этапе формирования результата решения — осуществляются такие действия, как: 1) анализ связи искомой величины с другими динамическими переменными; 2) анализ условий и границы существования полученной зависимости; 3) выявление возможности модификации проблемы при других условиях и в других физических системах; 4) оценка правдоподобия полученного численного значения.
При анализе исходных данных и результатов решения важно отметить предсказательную функцию физической теории. Решение физической задачи является яркой иллюстрацией гносеологической функции физической теории. Успех в решении задачи определяется ясной формулировкой и соответствующей адекватной формализацией начального состояния и условий протекания описываемого физического явления [2].
Особые затруднения у обучающихся вызывают задачи, в условиях которых «ничего не дано» [3], то есть отсутствуют определенные физические величины. Такие задачи не содержат подсказок для решения, но именно такие задачи способствуют реализации развивающей функции обучения, так как требуют умений анализировать, моделировать, сравнивать. При решении таких задач вначале надо по возможности определить, от каких физических величин может зависеть ответ задачи. Далее попытаться записать уравнения, в которые входит искомая величина. Затем проанализировать полученные уравнения, здесь не всегда стоит добиваться, чтобы число уравнений совпадало с числом неизвестных. Рассмотрим примеры таких задач.
Задача 1. Насколько повысится внутренняя энергия воздуха в комнате, если в ней протопить печь?
Решение. Давление р в комнате в связи с ее негерметичностью не изменяется.
Значит, при повышении температуры Т часть воздуха выходит наружу. Так как объем комнаты постоянен, то
![]()
Внутренняя энергия U идеального газа пропорциональна величине
![]() (
(![]() , следовательно,
, следовательно, ![]() , т. е. внутренняя энергия не изменится.
, т. е. внутренняя энергия не изменится.
Задача 2. Тепловой цикл, проводимый с одноатомным идеальным газом, состоит из двух изохор и двух изобар. Найти максимальный КПД цикла.
Решение. Коэффициент полезного действия цикла ![]() . Найдем A и Q.
. Найдем A и Q.
Газ получает количество теплоты на участках 1–2 и 2–3 (рис.1)
По первому закону термодинамики полученное количество теплоты связано с изменением внутренней энергии газа и совершенной работой уравнением:
![]() .
.
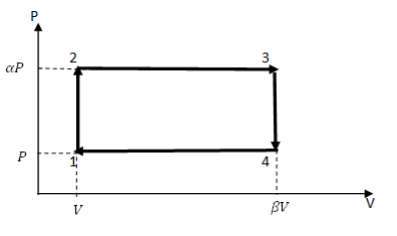
Рис. 1
Пусть в изохорном процессе 1–2 давление увеличилось в α раз, а в изобарном процессе 2–3 объем газа увеличился в β раз. Тогда
![]()
Работа ![]() равна
равна
![]()
Подставляя выражение для ![]() и
и ![]() в первый закон термодинамики, получим:
в первый закон термодинамики, получим:
![]() [3/2 (αβ-1)+α(β-1)]pV.
[3/2 (αβ-1)+α(β-1)]pV.
Работа в цикле 1–2–3–4 равна
A=(α-1) (β-1) pV.
Коэффициент полезного действия цикла равен
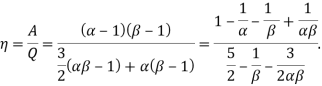
КПД растет при увеличении α и β, и его максимальное значение (при очень больших α и β) равно ![]() =40 %.
=40 %.
Таким образом, получился численный результат при полном «отсутствии» начальных данных.
Чтобы научить обучающихся решать подобные задачи, следует выделить основные этапы их решения. В качестве пропедевтики важно рассматривать больше качественных задач, делая акцент на разных взаимосвязях физических величин.
Таким образом, в ходе решения физических задач, в которых «ничего не дано» отрабатываются приемы и навыки решения на основе общего подхода, развивается теоретическое мышление, помогающие обучающимся средних профессиональных заведений в дальнейшем решать производственные задачи.
Литература:
- Низамов, И. М. Методологические основы формирования практических умений школьников в процессе решения физических задач [Текст]: автореф. дис. … докт. пед. наук / И. М. Низамов. — М.: Просвещение, 1990. — 36с.
- Половникова, Л. Б. Развитие теоретического мышления студентов технического вуза в процессе решения физических задач [Текст] /Л. Б. Половникова // Вестник Московского государственного областного университета. Серия «Педагогика». — № 4. — М.: Изд-во МГОУ, 2009. — С.131–135.
- Спажакин В. А. Задачи, в которых «ничего не дано» [Текст] /В. А. Спажакин //Физика в школе. — № 6–М.: «Школа-Пресс», 1997.– С.66–68







