В данной статье представлены механизмы образования дефектов в хрупком упругом материале, которые влияют на его качество.
Ключевые слова: кремний, механическая прочность, остаточные напряжения, дислокации, микровключения, трещины.
В современной промышленности одним из наиболее часто используемых материалов являются пластины кремния. Приборы, изготовленные на пластинах кремния, применяются в различных отраслях, в том числе в силовой электронике, космической отрасли, автомобилестроения и других. Надежность изделий на основе пластин кремния зависит от их качества. На качество кремниевых пластин влияет механическая прочность и возникающие при этом остаточные напряжения. А механическая прочность в свою очередь зависит от поверхностных и внутренних дефектов — трещины, микровключения и дислокации.
К первым работам, посвященным распространению трещин в деформируемом твердом теле, относятся работы Гриффитса. В результате развития идей об учете сил межчастичного сцепления тупиковой части трещины Гриффитс сформулировал энергетический метод определения предельно равновесного состояния хрупкого тела с трещиной. Так же впервые вывел формулу решения задачи о разрушающей или предельной нагрузке ![]() для тела с изолированной прямолинейной трещиной.
для тела с изолированной прямолинейной трещиной.
![]() (1)
(1)
где ![]() — модуль Юнга,
— модуль Юнга, ![]() — плотность эффективной поверхности энергии материалов,
— плотность эффективной поверхности энергии материалов, ![]() — длина трещины.
— длина трещины.
Работы Гриффитса стали основополагающими для дальнейших исследований. Так, Смекал попытался объяснить причины большого расхождения между наблюдаемой (технической) прочностью макроскопических твердых тел и их теоретической прочностью из-за наличия в твердом теле дефектов типа трещин. Кроме этого, Сак применил энергетический метод Гриффитса для решения пространственной задачи о разрушении хрупкого тела, ослабленного макроскопической доскообразной трещиной, когда тело подвергнуто на бесконечности растяжению полем однородных напряжений ![]() направленных перпендикулярно к плоскости трещины. Сак, вычислив упругую энергию
направленных перпендикулярно к плоскости трещины. Сак, вычислив упругую энергию ![]() трещины при действии напряжений
трещины при действии напряжений ![]() и применив энергетический принцип Гриффитса, установил формулу для определения значений предельных напряжений:
и применив энергетический принцип Гриффитса, установил формулу для определения значений предельных напряжений:
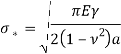 , (2)
, (2)
где ![]() — радиус трещины,
— радиус трещины, ![]() — коэффициент Пуассона.
— коэффициент Пуассона.
Задачи Гриффитса и Сака затем были рассмотрены Эллиотом без привлечения энергетической теории. В этой работе кроме вычисления предельных значений автором была сделана попытка определить структуру края трещины. При решении задач о распространении трещин в деформируемом теле Эллиот неоправданно пренебрег силами межчастичного притяжения между берегами развивающейся трещины по всей ее поверхности. Расстояние между берегами тупиковой части раскрывающейся трещины соизмеримо с межатомным расстоянием, поэтому в этой части трещины действуют еще силы межчастичного сцепления достаточной величины, которые должны быть учтены при рассмотрении предельно равновесного состояния тела.
На равновесии хрупких тел, ослабленных трещинами, существенное влияние оказывают силы межчастичного сцепления. Поэтому в своих работах Г. И. Баренблатт уточнил и дополнил постановку задач о равновесных макротрещинах хрупкого разрушения и предложил новую теоретическую схему решения задач деформируемого тела. Эта схема основана на следующих гипотезах:
1. Ширина ![]() концевой области трещины, то есть области, в которой значительные силы межчастичного сцепления, мала по сравнению с размерами всей трещины (рис.1). Эта гипотеза, по существу, определяет класс рассматриваемых трещин, так как к некоторым микротрещинам эта гипотеза неприменима.
концевой области трещины, то есть области, в которой значительные силы межчастичного сцепления, мала по сравнению с размерами всей трещины (рис.1). Эта гипотеза, по существу, определяет класс рассматриваемых трещин, так как к некоторым микротрещинам эта гипотеза неприменима.
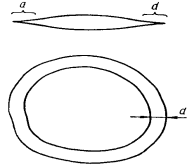
Рис. 1. Ширина концевой области трещин
2. Форма нормального сечения поверхности трещины в концевой области (локальное распределение сил сцепления по поверхности трещин) не зависит от действующих нагрузок и для данного материала при данных условиях (температура, состав и давление окружающей атмосферы и т.д) и всегда одинакова. Под нормальным сечением следует понимать сечение плоскостью нормальной по отношению к контуру трещины. Область тупиковой (концевой) части трещины при ее распространении должна перемещаться поступательно, сохраняя свою начальную форму.
Эта гипотеза получила название автономности концевой области трещин. Гипотеза и опирающиеся на нее выводы применимы только для исследования подвижно-равновесного состояния трещины в деформируемом твердом теле и определения предельной нагрузки.
3. Противоположные берега трещин на ее кромках плавно смыкаются или напряжения в тупиковой части (в конце) трещины конечны.
Данные гипотезы упрощают анализ равновесного состояния хрупкого тела с макротрещинами (с точки зрения определения предельных нагрузок для заданной конфигурации трещин) и позволяет сформулировать новые положения теории распространения трещин.
Техническая прочность реальных макроскопических твердых тел отличается от теоретической (на два — три порядка ниже) из-за наличия дефектов структуры реальных макроскопических тел. В структуре реальных твердых тел, которые, как правило, неоднородны, всегда имеются различные дефекты: скопления дислокаций или вакансий, границы блоков или зерен, различные включения, поры, трещины и т. п. Дефекты возникают при образовании твердого тела из жидкого состояния и в процессе его деформации. Из-за неоднородности материала в областях, где расположены дефекты, происходит концентрация внутренних напряжений, в результате чего в отдельных областях тела внутренние напряжения достигают величины теоретической прочности, хотя средние значения напряжений сравнительно малы. Это приводит к тому, что в перенапряженных областях деформируемого твердого тела образуются мельчайшие трещины (локальное разрушение).
Прочностные свойства реальных твердых тел существенно зависят от напряженно-деформированного состояния в тех областях, где деформации превосходят предел упругости. Следовательно, к таким областям тела классическая модель теории упругости неприменима. В связи с этим для разработки элементов количественной теории прочности реальных твердых тел, в частности для решения задач о распространении трещин в деформируемом хрупком теле, модель упругой среды необходимо дополнить некоторыми новыми свойствами, т. е. требуется сформулировать новую расчетную модель.
Согласно такой расчетной модели хрупкого тела, которую сформулировал Панасюк В. В., в процессе деформации твердого тела, ослабленного трещинами или другими дефектами такого типа, в некоторых его областях (например, вблизи острия трещины) возникают деформации, превосходящие предел упругости, т. е. в теле появляются прослойки (области), в которых не выполняются условия закона Гука. В хрупких материалах такие области представляют собой малые объемы (прослойки) по сравнению с той частью тела, которая деформируется упруго. Учитывая это, реальное твердое тело, деформируемое системой внешних сил, будем рассматривать как некоторое сплошное упругое тело (материальный континуум), деформируемое упруго всюду, кроме некоторых прослоек материала, в которых деформации тела превосходят предел упругости. Такие «перенапряженные» прослойки тела, где материал деформируется за пределом упругости, можно мысленно удалить из тела, образовав, таким образом, в теле некоторые щели — трещины, к поверхностям которых приложены напряжения, соответствующие действию удаленного материала.
В связи с этим прежде всего необходимо выяснить зависимость между силами и деформациями в той части деформируемого тела, где деформации превосходят предел упругости. В общем случае решение такой задачи наталкивается на большие трудности. Однако при исследовании задач о предельно равновесном состоянии хрупких тел, ослабленных трещинами, приближенное определение сил взаимодействия между берегами трещины оказывается возможным.
Пусть хрупкое тело, ослабленное трещиной, подвергнуто растяжению системой внешних сил. Тогда при сколь угодно малой, но не равной нулю, внешней нагрузке в окрестности острия трещины возникнут деформации, превосходящие предел упругости. Такие области тела рассматривают как мельчайшие трещины, т. е. трещины, противоположные берега которых взаимодействуют между собой. Так как рассматриваемое тело хрупкое, то силы взаимодействия (притяжения между берегами мельчайших трещин) определяются интенсивностью межчастичных сил сцепления ![]() при
при![]() , где
, где ![]() — расстояние между берегами трещин. Поскольку силы
— расстояние между берегами трещин. Поскольку силы ![]() при
при ![]() изучены неполно, то, основываясь на описанных выше общих свойствах функции
изучены неполно, то, основываясь на описанных выше общих свойствах функции ![]() и имея в виду макроскопическую упругую модель, можно ввести следующую гипотезу.
и имея в виду макроскопическую упругую модель, можно ввести следующую гипотезу.
Для идеально хрупкого тела в рамках модели сплошной среды силы ослабленных межчастичных связей ![]() при
при ![]() определяются так: если расстояние между берегами трещины не превосходит некоторой величины
определяются так: если расстояние между берегами трещины не превосходит некоторой величины ![]() (постоянной для данного материала при заданных условиях), они равны постоянной величине
(постоянной для данного материала при заданных условиях), они равны постоянной величине ![]() ; если же расстояние между берегами трещины больше величины
; если же расстояние между берегами трещины больше величины ![]() силы притяжения между ними равны нулю.
силы притяжения между ними равны нулю.
Согласно формуле 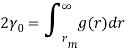 значения
значения ![]() связаны между собой равенством:
связаны между собой равенством:
![]()
где ![]() — предел хрупкой прочности данного материала,
— предел хрупкой прочности данного материала, ![]() — критический интервал.
— критический интервал.
Таким образом, расчетная модель реального хрупкого тела представляет собой сплошное упругое тело, которое характеризуется следующими свойствами:
-
Максимальные растягивающие напряжения, возникающие в таком теле, не превосходят величины
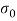 — предела хрупкой прочности материала;
— предела хрупкой прочности материала;
-
Зависимость между напряжениями и деформациями выражается законом Гука, если растягивающие напряжения не достигают величины
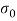 ;
;
-
В теле образуются микротрещины (области ослабленных межчастичных связей), если максимальные растягивающие напряжения, которые вычислены на основе линейной теории упругости, достигают величины
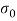 ;
;
-
Противоположные берега таких микротрещин притягиваются с напряжением
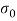 , если расстояние между берегами микротрещины не превышает величины
, если расстояние между берегами микротрещины не превышает величины 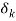 , и не взаимодействуют между собой, если расстояние больше
, и не взаимодействуют между собой, если расстояние больше 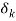 .
.
Описанная выше модель хрупкого тела с трещинами (![]() - модель) определяется помимо упругих коэффициентов (закон Гука) еще двумя характеристиками: пределом хрупкой прочности
- модель) определяется помимо упругих коэффициентов (закон Гука) еще двумя характеристиками: пределом хрупкой прочности ![]() и критическим интервалом
и критическим интервалом ![]() В рамках этой модели сформулирована общая задача возникновения и развития (распространения) трещин в реальном хрупком теле, как соответствующая силовая задача статистики деформируемого упругого тела.
В рамках этой модели сформулирована общая задача возникновения и развития (распространения) трещин в реальном хрупком теле, как соответствующая силовая задача статистики деформируемого упругого тела.
В рамках данной модели трещина в реальном твердом теле представляется в виде разреза. Область трещины, где расстояние между ее берегами превосходит величину ![]() (область разорванных межчастичных связей), соответствует участка разреза, противоположные берега которого не взаимодействуют друг с другом. Тупиковые участки трещины — область тела, где материал деформирован за пределами упругости (области ослабления межчастичных связей) соответствует в
(область разорванных межчастичных связей), соответствует участка разреза, противоположные берега которого не взаимодействуют друг с другом. Тупиковые участки трещины — область тела, где материал деформирован за пределами упругости (области ослабления межчастичных связей) соответствует в ![]() -модели разрезам, противоположные берега которых притягиваются с напряжением
-модели разрезам, противоположные берега которых притягиваются с напряжением ![]() , пока расстояние между ними меньше
, пока расстояние между ними меньше ![]() Следовательно, развитие хрупкого разрушения или, другими словами, распространение реальной трещины в
Следовательно, развитие хрупкого разрушения или, другими словами, распространение реальной трещины в ![]() -модели определяется процессом перехода точек области ослабленных межчастичных связей в область разорванных связей. Таким образом, распространение реальной трещины в деформируемом твердом теле можно записать так:
-модели определяется процессом перехода точек области ослабленных межчастичных связей в область разорванных связей. Таким образом, распространение реальной трещины в деформируемом твердом теле можно записать так:
![]()
где
Рис. 2. Схема трещины в деформируемом твердом теле
Наименьшее значение внешней нагрузке ![]() для хрупкого тела с трещинами, при достижении которого достигается условие (3) и наступает возможность распространения трещины, называется предельной нагрузкой. Если выполняется это условие в одной точке тупиковой части начальной трещины, то такая начальная трещина называется предельно равновесной.
для хрупкого тела с трещинами, при достижении которого достигается условие (3) и наступает возможность распространения трещины, называется предельной нагрузкой. Если выполняется это условие в одной точке тупиковой части начальной трещины, то такая начальная трещина называется предельно равновесной.
Можно сделать следующий вывод: изучение распространения трещин в деформируемом хрупком теле при монотонно возрастающей внешней нагрузке в этом случае сводится к решению задачи линейной теории упругости в рамках сформулированной расчетной модели и определению параметров внешней нагрузки, удовлетворяющим условию ![]()
Наряду с поверхностными дефектами кремниевые пластины имеют остаточные напряжения, которые обусловлены технологией выращивания кремниевого слитка, а также технологическими операциями их обработки. В данном случае рассматриваются напряжения I рода (макронапряжения).
Механические напряжения в кремниевых пластинах, причем значительные, возникают на первых стадиях технологического процесса изготовления пластин (резка слитка на пластины, операции шлифования и полирования). Пластины со значительными остаточными напряжениями будут иметь низкую механическую прочность, и, следовательно, могут разрушиться при последующих технологических операциях (диффузии, окислении, эпитаксии и т. д.), поскольку они приводят к появлению дополнительных остаточных напряжений.
Процессы диффузии, окисления, эпитаксии обычно проводятся при высоких температурах. Диффузия примесей в кремний может сопровождаться короблением пластин. Механические напряжения появляются из-за изменения постоянной решетки и поверхностного натяжения в результате легирования. В связи с этим, особый интерес представляет диффузия фосфора (свыше ![]() ). Это обусловлено тем, что величина и направление прогиба пластин зависят от условий охлаждения. При медленном охлаждении прогиб пластин происходит в другом направлении, чем при быстром охлаждении. Это явление качественно можно объяснить следующим образом. В легированной фосфором части пластины изменяется постоянная кристаллической решетки. Она становиться меньше, чем в нелегированной части пластины. В слое с диффузионным фосфором возникают внутренние напряжения, приводящие к деформации (рис. 3.1).
). Это обусловлено тем, что величина и направление прогиба пластин зависят от условий охлаждения. При медленном охлаждении прогиб пластин происходит в другом направлении, чем при быстром охлаждении. Это явление качественно можно объяснить следующим образом. В легированной фосфором части пластины изменяется постоянная кристаллической решетки. Она становиться меньше, чем в нелегированной части пластины. В слое с диффузионным фосфором возникают внутренние напряжения, приводящие к деформации (рис. 3.1).
Рис. 3.1. Влияние диффузии фосфора на деформацию пластин кремния при напряжениях ниже критических
Если напряжения превысят критическое значение, то в плоскости скольжения образуются дислокации. По окончанию процесса диффузии фосфора кристаллическая решетка окажется деформированной, и пластина будет прогибаться (рис. 3.2).
Рис. 3.2. Влияние диффузии фосфора на деформацию пластин кремния при быстром охлаждении после образования дислокаций
Быстрое охлаждение кремниевых пластин с примесью фосфора до комнатной температуры приводит к тому, что перенасыщенный фосфор не успевает охладиться и остается закристилизованным в решетке в замещающем положении. В результате пластина прогибается (рис. 3.2).. При медленном охлаждении сверхнасыщенный фосфор начинает взаимодействовать, формируя вторую фазу. В данном случае диффундированный слой фосфора создает напряжения противоположного направления (рис. 3.3). Следовательно, для избежания коробления пластин во время диффузии необходимо уравновесить силы, обусловленные внедрением фосфора. Это можно достичь различными способами. Например, путем одновременного легирования с двух сторон или подбором скорости охлаждения.
Рис. 3.3. Влияние диффузии фосфора на деформацию пластин кремния при медленном охлаждении
Кислород является наиболее важной примесью с точки зрения влияния его на механические свойства кремния. Наиболее сильное влияние кислород оказывает на кристаллы, выращенные по методу Чохральского. Это обусловлено тем, что кристаллы по методу Чохральского, выращенные в кварцевом тигле, могут иметь концентрацию кислорода ![]() , что соответствуем максимальной растворимости кислорода при температуре выращивания. В кристаллах, выращенных по методу зонной плавки, концентрация кислорода обычно не превышает
, что соответствуем максимальной растворимости кислорода при температуре выращивания. В кристаллах, выращенных по методу зонной плавки, концентрация кислорода обычно не превышает ![]() .
.
Предполагаются следующие механизмы, с помощью которых проявляется влияние твердого раствора кислорода:
- Взаимодействие атомов кислорода с дисклокациям;
- Взаимодействие макроскопических сгустков кислорода с дислокациями;
- Адсорбция (выпадение) кислорода вдоль линий дислокаций или в местах образования групп (ядер) дислокаций. Под влиянием механических напряжений дислокации могут перемещаться и размножаться по методу Франка-Рида.
Эффект закрепления дислокаций в зависимости от состояния кислорода имеет важное техническое значение. Возможно улучшение сопротивляемости пластины кремния к короблению. Однако до настоящего времени окончательно не установлено, какой кислород влияет на эффект закрепления дислокаций. Предполагается, что насыщенное состояние кислорода, а не его осадки влияют на эффект закрепления. Следует отметить, что при увеличении диаметра кремниевой пластины чувствительность пластины к короблению значительно возрастает, и соответственно проблема сопротивляемости материала к короблению принимает еще большее значение.
Как отмечалось выше, значительные остаточные напряжения возникают в кремниевых пластинах в результате механической обработки. В этой связи они будут иметь более низкую прочность и могут разрушиться при последующих операциях.
Литература:
- Казаков, О. Г. Проблема повышения качества кремниевых пластин/ О. Г. Казаков, А. А. Малаханов, А. В. Радьков//Энергетика, информатика, инновации — 2017 (электроэнергетика, электротехника и теплоэнергетика, математическое моделирование и информационные технологии в производстве). Сб. трудов VII-ой Межд. научн.-техн. конф. В 3т. Т1. — 2017– С. 94–97.
- Радькова Н. О. Повышение механической прочности кремниевых пластин путем снижения трещинообразования при их изготовлении: дис. … канд. техн. наук. Брянский государственный технический университет, Брянск, 2004.
- Sack, R. A. Extension of Griffith theory of rupture to three dimensions /R. A. Sack//Proc. Phys. Soc. — 1946. — № 58. — P. 729–736.
- Пансаюк, В. В. Предельное равновесие хрупких тел с трещинами /В. В. Панасюк. — Киев.: Наукова думка, 1968. — 246 с.
- Griffith, A. A. The phenomenon of rupture and flow in solids/A. A. Griffith//Phil. Trans. Roy. Soc. — 1920, ser. A. — 1920. –№ 221 — P. 163–198.







